2020年度　都立日比谷高校過去問【数学】大問４解説

問題ＰＤＦ
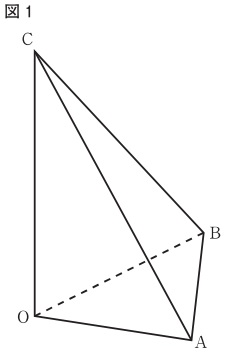
下の図１に示した立体ＯＡＢＣは、ＯＡ⊥ＯＢ、ＯＢ⊥ＯＣ、ＯＣ⊥ＯＡ、
ＯＡ＝ＯＢ＝６ｃｍ、ＯＣ＝８ｃｍの四面体である。

（１）
辺ＡＢの中点をＤとし、頂点Ｃと点Ｄを結び、線分ＣＤの中点をＥとし、
点Ｅから平面ＯＡＢに垂直な直線を引き、平面ＯＡＢとの交点をＦとし、
頂点Ｏと点Ｆを結んだ場合を考える。線分ＯＦの長さは何ｃｍか。

（２）
下の図２は、図１において、辺ＢＣ上にある点をＧとし、
頂点Ｏと点Ｇ、頂点Ａと点Ｇをそれぞれ結んだ場合を表している。
△ＯＡＧの面積が最も小さくなる場合の面積は何ｃｍ²か。

（３）
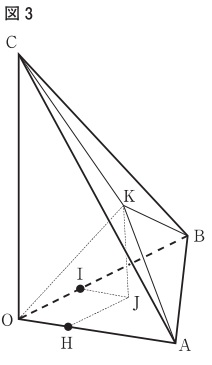
下の図３は、図１において、辺ＯＡ上にある点をＨ、
辺ＯＢ上にある点をＩとした場合を表している。
ＯＨ＝２ｃｍ、ＯＩ＝５/２ｃｍのとき、点Ｈを通り辺ＯＢに平行な直線と、
点Ｉを通り辺ＯＡに平行な直線との交点をＪとする。
点Ｊを通り、辺ＯＣに平行な直線と平面ＡＢＣとの交点をＫとし、
点Ｋと頂点Ｏ、点Ｋと頂点Ａ、点Ｋと頂点Ｂ、点Ｋと頂点Ｃをそれぞれ結ぶ。
四面体ＫＯＡＢの体積をＶｃｍ³、四面体ＫＯＡＣの体積をＷｃｍ³とする。
このとき、Ｖ：Ｗを最も簡単な整数の比で表せ。

＠解説＠
（１）

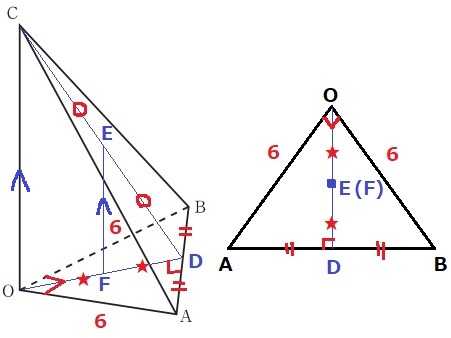
問題文に沿ってD、Ｅ、Ｆを図示する。
△ＣＯＤ∽△ＥＦＤで、ＣＥ：ＥＤ＝ＯＦ：ＦＤ＝１：１
ＯＦの長さはＯＤの半分。

△ＯＡＢは直角二等辺で、頂角Ｏと底辺ＡＢの中点Ｄを結んだ線分ＯＤは底辺ＡＢと直交する。
→△ＯＡＤも直角二等辺三角形
△ＯＡＤで三平方→１：１：√２より、ＯＤ＝６×１/√２＝３√２ｃｍ
よって、ＯＦ＝３√２÷２＝３√２/２ｃｍ

（２）
入試では解答だけでなく、答えを求める過程も記述する。

△ＯＡＧの面積が最小となるＧはどこだろう？
下側にありそうだが、Ｂに近づくほど面積が大きくなってしまう。

ポイントはＯＡ⊥ＯＢ、ＯＡ⊥ＯＣから、線分ＯＡ⊥面ＯＢＣであること。
ＯＧは面ＯＢＣ上にあるので、ＯＡ⊥ＯＧが成り立つ。
つまり、△ＯＡＧの底辺をＯＡとすると高さはＯＧとなり、
ＯＧが最も短くなるケースを考えればいい。

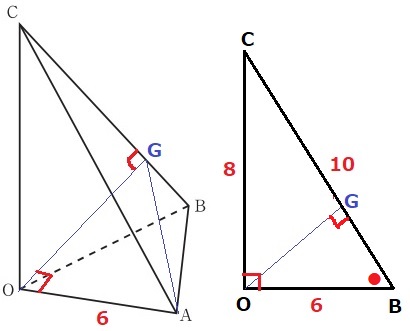
それはＯＧがＯとＢＣの距離、すなわち、ＯＧ⊥ＢＣのとき。
直角と共通角●→２角が等しく△ＢＯＣ∽△ＢＧＯ
△ＢＯＣの辺の比は３：４：５だから、ＯＧ＝６×４/５＝24/５ｃｍ
したがって、△ＯＡＧの面積は、６×24/５÷２＝72/５ｃｍ²

（３）

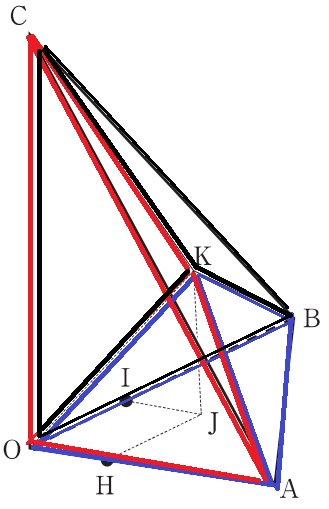
四面体をＫ－ＯＡＢ（Ｖ）、Ｋ－ＯＡＣ（Ｗ）、Ｋ－ＯＢＣに分割。

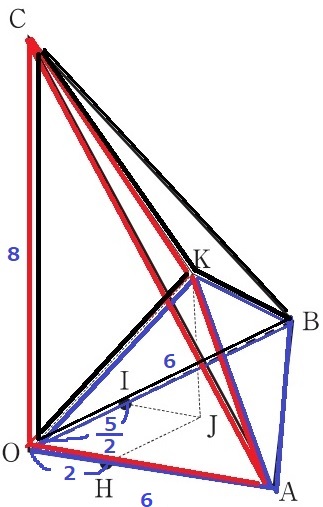
Ｋ－ＯＡＣ（Ｗ）…６×８÷２×５/２÷３＝20ｃｍ³
Ｋ－ＯＢＣ…底面積の△ＯＢＣの面積は、Ｋ－ＯＡＣの△ＯＡＣと同じ。
高さの比がＫ－ＯＡＣ：Ｋ－ＯＢＣ＝ＩＯ：ＨＯ＝５/２：２＝５：４なので、20×４/５＝16ｃｍ³
四面体（全体）…６×６÷２×８÷３＝48ｃｍ³
Ｋ－ＯＡＢ（Ｖ）…48－（20＋16）＝12ｃｍ³

したがって、Ｋ－ＯＡＢ（Ｖ）：Ｋ－ＯＡＣ（Ｗ）＝12：20＝３：５
ラストの問題なのにあっけなく終わったのは、王道の解き方ではないからか(;`ω´)?
国私立高校入試解説ページに戻る