問題ＰＤＦ
下図のような一辺の長さ12の正八面体ＡＢＣＤＥＦがあり、ＡＢ、ＡＣそれぞれの中点をＰ、Ｑとし、ＦＤ、ＦＥそれぞれを５：１に内分する点をＲ、Ｓとする。このとき、次の問に答えよ。
（１）
ＰＱの中点をＴ、ＲＳの中点をＵとするとき、ＴＵの長さを求めよ。
（２）
４点Ｐ、Ｑ、Ｒ、Ｓを通る平面で、この正八面体を切ったときの切り口の面積を求めよ。
＠解説＠
（１）
↑このＴＵを求める。
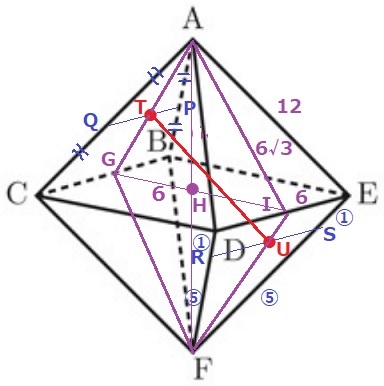
Ｔ、Ｕを通る断面で考えよう。
断面ＡＧＦＩは菱形で、対角線の交点をＨとする。
正八面体の各面は１辺12ｃｍの正方形→高さは６√３ｃｍ
四角形ＡＧＦＩは１辺６√３ｃｍの菱形である。
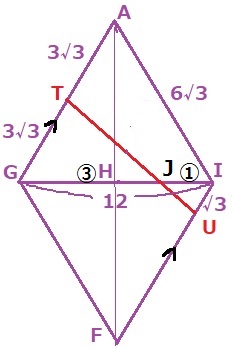
ＴＵが斜めで求めにくい(;´Д｀)
ＴＵよＧＩの交点をＪとする。
ＡＧ//ＩＦから、△ＴＧＪ∽△ＵＩＪ
相似比は、ＧＪ：ＪＩ＝ＴＧ：ＵＩ＝③：①
ＧＪ＝12×③/④＝９ｃｍ
ここで△ＡＧＨと△ＪＴＧに着目する。
共通角で、∠ＡＧＨ＝∠ＪＧＴ
ＧＨ：ＧＴ＝６：３√３＝２：√３
ＡＧ：ＪＧ＝６√３：９＝２√３：３＝２：√３
２辺の比とあいだの角が等しいから、△ＡＧＨ∽△ＪＴＧ
対応する角は等しいので、∠ＪＴＧ＝∠ＡＨＧ＝90°
△ＪＴＧで三平方→ＪＴ＝３√６ｃｍ
ＴＪ：ＪＵ＝３：１だから、ＴＵ＝３√６×４/３＝４√６ｃｍ
（２）
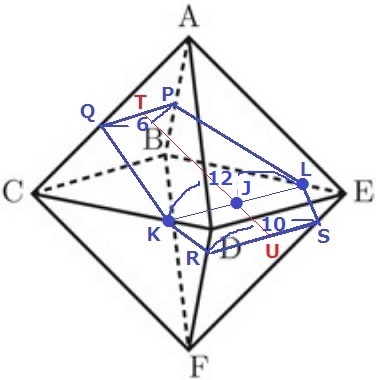
断面とＣＤ、ＢＥの交点をそれぞれＫ、Ｌとすると、
断面は六角形ＰＱＫＲＳＬとなる。
△ＡＢＣ∽△ＡＰＱより、ＰＱ＝６ｃｍ
△ＦＤＥ∽△ＦＲＳより、ＲＳ＝10ｃｍ
ＫＬ＝12
台形ＰＱＫＬと台形ＳＲＫＬの上底と下底がわかっている。
前問より、高さにあたるＴＪ：ＪＵ＝３：１
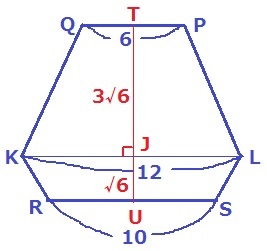
ＴＪ＝４√６×３/４＝３√６ｃｍ
ＪＵ＝４√６－３√６＝√６ｃｍ
台形ＰＱＫＬと台形ＳＲＫＬの面積を合計する。
＝（６＋12）×３√６÷２＋（12＋10）×√６÷２
＝27√６＋11√６＝38√６
国私立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
