平均47.2点(前年比;-5.6点)
最高点―98点、最低点―0点
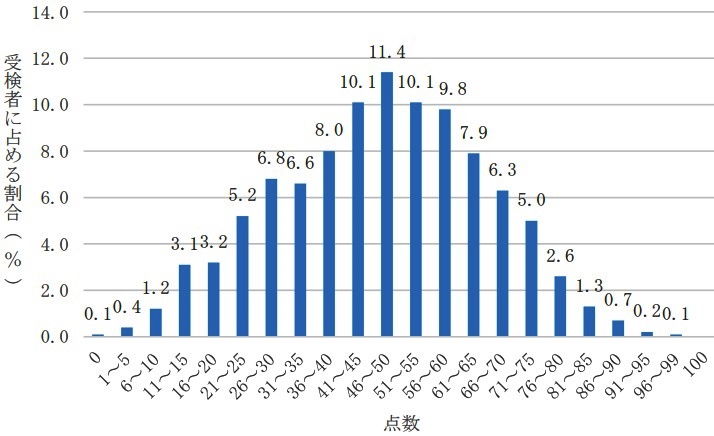
問題はこちら→東進ハイスクールさん(解答)
大問1(計算)
(1) 96.7%
7+(-11)
=7-11
=-4
(2) 74.5%
8/3÷(-6)-1/9
=-4/9-1/9
=-5/9
(3) 94.1%
(-9)2-52
=81-25
=56
(4) 87.2%
3√5+√10÷√2
=3√5+√5
=4√5
(5) 78.9%
-3x2y×4y2÷(-6xy2)
=2xy
(6) 69.4%
(x+y)/4-(x-y)/8
={2(x+y)-(x-y)}/8
(2x+2y-x+y)/8
=(x+3y)/8
大問2(小問集合)
(1) 53.7%
x2+4x-2=0
解の公式を適用して、x=-2±√6
(2) 80.4%
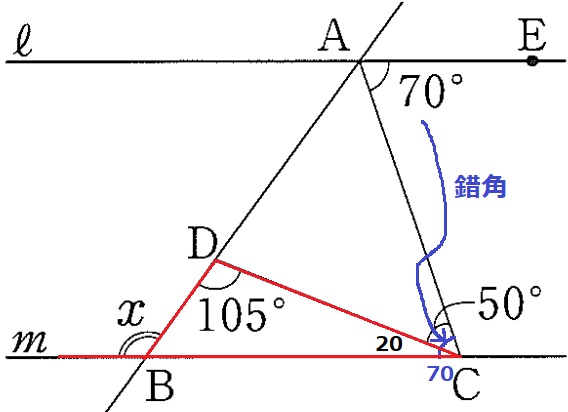
70°を錯角で下ろす。
∠DCB=70-50=20°
△BCDで外角定理→x=105+20=125°
(3) 36.5%
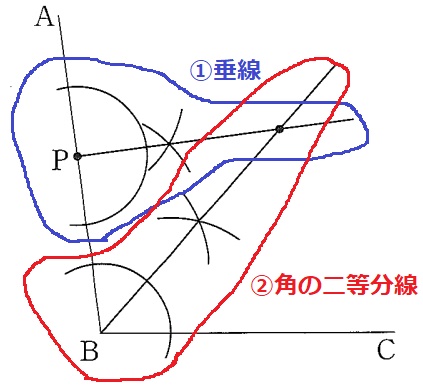
①Pを接点とする→Pを通る垂線
②BA、BCを接線とする→円の中心は2つの半直線から等距離→∠ABCの二等分線
これらの交点が答え。
(4) 27.0%!
比例定数a=-1×(-4)=4
y=4/xが通過する格子点を数える。反比例は双曲線であることに注意。
(1、4)(2、2)(4、1)
(-1、-4)(-2、-2)(-4、-1)
6個
(5) 68.5%
5個から2個を取り出す→5C2=10通り
青は1個しかない。青を含む組み合わせは【青+他4個から1個】→4通り
確率は、4/10=2/5
大問3(数量変化・方程式)
(1)① 57.9%
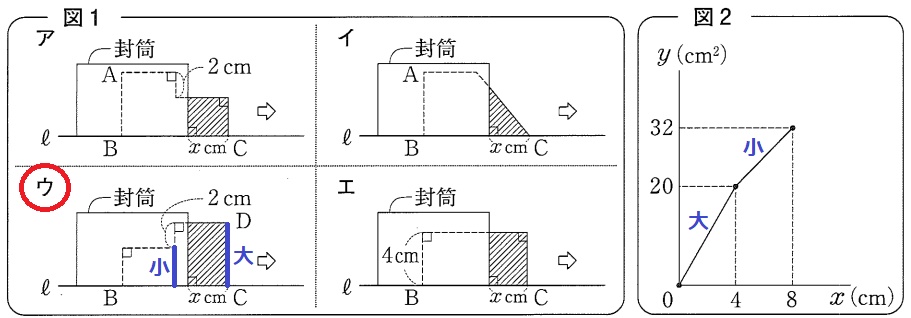
前半の方が後半より傾き(変化の割合)が大きい。
→前半に広い面積が外に出る。
ウ
② 32.0%!
傾き=(yの増加量)÷(xの増加量)=(32-20)÷(8-4)=3
y=3x+bに(x、y)=(4、20)を代入。
20=3×4+b
b=8
y=3x+8
(2)① 81.9%

野菜(にんじん+白菜の合計)がn。
にんじん:白菜=1:7だから、にんじんは1/8n
② 37.7%
答案では表の式をもとに根拠を示して説明する。
塩こうじが27gの場合、野菜の量は、
3/25n=27
n=225
野菜225gに対して塩こうじ27gなので、
野菜240gに対する塩こうじの量は27gでは足りない。
イ
③ 3.6%!!(無答率52.5%)

にんじん:白菜=①:⑩
にんじんを15g足したら①:⑦
白菜が変わっていない点に着目する。
⑩=⑦なので、最小公倍数70で比を統一する。

差の3=15g
野菜の量は80で、この3/25倍が塩こうじにあたるから、
15×80/3×3/25=48g
大問4(データの活用)
(1)① 70.9%
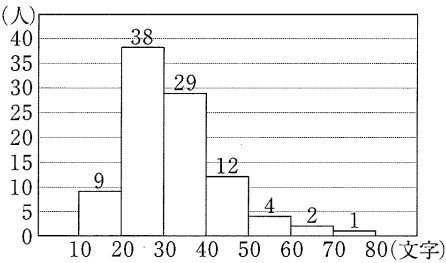
95人の中央値は、(95+1)÷2=48番目の値。
30文字以上40文字未満
② 65.9%
40文字以上の割合を求める。
(12+4+2+1)/95=19/95=1/5=20%
(2)① 57.0%
相対度数…全体に対する度数の割合。
全体の度数が163と122で異なるから、割合である相対度数を用いる。
エ
② 3.6%!!(無答率22.3%)
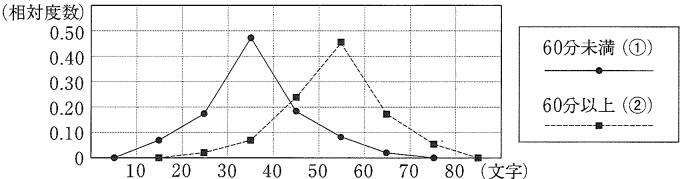
2つの度数分布多角形が同じような形であり、
60分以上のグラフは60分未満のグラフより右側にあるから。
大問5(関数)
(1) 74.5%
y=1/3x2にy=1/3を代入。
1/3=1/3x2
x2=1
Bのx座標はx>0だから、x=1
(2) 59.1%
x=0のとき、最小値y=0
x=-3のとき、最大値y=3
0≦y≦3
(3)① 16.9%!
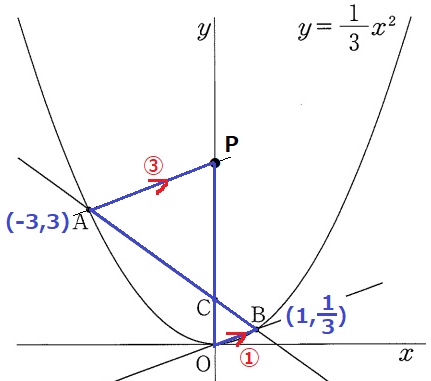
AP//OBより、対頂角と錯角の2角相等で△COB∽△CPA
AとBのx座標から相似比は①:③
面積比は相似比の2乗→△COB:△CPA=1:9
② 0.6%!!!(無答率66.8%)
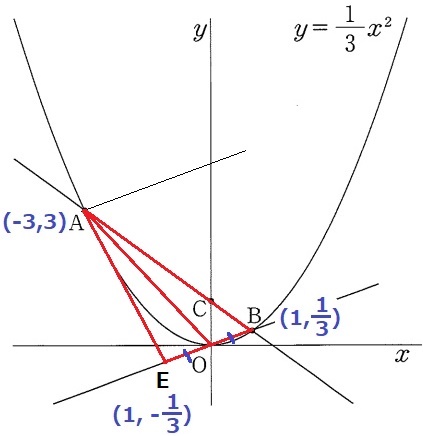
まず、△AOBの2倍にあたる三角形をつくる。
△AOBと△AQBは辺ABで共通→いったん、直線OB上で考える。
BO=OEとなる点Eをとると、高さが2倍になるので△AEB=△AOB×2
Eをx軸上に乗せればいい。

Eを通るABに平行な線をひくと、x軸との交点がQ。
ABの傾きは、(yの増加量)÷(xの増加量)=(1/3-3)÷{1-(-3)}=-2/3
E→Qは左に③、上に②移動するので、1/3×③/②=1/2左にズレる。
Qのx座標は、-1-1/2=-3/2
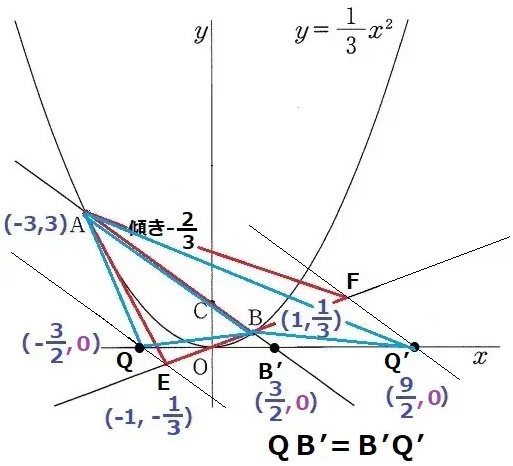
もう1つは、Bを挟んで反対側にEB=BFとなる点Fをとり、Fをx軸に移すとQ’になる。
EとBは原点について対称関係なので、Eと同様にBをx軸のせた点をB’とすると、
E→QとB→B’の移動も対称性があるから、B’(0、3/2)
QB’=B’Q’=3/2-(-3/2)=3
Q’のx座標は、3/2+3=9/2
t=-3/2、9/2
大問6(図形)
(1)① 18.4%!
△ABC≡△EDCの証明。

直径より、AB=ED
弧AC=弧CEより、等しい弧に対する円周角は等しいから、∠ABC=∠EDC
半円の弧に対する円周角より、∠ACB=∠ECD=90°
斜辺と1つの鋭角が等しい直角三角形ゆえ合同。
② 8.9%!!(無答率35.3%)
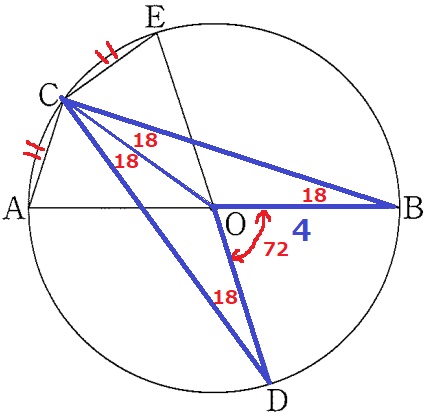
半径は8÷2=4cm
弧EBを求めるには、中心角の∠EOBがわかればいい。
等しい弧から、∠ABC=∠EDC=18°
COに補助線をいれると、半径より△OBCも△OCDも二等辺三角形。
∠OCB=∠OCD=18°
∠BCDは弧BDに対する円周角で、∠BODはその中心角だから(18×2)×2=72°
∠EOB=180-72=108°
弧EBの長さは、4×2×π×108/360=12/5πcm
(2)① 51.9%

正方形ABCDの対角線は各々の中点で交わる→AH=4√2÷2=2√2cm
△OAHは等辺2√2cmの直角二等辺三角形。
辺の比は1:1:√2だから、OA=2√2×√2=4cm
② 11.6%!(無答率38.3%)
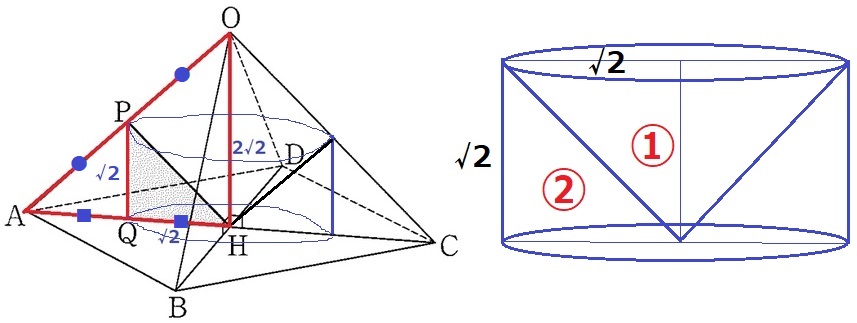
△APQ∽△AOH(中点連結定理)より、PQ=2√2÷2=√2cm
同様に、QH=√2cm
回転体は円柱から円錐をくり抜いた形になる。
円柱の体積を③とすると円錐は①、求積すべき立体の体積は②。
√2×√2×π×√2×②/③=4√2/3πcm3
③ 1.8%!!(無答率69.4%)
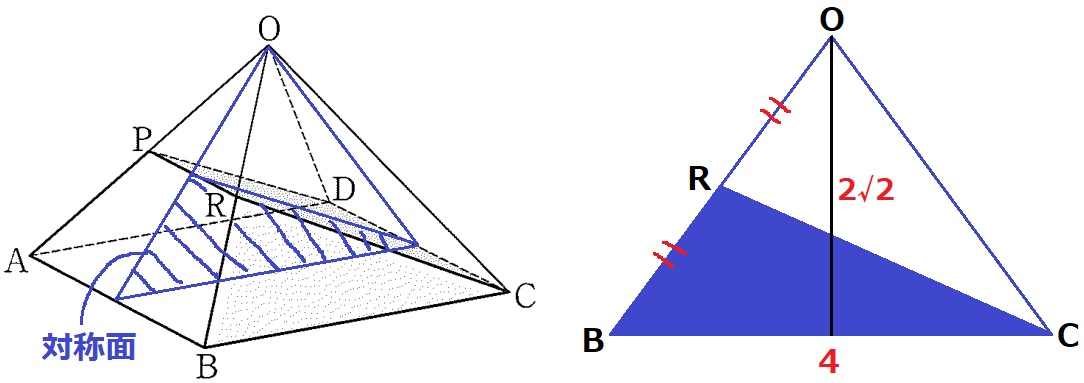
求積すべき立体を左右対称に分ける対称面を底面と見立て、断頭三角柱から体積を求める。
対称面の面積は、△OBC÷2=4×2√2÷2÷2=2√2cm2

高さの平均は(AB+DC+PR)÷3=(4+4+2)/3=10/3cm
よって、2√2×10/3=20√2/3cm3
●講評●
大問1
配点18点。全問正解したい。
大問2
(1)得点源のはずなのに正解者が約半数!
xの係数が偶数なので、b=2b’が使える。
(3)よくある形式の作図。
(4)反比例の格子点の数。中1の範囲だが正答率がよくない。
大問3
(1)①解答に必要なのは、4秒前後の変化の割合。
厚紙の高さ5cmや2cmは不要であった。
②一次関数の基本問題だが、正解者が3人に1人!
(2)③変わらない方の比ですべて統一するとなんとかなる。
求めたいのは塩こうじなので野菜×3/25。野菜の比が80に相当する。
大問4
判断しやすい設問が多い。
全体の度数が異なる場合、度数分布多角形を使って分布の傾向を調べる。
(2)②グラフの形が類似している点にも触れたい。
大問5
(3)②ABが共通辺なので、ABを底辺としたときの高さ2倍が面積2倍。
高さはとりあえずOB上で考える。そのあとでx軸に移してQの位置を定める。
ABの傾きが分数なので処理能力も問われる。
EとBの対称性に気づくと、Bをx軸に移した点を中心として、反対側の等距離にもう1つのQが現れる。
大問6
(1)①直接、∠EOBは出しずらい。
四角形OBCDがブーメラン型であるのを利用して∠BODを求めててもいい。
(2)①OAを斜辺とする直角三角形はどこか。
②中点連結定理で√2cmを出す。体積は柱の2/3倍で求められる。
③テクニックを身につけていれば解きやすい。
断頭三角柱は大阪C問題ではお馴染みだが、昨年の山梨でも出題されている。


コメント