2020年度　早稲田実業高等部過去問【数学】大問３解説

問題ＰＤＦ
（１）
ｘ、ｙについての連立方程式
ｙ＝ａｘ＋２
ｙ＝ｂｘ－３
が解をもたないための条件を、定数ａ、ｂを用いて表せ。

（２）
Ａ、Ｂ、Ｃ、Ｄ、Ｅを定数とする。
ｘ、ｙについての４つの方程式
Ａｘ＋Ｂｙ＝－12　…（ア）
Ｂｘ－Ａｙ＝16　…（イ）
６ｘ－８ｙ＝Ｃ　…（ウ）
Ｄｘ－６ｙ＝Ｅ　…（エ）
は、以下の条件をすべて満たすとする。
条件Ⅰ：（ア）と（ウ）を連立方程式として解いても、解はない。
条件Ⅱ：（ア）と（エ）を連立方程式として解くと、解はｘ＝８、ｙ＝９である。
条件Ⅲ：（ウ）と（エ）を連立方程式として解いた解は、
（ア）と（イ）を連立方程式として解いた解より、ｘの値は６大きく、ｙの値は２大きい。
このとき、次の①、②に答えよ。
①Ａ、Ｂの値をそれぞれ求めよ。
②Ｃ、Ｅの値をそれぞれ求めよ。

＠解説＠
（１）
２つの式が解を持たない場合とはどういうときか。

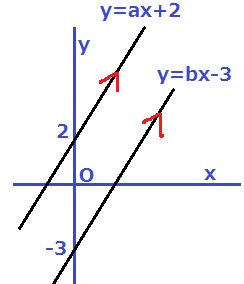
グラフに置き換えてみよう。
２つの式が解を持つとき、グラフ上では直線の交点が解となる。
解がないということは交わらない。すなわち、２本のグラフは平行。
→傾きであるａとｂが等しい。
ａ＝ｂ

＠留意点＠

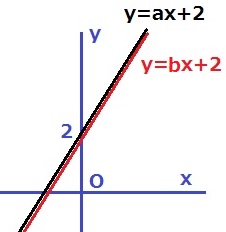
傾きが同じでも、切片が等しければ２本の直線が重なってしまう。
ｘにどんな値をいれても式が成立することになる。
解が無数にある方程式を不定といい、解なしの方程式を不能という。

（２）①
Ａｘ＋Ｂｙ＝－12　…（ア）
６ｘ－８ｙ＝Ｃ　…（ウ）
これらを連立で解くと解がない。

（ア）をｙについて解くと、
ｙ＝－Ａ/Ｂｘ－12/Ｂ
（ウ）をｙについて解くと、
ｙ＝３/４ｘ－Ｃ/８

解がない→傾きが等しいから、－Ａ/Ｂ＝３/４→Ａ/Ｂ＝－３/４
ＡとＢは約分されて－３/４になるかもしれないので、比例定数ｋ（ｋ＞０）を用いて、
（Ａ、Ｂ）＝（－３ｋ、４ｋ）もしくは（３ｋ、－４ｋ）

ここで条件Ⅱより、（ア）はｘ＝８、ｙ＝９の解を持つときがある。
８Ａ＋９Ｂ＝－12
これに（Ａ、Ｂ）＝（－３ｋ、４ｋ）を代入すると、
－24ｋ＋36ｋ＝12ｋ＝－12となり、ｋが負の数で不適。

（Ａ、Ｂ）＝（３ｋ、－４ｋ）を代入。
８Ａ＋９Ｂ＝24ｋ－36ｋ＝－12ｋ＝－12
ｋ＝１
Ａ＝３ｋ＝３
Ｂ＝－４ｋ＝－４
Ａ＝３、Ｂ＝－４

②
（ア）（イ）に前問のＡ＝３、Ｂ＝－４を代入。
３ｘ－４ｙ＝－12
－４ｘ－３ｙ＝16
これを解くと、ｘ＝－４、ｙ＝０

条件Ⅲより、（ウ）（エ）で解いた解は、
ｘ＝－４＋６＝２、ｙ＝０＋２＝２

（ウ）に放り込む。
Ｃ＝６×２－８×２＝－４

今度は、（エ）に放り込む。
２Ｄ－12＝Ｅ…①
条件Ⅱより、（エ）にｘ＝８、ｙ＝９を放り込む。
８Ｄ－54＝Ｅ…②

①、②から、２Ｄ－12＝８Ｄ－54
Ｄ＝７
最後に①に代入。
Ｅ＝２×７－12＝２
Ｃ＝－４、Ｅ＝２
国私立高校入試解説ページに戻る