2021年度　豊島岡女子学園高校過去問【数学】大問２解説

問題ＰＤＦ
（１）
ｘについての２次方程式
ｘ²＋（２ａ²－ａ－１）ｘ－４ａ－９＝０がｘ＝３を解にもつとき、
定数ａの値をすべて求めなさい。

（２）
１次関数ｙ＝ａｘ＋１について、ｘの変域が－１≦ｘ≦２のとき、ｙの変域はａ≦ｙ≦ｂです。
このとき、定数ａの値をすべて求めなさい。

（３）
ａ、ｂ、ｃは、１＜ｃ＜ｂ＜ａ＜20を満たす整数とします。
170ａ＋169ｂ＋168ｃの値が13の倍数となるとき、
考えられるａ、ｂ、ｃの組は全部で何組ありますか。

（４）

上の図のように、円と半円があり、
円は半円の弧ＡＢと直径ＡＢにそれぞれ点Ｐと点Ｑで接しています。
半円の中心をＯとし、∠ＰＢＱ＝58°であるとき、∠ＯＰＱの大きさを求めなさい。

（２）
ｙの最小値ａのｘ座標が〔－１or２〕は、傾きａが〔正or負〕による。
傾きａの正負で場合分け。
◆ａ＞０のとき
直線は右上に傾く。ｘ＝－１のとき、ｙ＝ａ
（－１、ａ）をｙ＝ａｘ＋１に代入。
ａ＝－ａ＋１
ａ＝１/２
これはａ＞０を満たす（この条件はきちんと確認する）。

◆ａ＜０のとき
直線は右下。ｘ＝２のとき、ｙ＝ａ
（２、ａ）をｙ＝ａｘ＋１に代入。
ａ＝２ａ＋１
ａ＝－１
これはａ＜０を満たす。
よって、ａ＝－１、１/２

（３）
169は13の平方数。
この手のタイプは真ん中の数で揃えると上手くいく場合がある。

170ａ＋169ｂ＋168ｃ
＝（169＋１）ａ＋169ｂ＋（169－１）ｃ
＝169（ａ＋ｂ＋ｃ）＋ａ－ｃ

最後のａ－ｃが13の倍数であれば、全体が13の倍数となる。
１＜ｃ＜ａ＜20の範囲で、ａ－ｃの差が13の倍数となるのは13のみ。
（ａ、ｃ）＝（19、６）（18、５）（17、４）（16、３）（15、２）
５通り

ｃ＜ｂ＜ａ→ｂはａとｃのあいだの数。
ａとｃの差は13で一定だから、ｂは12通りずつある。
*（ａ、ｃ）＝（19、６）であれば、ｂは７～18の12個。
12×５＝60組

（４）

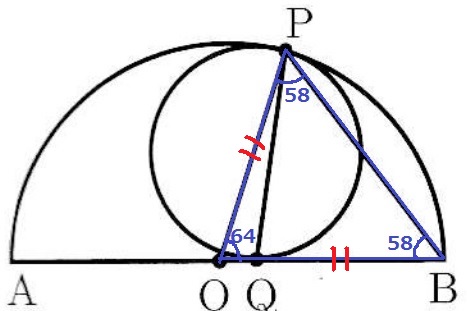
半径ＯＰ＝ＯＢより、△ＯＰＢは二等辺。
∠ＰＯＢ＝180－58×２＝64°

ここで接点Ｐ、Ｑを用いる。
接線と半径は接点で垂直に交わる。
Ｐは円と半円の接点なので、半円の半径ＯＰも接線に対して垂直である。
→円の直径はＯＰ上にある。
Ｑから接線ＯＢに対して垂直な線をひき、ＯＰとの交点をＯ’とすると、
Ｏ’はＯ’Ｐ、Ｏ’Ｑを半径とする円の中心である。

△ＯＯ’Ｑの内角から、∠ＯＯ’Ｑ＝180－（64＋90）＝26°
∠ＯＰＱは26°を中心角とする弧に対する円周角であるから、
∠ＯＰＱ＝26÷２＝13°
国私立高校入試解説ページに戻る