問題PDF
1辺の長さがaである5つの立方体をすきまなく重ねて下の図のような立体を作る。立方体ABCD-EFGHは、線分EGが線分IK上にあり、線分EGの中点と線分IKの中点が一致する位置にある。この立体を3点D、M、Oを通る平面で切り、2つに分ける。このとき、次の各問いに答えなさい。

(1)
切り口の面積を求めなさい。
(2)
2つに分けた立体のうち、体積の大きい方の立体の体積を求めなさい。
@解説@
(1)
まずは断面図を作成する。

うえの立方体が奥ではなく、半歩手前にズレているのが厄介。
断面図は平行関係を意識しよう。ポイントはMO//QR
もう1つはDとQRの中点、MOの中点は1直線上に並び、距離が1:1であること。

分割すると合同な二等辺三角形が8つできる。
二等辺の底辺は、1辺が1/2aである正方形の対角線で√2/2a
高さは二等辺の底辺の半分である√2/4aと立方体の1辺aで三平方→3√2/4a
(上図の緑の直角三角形)
断面積は、√2/2a×3√2/4a÷2×8=3a2
(2)

MOから出発すると切り口は後ろに向かっていくから、体積が大きいのはNを含む手前の立体。
うしろの立体が錐の計算をしやすいので、後ろを求めて全体から引く。
赤い三角錐の体積は、1/2a×1/2a÷2×a÷3=1/24a3
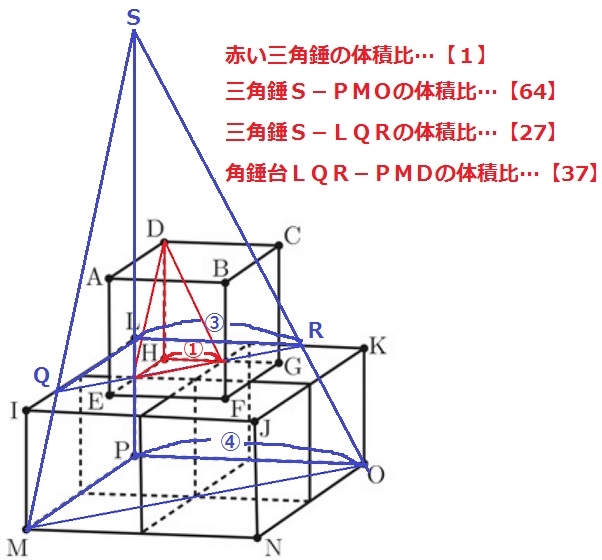
MQ、PL、ORを延長した交点をSとする。
赤い三角錐の底辺の1辺を①とすると、PO=④、LR=③
体積比は相似比の3乗。
赤い三角錐の体積を【1】とすると、三角錐S-PMOは④3=【64】
三角錐S-LQRは③3=【27】、角錐台LQR-PMDは【64】-【27】=【37】
小さいほうの立体の体積は、赤い三角錐+角錐台=1/24a3+1/24a3×37=38/24a3=19/12a3
5つの立方体の体積は5a3
大きいほうの立体の体積は、5a3-19/12a3=41/12a3



コメント