問題PDF
4桁の正の整数Mがあり、Mの千の位の数と百の位の数をそれぞれ十の位の数と一の位の数とする2桁の正の整数をAとし、Mの十の位の数と一の位の数をそれぞれ十の位の数と一の位の数とする2桁以下の整数をBとする。例えば、M=2023のときA=20、B=23であり、M=2003のときA=20、B=3である。MがAとBの積ABの倍数であるとき、すなわち、Mが整数mを用いてM=mABと表されているとき、次の問いに答えよ。
(1)
BがAの倍数であることを文字式を用いて説明せよ。
(2)
(1)から、Bを整数nを用いてB=nAと表したとき、
nが100の約数であることを文字式を用いて説明せよ。
(3)
A、Bの値の組(A、B)をすべて求めよ。
@解説@
(1)
『BがAの倍数である』→B=A( )の形にもっていく。
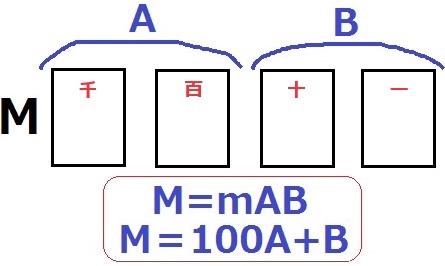
AとBの関係式をつくる。
仮定より、M=mAB …①
MをAとBを使って別の方法で表す。
Aが百の位以上であることに注目して、M=100A+B …②
①、②より、100A+B=mAB
B=mAB-100A
=A(mB-100)
mとBは整数→mB-100は整数なので、BはAの倍数である。
(2)
『nが100の約数である』→n( )=100の形に持っていく。
(*nをカッコ内の数字でかけると100→100はnで割り切れる)
前問で導いた式にB=nAを代入すると、
nA=A(mnA-100)
両辺をAで割る。
文字で割る場合、0で割れない点に配慮すること!
Aは2桁の正の整数でA≠0だから、Aで割ることが許される。
n=mnA-100
mnA-n=100
n(mA-1)=100
mとAは整数→mA-1は整数だから、nは100の約数である。
(3)
前問の答えを活用する。
100の約数→1、2、4、5、10、20、25、50、100
n(mA-1)=100からmA-1も100の約数なので、
mA=2、3、5、6、11、21、26、51、101
Aは正の2桁の整数→mAの値は1桁ではない→2、3、5、6は×。
101は素数で1×101しかないから×!
mA=11、21、26、51
(m×A)=(1×11)(1×21)(1×26)(2×13)(1×51)(3×17)
(1)のB=A(mB-100)に代入して、(A、B)の組み合わせを絞る。
MはAとBの数を並べた4桁の正の整数だから、AとBはともに正の整数である。
もし、m=1のとき、B=A(B-100)
Bは2桁以下の整数なのでカッコ内は負、Aは正→B=正×負=負となって不適。
m≠1
(m、A)=(2、13)(3、17)しかない。
●(m、A)=(2、13)
B=13(2B-100)
B=52
●(m、A)=(3、17)
B=17(3B-100)
B=34
(A、B)=(17、34)(13、52)
@@@

中学では算数バージョンで出題されています。


コメント