2021年度　渋谷教育学園幕張中学過去問【理科】大問４解説

問題ＰＤＦ
てつお君は趣味で、電車の乗り換え案内を作成しました。
さらに興味を持ったてつお君は、駅間の距離も調べることにしました。
次の文章は、てつお君が先生に相談したときの会話です。

てつお：先生！駅間の距離を調べる良い方法はありませんか。
先生：時間と速さの関係のグラフから距離を求めることができるよ。
てつお：どうしてですか？！
先生：例えば、一定の速さ10ｋｍ/時（時速10ｋｍを10ｋｍ/時と書き表します）で
　５時間進んだら、どれだけの距離を移動したことになるかな。
てつお：_①　　　　ｋｍです。
先生：どうやって求めたのかな。
てつお：「_（あ）　　　×_（い）　　　＝距離」の式を用いて計算しました。
先生：そうだよね。では、横軸を時間、縦軸を速さにしてグラフを書いてみよう。
てつお：図１のようになりました。

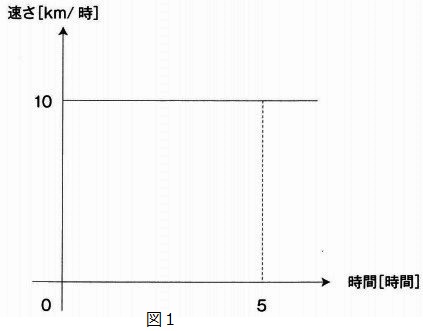
先生：では、時間と速さのグラフをよく観察してごらん。
　距離を求めた計算式は、グラフの何を計算することになるかな。
てつお：図２の塗りつぶした部分の_（う）　　　です。
先生：正解！！

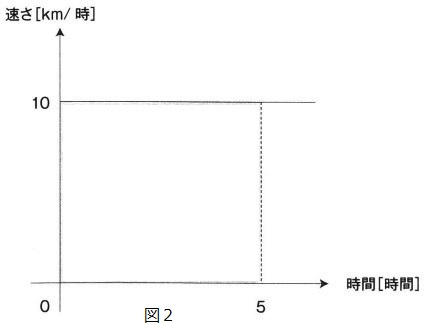
先生：では、図３のように速さが変化するグラフの場合は、
　グラフのどの部分が５時間で移動した距離を示すかな。

てつお：うーん、分かりません…。
先生：では、図４のように、グラフを短い時間間隔に分け、長方形を使って考えてみよう。

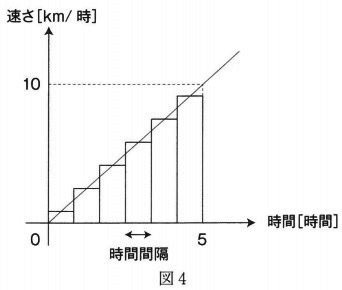
先生：図４の時間間隔をさらに短くしていくと、図５のように、
　たくさんの長方形で埋め尽くすことになるよね。

てつお：はい。
先生：では、１つ１つの長方形の_（う）　　　　は何を表しているのかな。
てつお：短い時間の間に移動した距離です。
先生：正解。よって、５時間の間に移動した距離は、
　それぞれの細長い長方形の_（う）　　　　を足し合わせたものとして考えることができるよ。
　図５のグラフの時間間隔をさらに短くしていくと、５時間の間に移動した距離は
　図のどの部分になるのかな。
てつお：移動した距離は、図のこの部分ですね。
（てつおくんはそう言いながら、図３の一部分を塗りつぶしました）
先生：その通り！では、図３のように速さが変化した場合、
　５時間の間に移動した距離はいくらかな。
てつお：_②　　　　ｋｍです。
先生：大正解！！
てつお：先生、ありがとうございました！

（１）
会話文の①、②には適切な数値を答え、（あ）～（う）には適切な語句を答えなさい。

てつお君は先生との会話のあと、図６の幕張駅から幕張本郷駅までの距離を求めるために、
幕張駅から乗車し、幕張本郷駅に向かいました。

電車の先頭車両の速度計を利用して、10秒おきの速さを調べました。
速度計の値は、その時間の瞬間の速さを示します。結果は表１のようになりました。
電車が発車してから60秒後までは、一定の割合で速さが増していきます。
60秒後から120秒後までは一定の速さで進みます。
120秒後から一定の速さで減っていき、150秒後に停車しました。
ただし、電車と駅の長さは考えないものとします。

（２）
表１の値を点（●）ではっきりと示し、時間と速さのグラフを書きなさい。

（３）
72ｋｍ/時は何ｍ/秒ですか。

（４）
幕張駅から幕張本郷駅までの距離は何ｍですか。

次に、てつお君は幕張本郷駅から乗車し、幕張駅に戻りました。
てつお君は同じように、10秒おきの速さを調べました。
時間と速さの関係のグラフは図７のようになりました。

２本の電車が幕張駅と幕張本郷駅を同時に発車してすれ違う場合、
次の問いに答えなさい。

（５）
出発してから２本の電車がすれ違うまでの時間は何秒ですか。
小数第１位まで答えなさい。

（６）
電車がすれ違う位置と幕張駅との間の距離は何ｍですか。整数で答えなさい。

＠解説＠
（１）①50②25（あ）速さ（い）時間（う）面積
基本。
①10ｋｍ/時×５時間＝50ｋｍ
（あ）（い）…速さ×時間＝距離

（う）…縦軸が速さ、横軸が

（２）下図参照。

機械的にプロットして線をひく。
きれいな形になる。０にも●を忘れないように(ﾉ)`ω´(ヾ)

（３）20ｍ/秒
簡単すぎる(;^ω^)
時速ｋｍから秒速ｍは×10/36倍。
72×10/36＝20ｍ/秒

（４）2100ｍ

速さ―時間のグラフでは、距離が面積であらわされる。
さきほどの台形の面積を求める
高さは72ｋｍ/時ではなく、20ｍ/秒で計算。
（60＋150）×20÷２＝2100ｍ

（５）77.5秒

ありがたいことに最高速度20ｍ/秒は同じ。
最初の加速シーンが面倒なので、いったん60秒後にそれぞれが走った距離を求める。
幕張発が600ｍ。幕張本郷発が800ｍ。
残りは2100－（600＋800）＝700ｍで、両者は１秒あたり40ｍ近づく。
700÷40＝17.5秒
したがって、60＋17.5＝77.5秒

（６）950ｍ

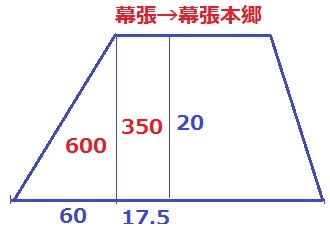
60秒から17.5秒を追加。
600＋20×17.5
＝600＋350＝950ｍ

＠ｖ－ｔグラフ＠
縦軸に速度ｖ（velocity）、横軸に時間ｔ（time）をとるグラフをｖ－ｔグラフという。

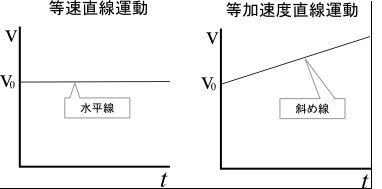
物理解体新書より。
速度と方向が一定である等速直線運動をｖ－ｔグラフであらわすと水平線、
これに一定の速度の変化がつく等加速度直線運動では斜め線になる。
Ｖ₀はｔ＝０のときの速さＶ（初速度）である。

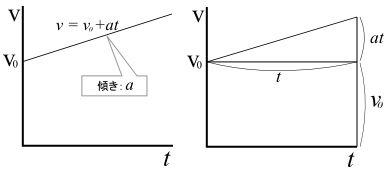
加速度ａは傾きで示される。傾きが大きいと加速度も大きい。
（加速度ａ＝速度ｖ/時間ｔ→ｖ＝ａｔ）
減速は斜め左下となり、傾きは負（マイナス）になる。
初速度のある等加速度直線運動の距離は長方形と三角形の面積の和であり、
文字式であらわすと、ｖ₀ｔ＋１/２ａｔ²となる。
くわしくは高校物理で習います。
難関中学（理科）解説ページに戻る