2019年度　ラ・サール中学過去問【理科】大問４解説

問題ＰＤＦ
〔Ａ〕
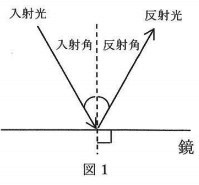
鏡に向かって進む光を入射光、鏡ではね返った光を反射光といい、
入射光と面に垂直に立てた直線とのなす角を入射角、
反射光と面に垂直に立てた直線とのなす角を反射角といいます。
図１のように、光は平らな鏡で反射すると
入射角と反射角が等しくなるという性質を持っています。

この性質を用いて、以下の問いに答えなさい。

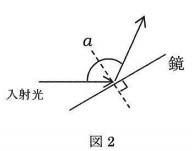
（１）図２のように水平な面から30度傾けた鏡に、
水平な面と平行に光をあてました。
このときの入射角と反射角の和となす角ａは何度ですか。

（２）図２の状態からさらに鏡を10度傾け、
水平な面と鏡のなす角度が40度となるようにした後、
水平な面と平行に光をあてました。
このときの入射角と反射角の和は、（１）の角ａから何度だけ減少しますか。

次に、図３のように鏡Ａを水平に、
鏡Ｂを鏡Ａに対して垂直においたところに光をあてることを考えます。
水平な面と30度の角をなす光を鏡Ａにあて、さらに鏡Ｂで反射させました。

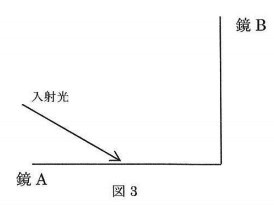
（３）鏡Ｂで反射した光は水平な面と何度の角をなしますか。
ただし、答えは０度から90度の間で答えなさい。

（４）鏡Ａを固定し、鏡Ｂを鏡Ａ側に倒していったところ、
鏡Ｂで反射した光が水平になりました。
このとき鏡Ｂを図３の位置から何度倒しましたか。

（５）（４）よりもさらに鏡Ｂを鏡Ａ側に倒していったところ、
鏡Ｂで反射した光が水平な面と垂直になりました。
このとき鏡Ｂを図３の位置から何度倒しましたか。

〔Ｂ〕
材質が均一な板を水平に支えるには、板の真ん中を支えればよいです。
このように、もののバランスを保つことができる位置を「重心」といいます。
また、「重心」とはものが地球から真下に引っ張られる力（重力）がはたらく代表点、
すなわち、ものの重さがかかる点と考えることができます。
いま、材質が均一な一枚の薄い板を用意し、図１のように、厚さ、幅は同じで
長さの異なる３枚を分け、それぞれＡ、Ｂ、Ｃとします。

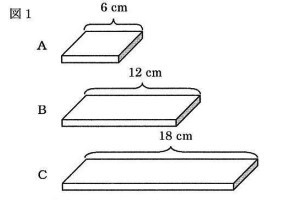
これらの板を幅がそろうように重ね、図２のように水平な台の上にまっすぐに置き、
重ねる枚数や順序、板を置く位置をいろいろと変え、
板全体のバランスをとる〔実験１〕～〔実験３〕をしました。

〔実験１〕
Ｃの上にＡまたはＢを重ね、それぞれの先端をできるだけ右側に出すようにしたところ、
Ａはその先端がＣの右端から３ｃｍを超えたときに（図３）、
Ｂはその先端がＣの右端から６ｃｍを超えたときに（図４）傾いて落ちてしまいました。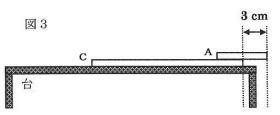 

〔実験２〕
Ｃの上にＡ、Ｂを２枚とも重ね、一番上のＡの先端をＣの右端からできるだけ右側に出すようにしたところ、Ａの先端がＢの右端から３ｃｍを超えたときに（図５）傾いて落ちてしまいました。

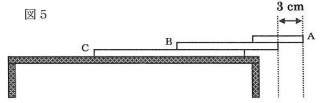
（１）〔実験２〕について述べた次の文中の空欄に適当なものを選びなさい。
まず、Ｂに対して、Ａが傾いて落ちない状況について考えてみます。
Ａの重心がＢの右端（これ以降、Ｘと呼ぶことにします）より右側にあるように置いたときは、Ａはその重力によって、Ｘに対し{①ア、時計回り　イ、反時計回り}に傾いて落ちようとしますが、逆に左側にあるように置いたときは、それとは逆の効果があらわれます。したがって、Ａの重心とＸとがちょうど一致するように置いたときが、Ａのバランスを保つことができる限界であることがわかります。なお、ＸにはＡの板の重さがかかっていることになります。
さらにこの状態のまま、Ｃに対して、ＡとＢが傾いて落ちない状況について考えてみます。
この場合も、ＡとＢを合わせた板の重心とＣの右端（これ以降、Ｙと呼ぶことにします）とがちょうど一致するように置いたときが全体のバランスを保つことができる限界となります。なお、このときＹにはＡとＢを合わせた板の重さがかかっていることになります。また、てこの原理により〔Ａの重心とＹとの距離〕と〔Ｂの重心とＹとの距離〕との比は、
{②ア、1：1　イ、1：2　ウ、1：3　エ、2：1　オ、3：1　カ、2：3　キ、3：2}
の関係になってします。
以上のことより、Ａの先端はＹから最大{③ア、5　イ、6　ウ、7　エ、8　オ、9}ｃｍだけ右側に出すことができたとわかります。

（２）図６のように、〔実験２〕と板を重ねる順序は変えずに真ん中にあるＢの先端をＣの右端からできるだけ右側にだすようにした場合について考えて見ます。

このとき、Ｂの先端は、Ｃの右端から最大何ｃｍだけ右側に出すことができますか。

〔実験３〕
Ａ～Ｃの３枚の板を、一番下の板が台の右端から出るように重ね、どれかの板の先端を台の右端からできるだけ右側に出すようにしたところ、その板の先端が台の右端からａｃｍを超えたときに傾いて落ちてしまいました。

（３）〔実験３〕において、図７のような順序で板を重ね、一番下のＡの重心が台の右端よりも右側にくるようにした状態で、一番上のＣの先端をできるだけ右側に出すようにした場合について考えてみます。

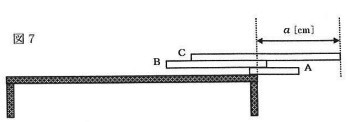
このとき、Ｃの先端を台の右端から右側に出すことができる最大の距離であるａは
何ｃｍになりますか。

（４）〔実験３〕において、一番下をＡの板にし、Ａの重心が台の右端よりも左側にくるようにした状態で行いました。板を重ねる順序や、板を置く位置を変えるなかで、ａｃｍを最も大きくできた場合について、以下の①～③に答えなさい。
①一番上の板はＢ、Ｃのうちどちらですか。
②台の右端から先端を最も右側に出すことができる板はＡ～ｃのうちどれですか。
③ａは何ｃｍになりますか。

〔Ａ〕（１）120度

「水平な面」は真横。
入射光は水平な面と平行にあてたので、
入射光と鏡のなす角が30度。
ａ＝180－30×２＝120度

（２）20度
前問の30を40にする。
180－40×2＝100度
よって、120－100＝20度分だけ減少した。
鏡を傾けた角の２倍の角でちぢまる。

（３）30度
図３で光の経路を書いてみる。

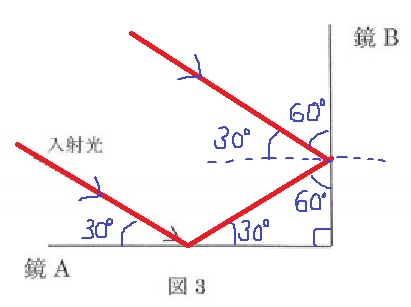
求めるのは鏡Ｂではなく、水平な面に対しての角度！
６０度では×。
入射光と平行になり、答えは30度。

（４）15度
作図問題。
入射光と水平な光を先に書く。

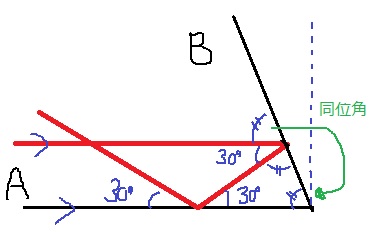
30度を錯角で上にあげる。
（180－30）÷２＝75度
上の75度を同位角で下にさげる。
鏡Ｂを傾けた角度は、90－75＝15度

（５）60度
作図問題２。
これも入射光と最後の反射角を先に書いて作図する。

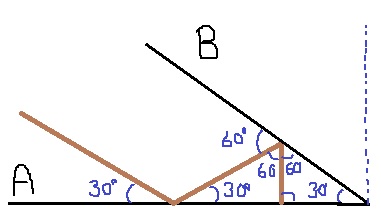
入射光と鏡Ｂは平行になる。
傾けた角度が、90－30＝60度

〔Ｂ〕（１）①ア　②エ　③ウ
重心は各板の真ん中。重心までは板をズラすことができる。

①Ａの重心はＢの右端（Ｘ）までズラせる。
Ｘを超えて右に行ってしまうと、重力でＡは落ちてしまう。
落ちるときの様子を思い浮かべると、Ａは時計回りに傾く→ア。
②後の問題でも計算するので、ここで確実に理解しておきたい。

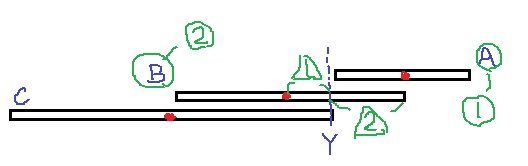
赤丸●が重心。ＡとＢを合わせた重心がＹにくればいい。
ＡとＢの重さが１：２なので、支点（Ｙ）からの距離は２：１→エ。
③Ｙ～Ａ間は、６×２/３＋３＝７ｃｍ→ウ。

（２）８ｃｍ
今度は最上段のＡを左に移動させ、Ｂの右端を台からなるべく離す。
Ｂが右に落ちないようにするには、Ａをなるべく左側に寄せて重しにする。
（重しになれば、Ｂは時計回りの方向で落ちない）

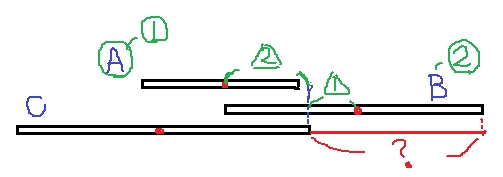
Ａの重心はＢの左端に乗せる。求める場所は赤線。
６×１/３＋６＝８ｃｍ
作図がきちんとできれば立式は容易だが、作図ができないと落とす。

（３）10.9ｃｍ
Ｃの右端をできるだけ台から遠ざける。
上からトップダウンで考える。
Ｃを右にズラしたいので、Ｃの重心はＢの右端に置く。
Ｂを左に置き、土台となるＡは右側に設置する。
Ｂ＋Ｃを１つの物体として捉え、（Ｂ＋Ｃ）を少しでも右に寄せるため。
（Ｂ＋Ｃ）の重心をＡの左端にセッティング。
重さの比は、Ｂ＋Ｃ：Ａ＝５：１だから、
支点からの距離は逆比で１：５。
求めたい長さは、台～Ｃの右端。
【②＋９－△１】を計算すればいい。
６×２/５＋９－３×１/６＝10.9ｃｍ
作図が大変・・・(;￣Д￣)

（４）①Ｂ　②Ｃ　③13.1ｃｍ
最も短いＡを土台にしたとき、どのような積み方をすれば板の橋が台から離れるか？
ポイントを稼げるのはＣ。
なぜなら、全長が最も長いので、重心（真ん中）～端までの長さも最も長く、
一層せり立たせることができるから。
Ｃを右にズラすには、Ｂが左側で重しの役割をしておく。

↑ここまで作図するのに一苦労。
求める場所は、台～Ｃの右端なので、【△１＋②＋９】。
３×１/６＋９×２/３＋９＝13.1ｃｍ
サクズ(乂’ω’)・・・イノチ!!! └(‘ω’)┘
難関中学（理科）解説ページに戻る