問題PDF
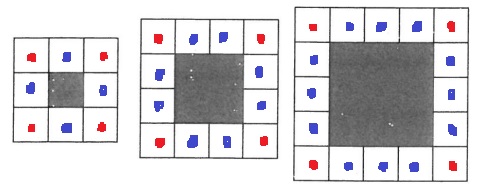
黒い正方形のまわりに1辺の長さが1cmの正方形を並べます。下の図は、左から1辺の長さが1cm、2cm、3cm…の黒い正方形のまわりに白い正方形を並べたものです。

白い正方形のマスの中に、1は1個、2は2個、3は3個…のように整数AはA個使い、ある整数から連続した2種類以上の整数を並べます。たとえば、図1の左のように、黒い正方形の1辺の長さが2cmのとき、3を3個、4を4個、5を5個使うと、ちょうど並べきることができます。しかし、図1の右側のように、4を4個、5を5個、6を6個ではちょうど並べきることができません。また、図2のように、黒い正方形の1辺の長さが8cmのときは、1から8までと、11から13までの整数をちょうど並べきることができます。

このとき、次の各問いに答えなさい。
ただし、(2)、(3)では考えられるものを「〇~〇」のように書きなさい。たとえば、図1の左側の場合は「3~5」、図2の場合は「1~8と11~13」と表すことにします。
(1)
黒い正方形の1辺の長さにかかわらず、連続した2種類の整数だけでは白い正方形のマスの中に整数をちょうど並べきることができません。その理由を説明しなさい。
(2)
黒い正方形の1辺の長さが9cmのとき、白い正方形のマスの中に整数をちょうど並べきるには、いくつからいくつまでの整数を並べればよいですか。考えられるものをすべて答えなさい。
(3)
黒い正方形の1辺の長さが14cmのとき、白い正方形のマスの中に整数をちょうど並べきるには、いくつからいくつまでの整数を並べればよいですか。考えられるものをすべて答えなさい。
(4)
黒い正方形の1辺の長さが100cmまでの中で、白い正方形のマスの中に整数をちょうど並べきることができないのは、黒い正方形の1辺の長さが何cmのときですか。考えられるものをすべて答えなさい。
@解説@
(1)
海陽学園にありそうな説明問題。
黒い辺の長さから白い正方形の数を求める。
●…(黒い正方形の1辺の長さ)×4、●…4つ角
白い正方形の数(●+●)は4の倍数+4、すなわち、4の倍数(偶数)になる。
一方、連続した2種類の整数の和が奇数。
偶数のマスの中に奇数個の整数は並べきれない。
(2)
黒い正方形の1辺の長さが9cmの場合、白い正方形の数は9×4+4=40個
次におさえておきたいのは、連続する整数の和の関係。
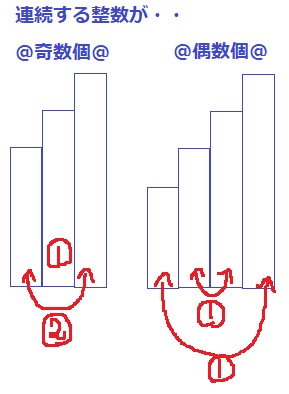
奇数個の場合、真ん中の数を①をおくと、両サイドのペアの和は②になる。
(7・8・9であれば、真ん中の8を2倍した16が両サイドの和)
偶数個の場合、ペアで同じ和が作られる。
(2・3・4・5であれば、3+4=2+5といった具合)
連続する整数が2個の場合は、前問の通り無い。
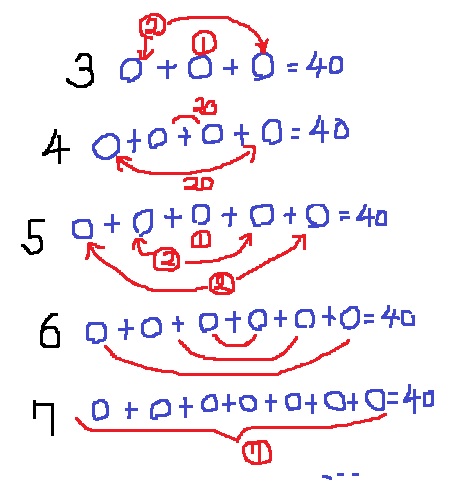
3個の場合は和が③になり、40で割れない。
4個の場合は20+20になるが、連続する2つの整数は奇数なので真ん中のペアが不成立。
5個の場合、⑤=40となり、真ん中の数が8。
8を真ん中にして、(6~10)が見つかる。
6個の場合、ペアが3つできるが40÷3は整数値にならない。
7個は⑦=40で割れない。
8個はペアの和が40÷4=10で、奇数でないと真ん中のペアが不成立。
9個は⑨=40で×。よって、(6~10)しかない。
(3)
黒い正方形の1辺が14cmのとき、白い正方形の数は、14×4+4=60個
前問のように3~14まで数えてもいいが、時間がかかるので少し方法を変えてみる。
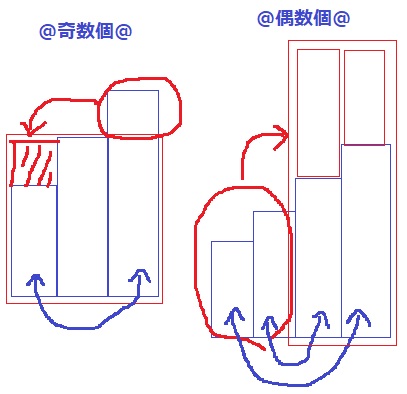
連続する整数が奇数個であっても偶数個であっても、
60を割って商が整数になれば、四角形に均すことができる。
四角形の面積→縦×横
また、連続する整数が偶数個の四角形の縦の長さは必ず奇数になる。
なぜなら、中央のペア2つは連続する2つの整数であり、
その和は奇数なので、他のペアの和(四角形の縦の長さ)も奇数になるから。
つまり、偶数×偶数は自ずと弾かれる。
以上をふまえて、〇×〇=60の組み合わせを調べる。
60×1→整数は2種類以上×
30×2→偶数×偶数ゆえ×
縦20×横3→20が横3つ。すなわち、20を真ん中にして3つ→(19~21)
縦15×横4→ペアの和が60÷4=15
連続する整数が偶数個のとき、中央に近いペアは連続するので差が1。
和が15で差が1→(7・8)のペアを真ん中にして連続する8つの数字→(4~11)
縦12×横5→真ん中を12にして前後の4つを含む→(10~14)
10×6→偶数×偶数ゆえ×
よって、(4~11)(10~14)(19~21)
*もちろん、上記の方法で(2)も素早く解ける。
甲陽学園でも似たようなものが出題されました。

(4)
『偶数×偶数は弾かれる』←これを使う。
偶数×偶数の積→2の素因数だけで構成される数→2のベキ乗!
つまり、白い正方形のマスが2のベキ乗個だと、
連続する整数をいかに組み合わせても2のベキ乗にならず、整数がマスからあぶれてしまう。
(1)より、(黒い正方形の1辺)×4+4=白い正方形の数なので、
白8…(8-4)÷4=1個
白16…(16-4)÷4=3個
白32…(32-4)÷4=7個
白64…(64-4)÷4=15個
白128…(128-4)÷4=31個
白256…(256-4)÷4=63個
白512…(512-4)÷4=127個 ←100over!
したがって、1、3、7、15、31、63、127cm


コメント