問題PDF
同じ角材を2本と同じ木片をたくさん用意して、次の準備と実験1~6を行った。
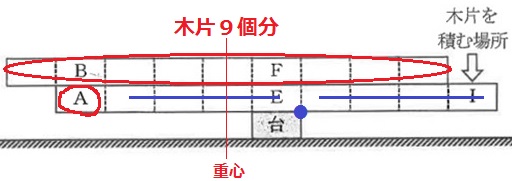
【準備】角材は重さが木片の9倍で、線を引いて9つに区分して、A、B・・・、Iと名前をつけた。実験は、いずれも水平な机の上に木片を1つ置いて台とし、その上に木片や角材をのせて行う。

【実験1】
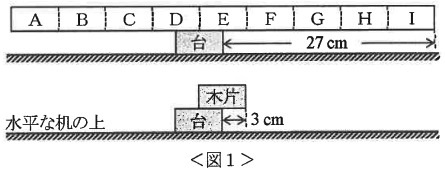
台の上に角材をのせた。台の右はしから角材の右はしまでの長さが27cmをこえると、角材はかたむいた(図1上)。次に、台の上に木片をのせた。台の右はしから木片の右はしまでの長さが3cmをこえると、木片はかたむいた(図1下)。
【実験2】
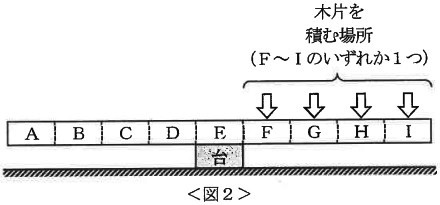
Eが台の上に重なるように角材をのせた(図2)。次に、F~Iのいずれかを1つ選び、その上に重なるように木片を積んでいく。その結果、Fを選んだ場合は積んだ木片の数が( ① )になったところで角材はかたむいた。また、G、H、Iでは、積んだ木片の数がそれぞれ( ② )、( ③ )、( ④ )になったところで角材はかたむいた。
【実験3】
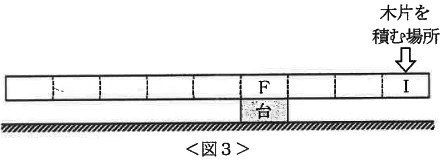
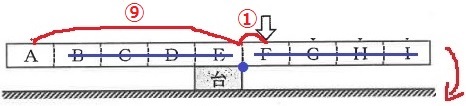
Fが台の上に重なるように角材をのせると、角材はかたむいた。そこで、Iの上に重なるように木片を積んで調整すると、積んだ木片の数が( ⑤ )~( ⑥ )のときだけ、角材は水平のままだった(図3)。
【実験4】
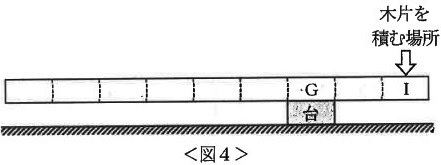
Gが台の上に重なるように角材をのせると、角材はかたむいた。そこで、Iの上に重なるように木片を積んで調整すると、積んだ木片の数が( ⑦ )~( ⑧ )のときだけ、角材は水平のままだった(図4)。
【実験5】
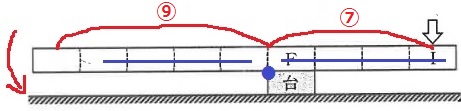
Eが台の上に重なるように角材をのせた。その上にもう1本の角材のFが台の上に重なるように、また、下の角材のAと上の角材のBが重なるようにのせると、2本の角材は水平のままだった(図5)。そこで、下の角材のIの上に重なるように木片を積んでいくと、木片の数が( ⑨ )になったところで、角材はかたむいた。

【実験6】
Eが台の上に重なるように角材をのせた。その上にもう1本の角材のIが台の上に重なるように、また、下の角材のAに上の角材のEが重なるようにのせると、角材はかたむいた。そこで、下の角材のIの上に重なるように木片を積んで調整すると、積んだ木片の数が( ⑩ )~( ⑪ )のときだけ、角材は水平のままだった(図6)。

続けて、木片の数が(⑪)のまま、以下の2つの操作を行った。
〔操作1〕
上にのせた角材だけを右に少しずつ動かした(図7)。すると、動かした長さが( ⑫ )cmをこえたところで、角材はかたむいた。

〔操作2〕
上にのせた角材だけを左に少しずつ動かした(図8)。すると、動かした長さが( ⑬ )cmをこえたところで、角材はかたむいた。

(1)
【実験2】の文中の①~④に入る整数をそれぞれ答えなさい。
(2)
【実験3】と【実験4】の文中の⑤~⑧に入る整数をそれぞれ答えなさい。
ただし、⑤<⑥、⑦<⑧とする。
(3)
【実験5】と【実験6】の文中の⑨~⑪に入る整数と、⑫と⑬に入る値をそれぞれ答えなさい。
ただし、⑩<⑪とする。
@解説@
過去問にも類題がでている。
(1)①…10、②…4、③…2、④…2
木片にも重さはある。
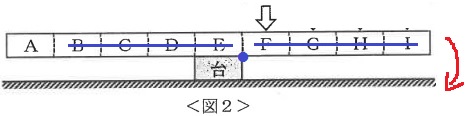
Fに木片を積んでいくと右に傾くので、支点は台の右上●で考える。
B~EとF~Iは支点をはさんで同じだから、これらを相殺しておく。
残ったAの支点●から重心までの距離を考える。
図1より重心は木片の真ん中。
計算しやすいように木片1つの横の長さを②とすると、
支点からFの重心までの長さは①、支点からAの重心までの長さは⑨。
A:F=⑨:①
→Aは木片1個。1×⑨(A)=9×①(F)
Fに木片9個積んだら角材は水平。10個目で右に傾く。
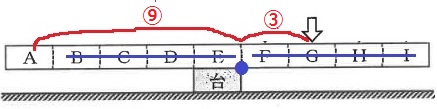
以下、同様。
支点●は台の右上。左右で同じ部分を相殺。
Gの場合、支点から重心までの距離は、A:G=⑨:③=③:①
1×③(A)=3×①(G)
Gに3個乗せると水平。4個目で右に傾く。
Hの場合は、A:H=⑨:⑤
Hに2個乗せると2×⑤=10で9をオーバー、右に傾く。
Iの場合は、A:I=⑨:⑦
Iに2個乗せると2×⑦=14で9をオーバー、右に傾く。
(2)⑤…2、⑥…5、⑦…6、⑧…15
下限から考える。
Iに木片を乗せないと左に傾くので、支点は台の左上。
左右の4個分の相殺。
支点と重心の距離は、左:右=⑨:⑦
Iに2個乗せると左に傾かなくなる。

上限を考える。
Iに乗せすぎると右に傾くので、支点は台の右上。
左右で3個ずつ相殺。
左は3つ余るので支点からの距離を合計する。
⑪+⑨+⑦=㉗
左:右=㉗:⑤
5個まではセーフ。
6個乗せると6×⑤=30で27をオーバー⇒右に傾く。

原理がわかってしまえば、あとは時間との勝負。
下限は台の左上が支点。3個ずつ相殺。
左:右=㉗:⑤
6×⑤=30で27を超すので下限は6個。
上限は台の右上支点で2個ずつ相殺。
左:右=㊺:③=15:1
15個目までセーフ。16個目から右に傾く。
(3)⑨…6、⑩…6、⑪…12、⑫…2、⑬…3
支点は台の右上で、4個ずつ相殺。
2階部分の木片9個分を重心に集める。左側は2階の角材と1階のAが残る。
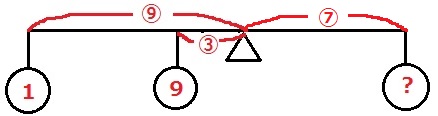
簡略するとこんな感じ。
?=(1×⑨+9×③)÷⑦=36/7
?が木片36/7個分で左右がつり合うから、6個目で右に傾く。

まずは下限から。支点左で4個ずつ相殺。
9×⑦÷⑨=7個
右のIは相殺しきれていないので-1すること!
積むべき木片の数は6個。

時間が足りないのでサクサクいきたい。
右に支点で4個ずつ相殺。
左は支点から⑨のところに10個分。
10×⑨÷⑦=90/7
90/7個分の木片で左右がつり合う。
90÷7=12…6なので、12個目まで水平。

具体的な長さを求めるので割合をやめる。
2階部分を右にズラすから支点は右側、4個ずつ相殺。
初期状態では支点から27cmのところに木片10個分の重さがかかっている。
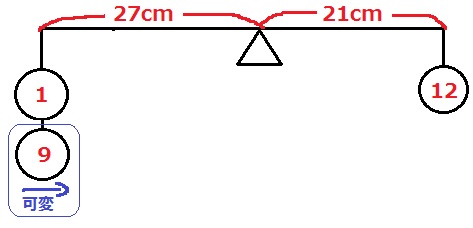
9個の木片が可変なので、これを右側にいくつズラすとつり合うか。
以下、木片の個数を〇で表す。
(⑫×21-①×27)÷⑨=25cm
木片9個を27-25=2cm右にズラすとつり合う。それを超えると右に傾く。
・・・・

左に傾く、左支点。
4つずつ相殺。⑬×27÷⑨=39cm
39-21=18cmで何度計算しても18なのに、四谷大塚の答えは3。
『四谷間違ったか?( ゚A゚)ダサー』って思ったら、

これがあった・゚・(゚`Д´゚)・゚・
1階Aの左端に2階の重心、すなわち、2階Eの真ん中がくればよいので、
四谷の言うとおり、左3cmを超すと2階部分だけが落ちます。


コメント