2022年度　和歌山県公立高校入試問題過去問【数学】解説

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）①
－９＋４
＝－５

②
10/３＋２÷（－３/４）
＝10/３－８/３
＝２/３

③
（３ａ＋５ｂ）＋２（２ａ－ｂ）
＝３ａ＋５ｂ＋４ａ－２ｂ
＝７ａ＋３ｂ

④
√48－√３＋√12
＝４√３－√３＋２√３
＝５√３

⑤
（ａ＋３）²－（ａ＋４）（ａ－４）
＝ａ²＋６ａ＋９－ａ²＋16
＝６ａ＋25

（２）
ｘ²＋５ｘ－14
＝（ｘ＋７）（ｘ－２）＝０
ｘ＝－７、２

（３）
根号の中の数とｎが同じであれば、約分して自然数になる。
√20＝２√５

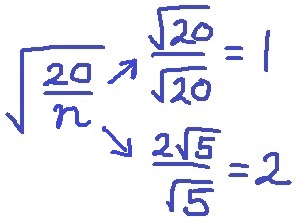
この２通りしかない。
ｎ＝５、20

（４）
反比例の比例定数ａはｘとｙの積である20。
ｙ＝20/ｘ
これにｘ＝－10を代入して、ｙ＝－２

（５）

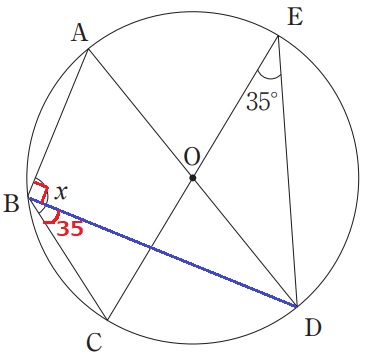
ＢＤに補助線。
孤ＣＤに対する円周角で、∠ＣＢＤ＝35°
直径ＡＤに対する円周角で、∠ＡＢＤ＝90°
ｘ＝35＋90＝125°

（６）
半径４ｃｍの半球。
【球の体積Ｖ＝４/３πｒ³】
４/３π×４³÷２＝128/３πｃｍ³

大問２（小問集合２）

（１）
玉を取り出す作業だが、ようはＡ～Ｄの４人の走る順番を考えればいい。
全体の場合の数は、₄Ｐ₄＝24通り
Ａが１番で、Ｄが４番→【ＡＢＣＤ】か【ＡＣＢＤ】しかない。
確率は、２/24＝１/12

（２）①
オリンピック問題。

１ループはどこからどこまでか⇒１～10番目。
27÷10＝２…７
余り７は黄色。

②
124÷10＝12…４
12ループと余り４。
１ループに黒は２つ、余り４に１つ。
２×12＋１＝25個

（３）
答案では過程も記述する。
唐揚げ弁当１個の定価をｘ円、エビフライ弁当１個の定価をｙ円とする。
ｘ＋50＝ｙ　…①

唐揚げ弁当は10個はｘ円、残りの10個は0.5ｘ円で販売。
エビフライ弁当は20個すべてｙ円で販売した。
10ｘ＋0.5ｘ×10＋20ｙ＝15000
15ｘ＋20ｙ＝15000　…②

①を②に代入すると、
15ｘ＋20（ｘ＋50）＝15000
35ｘ＝14000
ｘ＝400
①に代入して、ｙ＝450
唐揚げ弁当…400円、エビフライ弁当…450円

（４）①

Ⅰ：四分位範囲＝第３四分位数（Ｑ3）－第１四分位数（Ｑ1）でＣが最も大きい。×
Ⅱ：第２四分位数（Ｑ2；中央値）をみるとＢだけ20冊以下。Ｂの過半数が20冊以下。〇
Ⅲ：Ａの最大値は30～35冊である。
ＣのＱ3は上位17人の中央値、すなわち、上から９番目の生徒が30～35冊である。
しかし、Ｂはわからない。△
Ⅰ…イ、Ⅱ…ア、Ⅲ…ウ

②
わかりやすいところから除外していく。
エは最小値と最大値が違う。
Ｃ組34人のＱ2は17番目と18番目の平均で、Ｑ1は下から９番目、Ｑ3は上から９番目。
イはＱ1とＱ3が違う。
アのＱ2は15～20冊の階級にあって違う。
ウ

③
無作為に抽出した標本といえないから。
*３年生の生徒だけから抽出したら、あくまで３年生の結果になる。
これでは１～３年生までの全校生徒を調べたことにはならない。
標本（サンプル）は学年や性別といった属性に偏ることなく、無作為に抽出する。

大問３（関数）

（１）
ｙ＝ａｘ²において、ｘの値がｐ→ｑまで増加するときの変化の割合はａ（ｐ＋ｑ）。
１/４×｛（－２）＋０｝＝－１/２

（２）
ｙ＝１/４ｘ²は下に凸のグラフ。
ｘ＝０のとき、最小値ｙ＝０
最大値ｙ＝９、１/４ｘ²＝９
ｘ＝±６
ｘ≧－２だから、ｘ＝６
ア…６、イ…０

（３）

二等辺三角形ＯＰＢの等辺は４パターンある。
このうち、ｘ座標が最も小さいのはＢ1で、最も大きいのはＢ4。

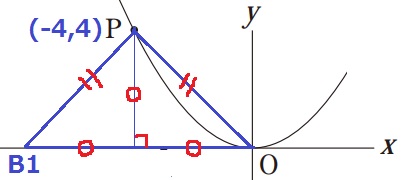
Ｐから垂線をおろして〇＝４。Ｂ1のｘ座標は－８。

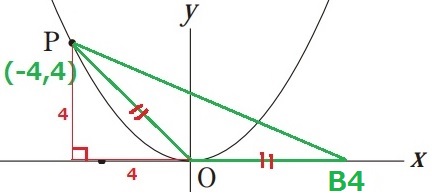
三平方でＰＯ＝４√２
Ｂ4のｘ座標は４√２。
最も大きい…Ｂ（４√２、０）、最も小さい…Ｂ（－８、０）

（４）

△ＯＰＤ：△ＯＤＣ＝３：２から、ＰＤ：ＤＣ＝③：②
Ｐ・Ｄ・Ｃのｘ座標の差より、Ｐのｘ座標は－６。
これをｙ＝１/４ｘ²に代入して、Ｐ（－６、９）

なんとなくＰＣとＡＯが平行っぽく見える・・。
Ｐ⇒Ｃは右に10、下に５で傾き－１/２。
Ａ⇒Ｏは右に２、下に１で傾き－１/２。
ＰＣ//ＡＯより、四角形ＯＡＰＣは台形である。

各々の点のｘ座標の差から、ＡＯ＝②、ＰＣ＝⑩とすると、
上底と下底の和である⑫を⑥ずつに分ける直線を考えればいい。

ちょうどＤを通過する。
ＰとＣのｙ座標の差である５を３：２に内分してＤ（０、６）。
Ａ⇒Ｄは右に２、上に５だから傾きは５/２。
ｙ＝５/２ｘ＋６

大問４（平面図形）

（１）①

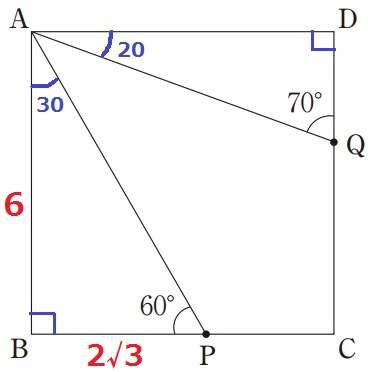
三角形の内角より∠ＢＡＰ＝30°、∠ＤＡＱ＝20°
∠ＰＡＱ＝90－（30＋20）＝40°

②
△ＡＢＰの内角は30°―60°―90°で辺の比は１：２：√３。
ＢＰ＝６×１/√３＝２√３ｃｍ
△ＡＢＰの面積は、２√３×６÷２＝６√３ｃｍ²

（２）
定番の形である。

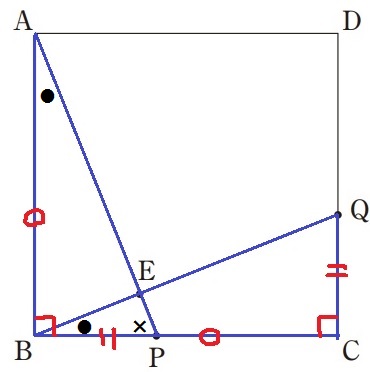
仮定よりＢＰ＝ＣＱ
正方形ＡＢＣＤよりＡＢ＝ＢＣ、∠ＡＢＰ＝∠ＢＣＱ
２辺とあいだの角が等しいから、△ＡＢＰ≡△ＢＣＱ

∠ＰＡＢ＝●、∠ＡＰＢ＝×として、△ＡＢＰの内角から●＋×＝90°
対応する角で∠ＱＢＣ＝∠ＰＡＢ＝●
△ＢＰＥで外角定理→∠ＡＥＢ＝●＋×＝90°

（３）
前問と少しかぶっている。

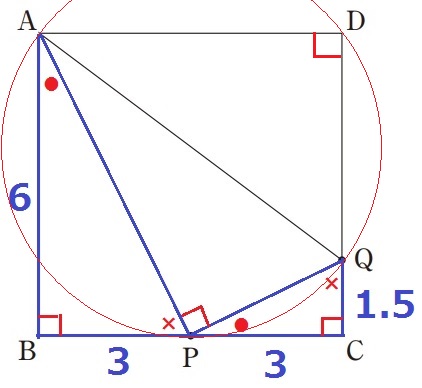
∠ＢＡＰ＝∠ＣＰＱ＝●とする。
∠ＡＢＰ＝∠ＰＣＱ＝90°とあわせて２角相等→△ＡＢＰ∽△ＰＣＱ
ＡＢ：ＢＰ＝ＰＣ：ＣＱ＝２：１
ＣＱ＝３÷２＝1.5ｃｍ

円の直径は直角探し。
∠ＡＰＢ＝×として、△ＡＢＰの内角より●＋×＝90°
∠ＡＰＱ＝180－（●＋×）＝90°
３点Ａ、Ｐ、Ｑを通る円の直径はＡＱである。
（∠ＡＤＱ＝90°からＤも同一円周上にある）

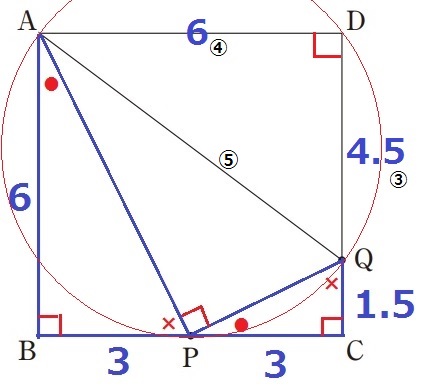
ＤＱ＝６－1.5＝4.5ｃｍ
△ＡＤＱに着目すると、ＡＤ：ＤＱ＝６：4.5＝④：③
△ＡＤＱは辺の比が３：４：５の直角三角形。
ＡＱ＝６×⑤/④＝15/２ｃｍ
したがって、円の半径は15/４ｃｍ。