2022年度　秋田県公立高校入試問題過去問【数学】解説

平均55.5点（前年比；＋4.8点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

*15問の中から指示された８問を解答する。
（１）　91.0％
－３×（５－８）
＝－３×（－３）
＝９

（２）　90.2％
ａ²×ａｂ²÷ａ³ｂ
＝ｂ

（３）　71.8％
√80×√５
＝√400＝20

（４）　64.4％
無理数は整数の分数で表せない数。
√９＝３＝３/１
－0.6＝－３/５
無理数は√２、π。
*円周率πは循環しない無限小数ゆえ分数で表せない。

（５）　74.0％
ｘ＋ｙ＝９ …①
0.5ｘ－１/４ｙ＝３
これを４倍すると、２ｘ－ｙ＝12　…②
①＋②をしてｘ＝７
①に代入してｙ＝２
ｘ＝７、ｙ＝２

（６）　73.7％
ｘ²＋３ｘ＋２
＝（ｘ＋２）（ｘ＋１）＝０
ｘ＝－２、－１

（７）　85.5％
反比例の比例定数ａは積ｘｙの８。
ｙ＝８/ｘ

（８）　84.5％
白は60個中18個の割合。
500×18/60＝150個

（９）　64.9％
25ｘ²－ｙ²
＝（５ｘ＋ｙ）（５ｘ－ｙ）　←ここで代入
＝（５×11＋54）（５×11－54）
＝109×１＝109

（10）　9.7％!!
中学受験によくでてくるスタイル。
148÷ｎ＝〇…４
245÷ｎ＝△…５
ｎ×〇＝148－４＝144
ｎ×△＝245－５＝240
144と240はともにｎの倍数である。

144と240の公約数を調べる。
最大公約数は48。
ｎは48の約数である。
【１・２・３・４・６・８・12・16・24・48】
このうち、割る数は余りの５より大きいから【６～48】の６個。

（11）　93.4％

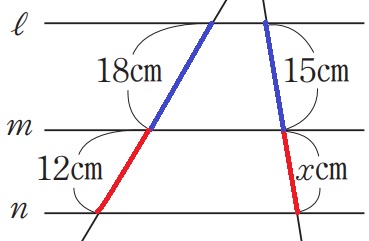
平行線と線分の比。
18：12＝15：ｘ
ｘ＝12×15/18＝10

（12）　71.1％

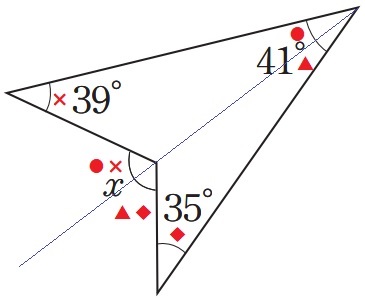
ブーメランの３つの角の和は股の角。
外角定理を上下に適用して、
ｘ＝39＋41＋35＝115°

（13）　88.7％

赤線が答え。
Ａ・Ｂ・Ｃ・Ｄの位置はわかりやすい。
ＤＨを共有する面は面ＡＤＨＥと面ＣＤＨＧ。
ここからＨとＧの位置がわかる。
４つの側面にはＤ→Ｈ→Ｇ→Ｃ→Ｄ、Ａ→Ｅ→Ｆ→Ｂ→Ａが一列で並ぶ。

（14）　20.4％！
円錐の中心角は半径/母線。
円錐の側面積は、母線×母線×π×半径/母線＝母線×半径×π

母線×３×π＝24π
母線＝８ｃｍ
三平方の定理より、円錐の高さは、√（８²－３²）＝√55ｃｍ
円錐の体積は３×３×π×√55÷３＝３√55πｃｍ³

（15）　7.7％!!
大問１だが難しい(;^ω^)

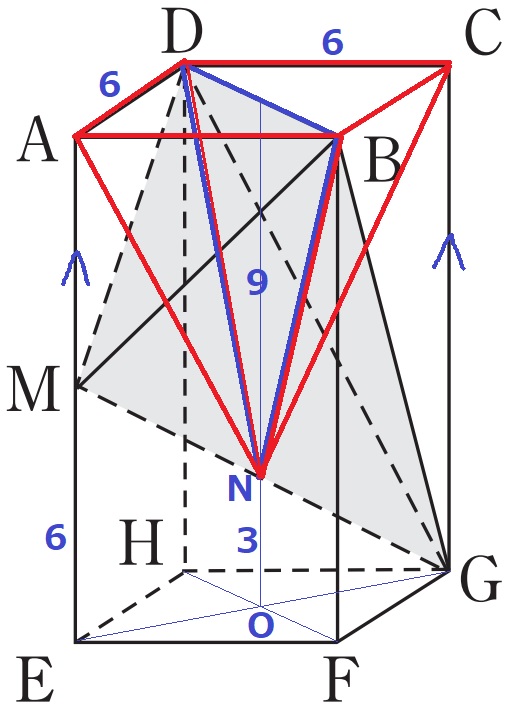
ＨＦ、ＥＧの交点をＯとし、Ｏの真上にあるＭＧとの交点をＮとする。
面ＮＢＤがＡＭとＣＧと平行である点に注目してＭ⇒Ａ、Ｇ⇒Ｃに移動させると、
等積変形により四面体ＢＤＧＭは正四角錘Ｎ—ＡＢＣＤに変形できる。

△ＭＧＥ∽△ＮＧＯより、ＮＯ＝６÷２＝３ｃｍ
正四角錘の高さは12－３＝９ｃｍ
したがって、体積は６×６×９÷３＝108ｃｍ³

大問２（小問集合２）

（１）①　47.2％
２ｘ＋３ｙ＝－６
ｙ＝－２/３ｘ－２

切片は（０、－２）
右に３、下に２の傾きで格子点を通過するように描く。

②　78.2％
右上なので傾きａ＞０
切片ｂ＜０
イ

（２）①　77.3％
ｙ＝ｘ²とｙ＝－１/２ｘ²にｘ＝２を代入。
Ｂのｙ座標は４、Ｃのｙ座標は－２。
ＢＣ＝４－（－２）＝６ｃｍ

②　4.9％!!

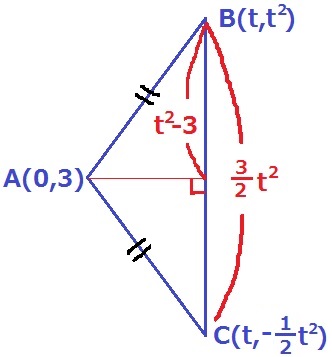
Ｂのｘ座標をｔとする。
Ｂ（ｔ、ｔ²）Ｃ（ｔ、－１/２ｔ²）
ＢＣ＝ｔ²－（－１/２ｔ²）＝３/２ｔ²

もう１つは二等辺三角形の性質を利用する。
頂角Ａから底辺ＢＣに向けて垂線をひくと、交点はＢＣの中点を通る。
ＢＣ＝２（ｔ²－３）＝２ｔ²－６

ＢＣの長さで等式。
３/２ｔ²＝２ｔ²－６　←２倍
３ｔ²＝４ｔ²－12
ｔ²＝12
ｔ＞０より、ｔ＝２√３

（３） 55.5%

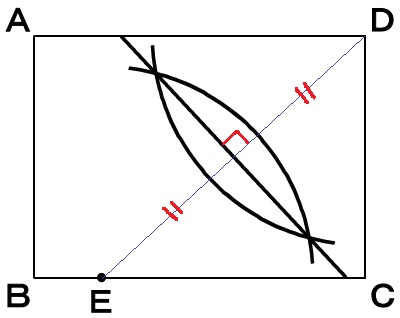
ＤとＥが対応する点となるような対称の軸が折り目になる。
⇒ＤとＥの垂直二等分線
折り目なので長方形ＡＢＣＤの端から端まで描く。

（４） 52.3%

高さは４ｃｍのままなので一次関数で増減する。
０≦ｘ≦４では上底と下底がともに伸びる。
ｘ＝４のとき、ｙ＝24

４≦ｘ≦８では上底の増加より下底の減少が上回るので、面積は減少する。
ｘ＝８のとき、ｙ＝16
エ

大問３（規則）

（１）①　74.8％

Ａは１、３、６、10…（＋２、＋３、＋４…）と三角数が連なる。
ＢはＡの１個手前が連なる。
ア…28、イ…21
*ちなみに、ＡとＢの和は平方数になる。

②　21.0％！

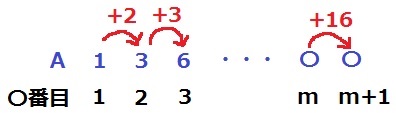
Ａの数と〇番目の関係を整理する。
＋２して２番目、＋３して３番目だから、＋16したｍ＋１は16番目。
ｍ＝15

③　9.3％!!

１段目は左の三角形が１個で、右の三角形がｍ個だから和はｍ＋１個。
２段目は左が２個で、右がｍ－１個だから和はｍ＋１個。
各段のＡはｍ＋１個→ｍ段あるから全体のＡはｍ（ｍ＋１）個。

左右の三角形は合同なので、半分にすればもとの図形のＡの数がでる。
｛ｍ（ｍ＋１）｝/２個
ウ…ｍ（ｍ＋１）、エ…｛ｍ（ｍ＋１）｝/２
*等差数列の和の公式である。
１からｎまでの自然数の和→１/２ｎ（ｎ＋１）

（２）　28.1％！
今までと違った視点でみないと見えてこない。
正六角形をどううまく切り分けるか。

このような回転対称（回転させたら元と同じになる図形）で分けると計算がしやすい。
１つの固まりにおいて、Ａの数が〇番目の平方数になっている。
ｎ番目であれば、ｎ²×３＝３ｎ²個

＠別解＠

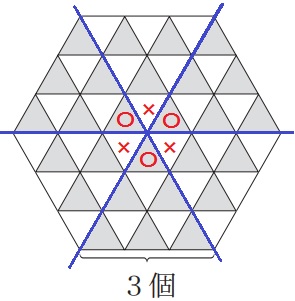
正六角形というと、この区切り方が想像されやすいと思う。
しかし、３ピースの頂点はＡから始まるが、残りの３ピースはＢから始まる。

ＢはＡよりワンテンポ遅れる。ＡとＢの位置関係が逆になると、
前問の｛ｎ（ｎ＋１）｝/２のｎをｎ－１に変えて、｛ｎ（ｎ－１）｝/２になる。

*分配法則を利用しましょう。

＠追記＠

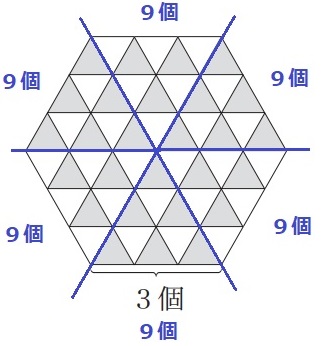
もしくはＡとＢを一体して見るのも良い。
１ピースあたりの和はｎ番目の平方数だから３²＝９個
これが６ピースあるので６×９＝54個
全体を一体してみると、ＡとＢの数は同じである。
54÷２＝27個
ｎでやると、ｎ²×６÷２＝３ｎ²個

大問４（確率・データの活用）

（１）①　88.8％
２か４を出す。
２/４＝１/２

②　39.4％
答案では根拠となる数値を示して理由を説明する。
【Ａ】取り出した１枚を戻さずにもう１枚取る。
⇒一度に２枚取るのと同じ。
すべての取り方は、₄Ｃ₂＝６通り
和が５以上の組み合わせは、（４、１～３）（３、２）の４通り。
確率は４/６＝２/３

【Ｂ】取り出した１枚を戻し、再び１枚取る。
全体は４×４＝16通り
一度４を出すと５以上が確定なので、余事象から攻めた方が良い。
５未満の組み合わせは、（１、３～１）（２、２～１）（３、１）の６通り。
５以上は、16－６＝10通り
確率は10/16＝５/８
２/３＞５/８なので、Ａの方が起こりやすい。

（２）　65.0％
ア：10個ずつなので、度数の大きいＱの方が相対度数は大きい。×
イ：Ｐ３個、Ｑ４個。×
ウ：最頻値（モード）は最もあらわれている値。Ｐ57ｇ、Ｑ55ｇ。×
エ：10個の中央値（メジアン）は５番目と６番目の平均。Ｐ57ｇ、Ｑ55ｇ。〇
エ

大問５—Ⅰ（平面図形）

（１）　49.0％
△ＡＢＣ∽△ＡＣＤの証明。

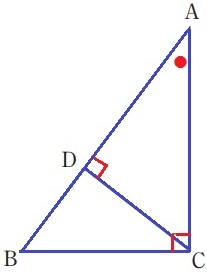
共通角＋仮定の90°→２角相等で∽。

（２）①　73.8％
弧ＡＥに対する円周角より、∠ＡＢＥ＝∠ＡＣＥ
ウ

②　2.4％!!

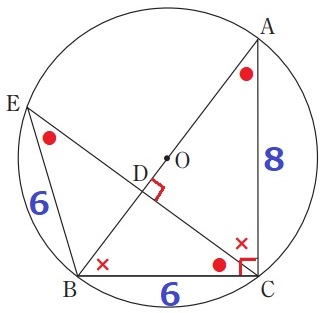
●＋×＝90°で角度を調査。
∠ＡＣＤ＝×とすると、∠ＢＣＤ＝90－×＝●
２角相等で△ＡＢＣ∽△ＣＢＤ

また、孤ＢＣに対する円周角で、∠ＢＥＣ＝∠ＢＡＣ＝●
△ＢＣＤは底角が等しく、二等辺三角形。
ＢＣ＝ＢＥ＝６ｃｍ
△ＡＢＣで三平方→辺の比は３：４：５でＡＢ＝10ｃｍ
△ＡＢＣ：△ＣＢＤの相似比は、ＡＢ：ＣＢ＝５：３
面積比は相似比の２乗→25：９
△ＢＣＤは△ＡＢＣの９/25倍。

大問５—Ⅱ（平面図形）

（１）　38.2％
△ＡＢＣ∽△ＡＤＢの証明。

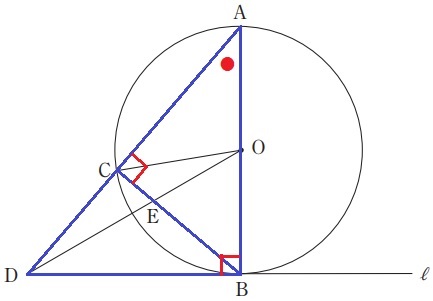
半円の弧に対する円周角で、∠ＡＣＢ＝90°
接線と半径は直交するので、∠ＡＢＤ＝90°
これと共通角●をあわせ、２角相等で∽。

（２）①　47.2％

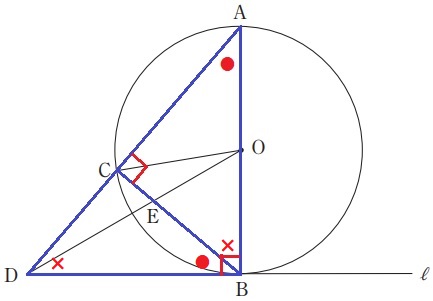
●＋×＝90°で角度調査。
∠ＡＢＣ＝×とすると、∠ＣＢＤ＝90－×＝●
∠ＢＡＤ＝∠ＣＢＤ
イ
*接弦定理でも指摘できる。

②　0.0％!!!
シンプルな構図だが出しにくい(´°ω°`;)

ＯＢ＝③、ＡＤ＝⑧とする。
半径でＡＯ＝③だから、ＡＢ＝⑥
ここで（１）の相似△ＡＢＣ∽△ＡＤＢを使う。
ＡＢ：ＡＣ＝ＡＤ：ＡＢ
ＡＣ＝⑥×６/８＝〇９/２
ＣＤ＝⑧－〇９/２＝〇７/２

ＡＣ：ＣＤ＝９/２：７/２＝⑨：⑦
△ＡＢＣ：△ＣＢＤの面積比も９：７。
ＡＯ＝ＯＢから△ＡＯＣと△ＯＢＣの面積は等しい。
面積比を整数にするため、△ＡＢＣ：△ＣＢＤ＝９：７＝⑱：⑭として
面積比を配分すると上図のようになる。

ここで△ＯＢＣと△ＣＢＤに注目する。
底辺ＣＢを共通とするので、高さの比にあたるＯＥ：ＥＤが面積比にあたる。
すなわち、ＯＥ：ＥＤ＝９：14

今度は視点を変えて、面積比を△ＯＢＥ＝⑨、△ＥＢＤ＝⑭で捉えなおす。
ＡＯ＝ＯＢより、△ＡＯＤ＝△ＯＢＤ＝㉓
△ＡＢＤ：△ＯＢＥ＝㊻：⑨
したがって、△ＯＢＥは△ＡＢＤの９/46倍。