2021年度　神奈川県公立高校入試問題過去問【数学】解説

平均58.2点（前年比；＋2.5点）

問題はコチラ→ＰＤＦファイル
出題範囲の除外は資料の活用（標本調査）
追試験の解説はコチラ（全体的に本試験より難易度高めです）

大問１（計算）
大問２（小問集合１）
大問３（小問集合２）
大問４（関数）
大問５（確率）
大問６（空間図形）

大問１（計算）

（ア）　96.4％
－９－（－５）
＝－９＋５
＝－４　【２】

（イ）　92.7％
－５/６－３/４
＝－19/12　【１】

（ウ）　95.7％
８ａｂ²×３ａ÷６ａ²ｂ
＝４ｂ　【３】

（エ）　88.7％
（３ｘ＋２ｙ）/５－（ｘ－３ｙ）/３
＝｛３（３ｘ＋２ｙ）－５（ｘ－３ｙ）｝/15
＝（４ｘ＋21ｙ）/15　【３】

（オ）　90.3％
（２＋√７）（２－√７）＋６（√７＋２）
＝４－７＋６√７＋12
＝９＋６√７　【４】

＠＠
共通因数でくくることもできるが、そのまま計算した方が早い。
（２＋√７）（２－√７）＋６（√７＋２）
＝（２＋√７）（２－√７＋６）
＝（２＋√７）（８－√７）
＝16＋６√７－７
＝９＋６√７

大問２（小問集合１）

（ア）　92.3％
（ｘ＋６）²－５（ｘ＋６）－24　←（ｘ＋６）をＸに置き換え
＝Ｘ²－５Ｘ－24
＝（Ｘ－８）（Ｘ＋３）　←Ｘを（ｘ＋６）に戻す
＝（ｘ＋６－８）（ｘ＋６＋３）
＝（ｘ－２）（ｘ＋９）　【４】

（イ）　93.9％
ｘ²－３ｘ＋１＝０
解の公式を適用。
ｘ＝（３±√５）/２　【２】

（ウ）　85.2％
ｙ＝ａｘ²のグラフでｘの値がｐ→ｑに増加するときの変化の割合はａ（ｐ＋ｑ）
ａ（１＋４）＝－３
ａ＝－３/５

（エ）　80.0％
200ｋｇ以上なので200を含む。　【１】

（オ）　86.2％
540を素因数分解すると、
540＝２²×３³×５
各素因数が偶数個になれば平方数となり、根号が外れる。
３を１個、５を１個減らせばいい。
ｎ＝３×５＝15　【３】

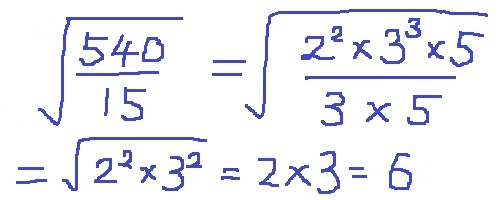
指数は割り算では引き算。

（カ）　46.8％
なかなか出しにくい(´ﾟωﾟ`;)

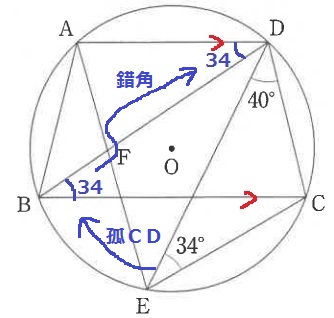
弧ＣＤに対する円周角と錯角で34°を移動。

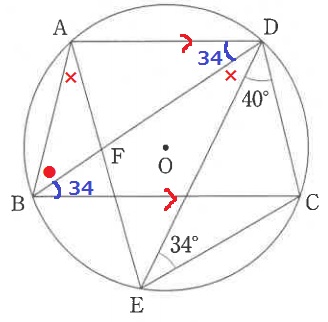
孤ＢＥに対する円周角の∠ＢＡＥ＝∠ＢＤＥ＝×、∠ＡＢＤ＝●とおく。
円に内接する四角形の対角の和は180°であるから、
（●＋34）＋（34＋×＋40）＝180°
●＋×＝72°
△ＡＢＦで外角定理→∠ＡＦＤ＝●＋×＝72°　【１】

大問３（小問集合２）

（ア）ⅰ　ａｂ…88.2％、ｃ…88.7％
△ＡＤＦ≡△ＣＦＥの証明。

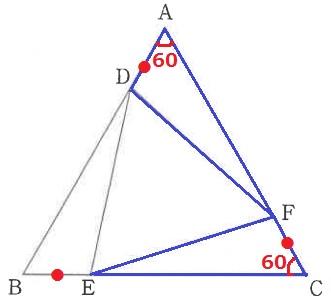
仮定より、ＡＤ＝ＣＦ（●）
△ＡＢＣは正三角形だから、∠ＤＡＦ＝∠ＦＣＥ＝60°
（正三角形の１辺）－●から等式を立てる。
ＡＦ＝ＣＡ－ＣＦ（●）
ＣＥ＝ＢＣ－ＢＥ（●）
よって、ＡＦ＝ＣＥ
以上より、２辺とあいだの角が等しく合同。
ａ…【４】、ｂ…【１】、ｃ…【２】

ⅱ　7.8％!!

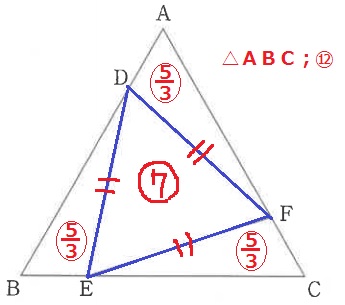
対称性から、△ＡＤＦ≡△ＣＦＥ≡△ＢＥＤ
（ＤＥ＝ＥＦ＝ＦＥより、△ＤＥＦは正三角形）
△ＡＢＣの面積を⑫、△ＤＥＦの面積を⑦とすると、
周囲の３つの三角形は、（⑫－⑦）÷３＝〇５/３

分数がわずらわしいので、３倍して整数値になおしてみる。
すると、△ＡＢＣの面積は㊱でちょうど平方数。
㊱＝【６】×【６】

正三角形の１辺の長さを【６】とする。
周囲の３つの三角形の面積は隣辺比で⑤＝【１】×【５】
【１】＋【５】＝【６】で正三角形ＡＢＣの１辺【６】と符合する。
ＡＤ：ＤＢ＝【１】：【５】
ＡＤ＝18×１/６＝３ｃｍ

＠＠

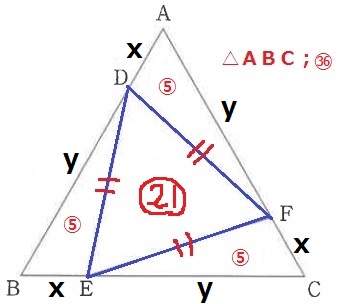
偶然に出ちゃった感がありますけど(;^ω^)
数学っぽくやるのであれば、ＡＤ＝ｘ、ＤＢ＝ｙとおいて、
ｘ＋ｙ＝６、ｘｙ＝５で方程式でしょうか。
本問はあてはめてしまった方が早いと思います。

（イ）　32.9％！
縦軸が相対度数になっている。
あ：相対度数の和が0.50を超える階級がどこかを調べる。
縦軸の１目盛りは0.02。
Ａ；0.01＋0.02＋0.09＋0.21＋0.24＝0.57→20～25ｃｍ
Ｂ；０＋0.04＋0.12＋0.22＋0.24＝0.62→20～25ｃｍ
階級値はともに22.5ｃｍで同じ。〇

い：先ほどの計算式を利用しよう。
Ａ；0.33　Ｂ；0.38　Ａの方が小さい×

う：ＡとＢで人数が異なる点に注意。
Ａ；100×0.24＝24人　Ｂ；150×0.24＝36人　Ｂの方が多い〇
*割合が同じであれば、人数の多いＢの方が多い。

え：ＡとＢの対比でなく、それぞれのなかで比較するので相対度数で比べる。
Ａ；25～30ｍ…0.26　30ｍ以上…0.15＋0.02＝0.17
Ｂ；25～30ｍ…0.18　30ｍ以上…0.16＋0.04＝0.20
Ｂは30ｍ以上の生徒の人数の方が多い。×
〔あ・う〕が正しい。【２】

（ウ）ⅰ　52.3％
ＰからＱに水が流れ始める時間を求める。
Ｐ側の体積を200ｃｍ³で割ればいい。
ａ＝30×40×18÷200＝108

ⅱ　62.9％
高さ18ｃｍになるのは108秒後。３か４に絞られる。

Ａ→Ｂ→Ｃの順で満たされる。
底面積の比がＡ：Ｂ＝40：20＝２：１だから、時間の比は②：①。
Ｂの時間はＡの半分。Ｃではさらに底面積が増えるので、傾きは緩やかになる。
【３】

（エ）　33.1％！
先週の利用者数の合計より、
ｘ＋ｙ＝580　…①
増加した人数で立式。
ｘの１割→0.1ｘ、ｙの３割→0.3ｙ
0.1ｘ＋0.3ｙ＝92　…②
②の式を10倍。
ｘ＋３ｙ＝920　…③

③－①
ｘ＋３ｙ＝920
－) ｘ＋ｙ＝580
２ｙ＝340
ｙ＝170
①より、ｘ＝580－170＝410
先週の大人が410人。
今週の大人は１割増だから、410×11/10＝451人
ⅰ…0.1ｘ＋0.3ｙ、ⅱ…410、ⅲ…451

2020年度　豊島岡女子学園高校過去問【数学】大問４解説

問題ＰＤＦある中学校の合唱部の2017年の部員数は、女子がｘ人、男子が64人でした。2018年の部員数は、2017年と比べて女子がｙ％減り、男子がｙ％増えました。2019年の部員数は、2018年と比べて女子が40％増え、男子がｙ％減りました...

ややハイレベルな設問を置いておきます。

大問４（関数）

（ア）　85.5％
ｙ＝－ｘから、Ａ（－５、５）
これをｙ＝ａｘ²に放り込む。
５＝25ａ
ａ＝１/５　【４】

（イ）　46.5％

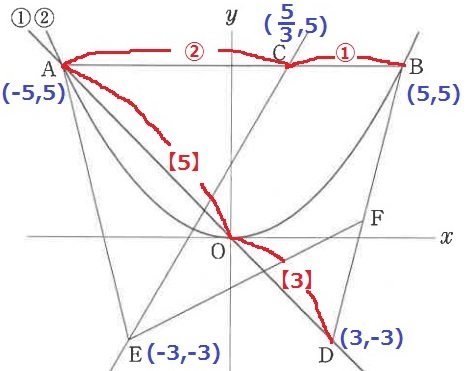
まずは座標を調べていく。
ＡＣ：ＣＢ＝２：１より、Ｃのｘ座標は、５－10×①/③＝５/３
Ｃ（５/３、５）
ＡＯ：ＯＤ＝５：３より、Ｄ（３、－３）
Ｅはｙ軸についてＤに対称だからＥ（－３、－３）
Ｃ（５/３、５）とＥ（－３、－３）を通るグラフの式を求める。
５＝５/３ｍ＋ｎ
－)－３＝－３ｍ＋ｎ
８＝14/３ｍ
ｍ＝８×３/14＝12/７
ｎ＝５－５/３×12/７＝15/７
ⅰ…【４】、ⅱ…【６】

（ウ）　5.6％!!

ＡＣ：ＣＢ＝２：１
△ＡＣＥの面積を②とすると、△ＢＣＥは①。
四角形ＢＣＥＦの面積が②だから、△ＥＦＢは②－①＝①

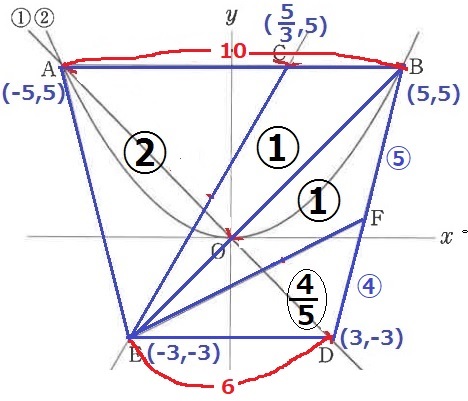
ＥＤに補助線。
△ＡＢＥ：△ＥＤＢ＝10：６＝５：３
△ＥＤＢ＝③×３/５＝〇９/５
△ＥＤＦ＝〇９/５－①＝〇４/５
ＤＦ：ＦＢ＝△ＥＤＦ：△ＥＦＢ＝４/５：１＝④：⑤

Ｆのｘ座標は、３＋（５－３）×④/⑨＝35/９
Ｆのｙ座標は、－３＋｛５－（－３）｝×④/⑨＝５/９
Ｆ（35/９、５/９）

大問５（確率）

（ア）　44.5％
操作２から考える。
１～６の数字のなかで、約数が４つあるのは６だけ（１・２・３・６）
→ｂ＝６が確定。
箱Ｑに１・２・３・６のカードが入っていなければならないので、
操作１で箱Ｐから１・２を調達する必要がある。
ａ＝３
（ａ、ｂ）＝（３、６）の１通りしかない。
確率は１/36　【１】

（イ）　11.9％！
ここも操作２のｂから考える。
約数をどこかにまとめておこう。
１⇒１
２⇒１・２
３⇒１・３
４⇒１・２・４
５⇒１・５
６⇒１・２・３・６

◆ｂ＝１のとき
箱Ｐから１を調達する。ａ＝１・３・５の３通り
◆ｂ＝２のとき
箱Ｐから１・２の１枚だけを調達。ａ＝１・２・５・６の４通り
◆ｂ＝３のとき
箱Ｑに３があるので、箱Ｐから１を調達してはならない。ａ＝２・４・６の３通り
◆ｂ＝４のとき
箱Ｐから１・２・４の１枚だけを調達。ａ＝１・２・４の３通り
◆ｂ＝５のとき
箱Ｑに５があるので、箱Ｐから１を調達してはならない。ａ＝２・４・６の３通り
◆ｂ＝６のとき
箱Ｑに３・６があるので、最低でも箱Ｒに２枚移ってしまう。×
計16通り。
確率は、16/36＝４/９

大問６（空間図形）

（ア）　69.1％

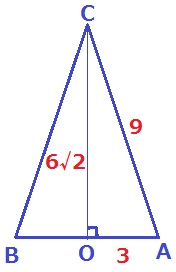
三平方で高さを算出→ＣＯ＝６√２ｃｍ
円錐の体積は、３×３×π×６√２÷３＝18√２πｃｍ³　【２】

（イ）　63.6％
側面積の扇形の面積＝半径×母線×π
３×３×π＋３×９×π＝36πｃｍ²　【５】

（ウ）　3.4％!!
最短距離なので展開図を作成。

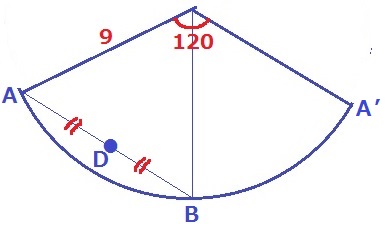
注意すべきは、ＡＢは円の半周であること。１周しない。
この手の問題は、だいたい有名角が潜んでいる。
扇形の中心角は、360×半径/母線＝360×３/９＝120°
ここからDを起点として円錐を１周したい。どう描写すべきか・・。

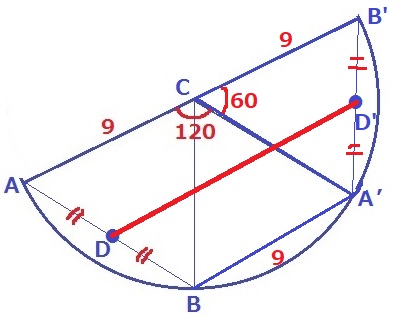
右側にもう１個追加。
ＡＢとＡ’Ｂ’が同一の辺で、その中点ＤとＤ’が同一だから、
赤線のＤ～Ｄ’が求めるべき１周の長さとなる。
ＡＢ’＝18ｃｍ
△Ａ’ＢＣは正三角形なので、Ａ’Ｂ＝９ｃｍ
ＡＤ：ＤＢ＝Ｂ’Ｄ’：Ｄ’Ａ’＝１：１
ＤＤ’はＡＢ’とＢＡ’の平均→（18＋９）÷２＝27/２ｃｍ

2021年度　滋賀県公立高校入試問題過去問【数学】解説

平均38.0点（前年比；－4.1点）問題はコチラ→ＰＤＦファイル出題範囲の縮小は資料の活用（標本調査）大問１（小問集合）（１）　93.4％２×（－３）＋１＝－６＋１＝－５（２）　88.6％５/３ａ－３/４ａ＝11/12ａ（３）　82.2％ｘ...

今年度の滋賀県でヒモをメガホンに２周巻きつける問題が出題されました。
大問２（４）です。

大問２
（オ）まで稼いでおきたい。
（カ）よくある形に見えて出しにくい。
円周角と錯角から等角を洗い出す。
大問３
（ア）辺の比がわかればよいので、隣辺比の和積で対処。
分母を払うと△ＡＢＣの面積比が平方数である点に着目する。
（イ）相対度数の出し方が特殊だが、終始小数の計算にウェイトがかかっており、
なんかヤダ(-_-;)
大問４
（ウ）ＥＤに補助線をひいて面積比をうまく使う。
等積変形でもできるが、それを利用しなくても解ける良い問題であった。
大問５
（イ）過不足なく調べ上げるのは大変(;´Д`A
解説ではｂの約数から何を調達すべきかで場合分けをしたが、ａでも整理できる。
大問６
前半は体積→表面積の流れ。いずれも小問集合レベル。
（ウ）大変面白い問題であった。
２本目の最短距離は、反射の問題に出てくる鏡の世界を利用した。

＠2021年度・神奈川解説＠
数学(追検査)　社会…平均72.6点　理科…平均50.1点　英語…平均54.6点
公立高校入試解説ページに戻る

◆menu◆ 公立高校入試…数学は全国。千葉だけ５教科あります。％は正答率。
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ。ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記
ＱＵＩＺ…☆４以上はムズいよ！
サボのツイッターはコチラ→