平均24.1点(50点満点、前年比;+5.4点)
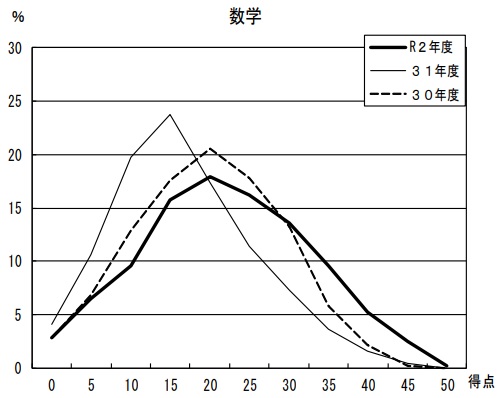
問題はこちら→リセマムさん
大問1(小問集合)
(1)
5-2×(-3)
=5+6
=11
(2)
(2a+5)/3-a/2
={2(2a+5)-3a}/6
=(a+10)/6
(3)
√45+2√5-√125
=3√5+2√5-5√5
=0
(4)
文字式が表す内容を言葉で説明する。
みかん5個(5a円)とりんご3個(3b円)の合計の金額は1000円以下である。
(5)
a2+8a-20
=(a+10)(a-2)
(6)
3x2-5x+1=0
解の公式を適用。
x=(5±√13)/6
(7)
反比例は積xyが比例定数aで一定。
a=3×(-4)=-12
y=-12/x
y=-12÷(-2)=6
(8)①
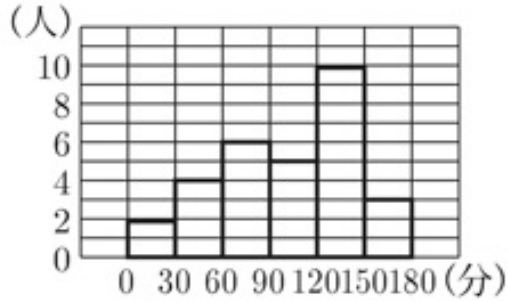
見えない部分は、30-(2+4+5+10+3)=6
最頻値(モード)は最もあらわれている値。
120~150の階級で、この階級値は120と150の平均である135分。
エ
(9)①
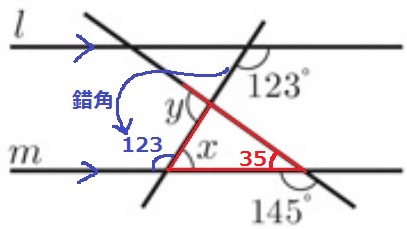
錯角で123°をおろす。
x=180-123=57°
②
赤線で外角定理。
y=35+57=92°
(10)①
1:1:√2の直角三角形。
AC=2×√2=2√2cm
②
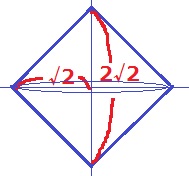
2つの円錐が上下でくっついている図形になる。
底面は半径√2cmの円、高さの合計は2√2cm
√2×√2×π×2√2÷3=4√2/3πcm3
大問2(小問集合2)
(1)①
A…1000/15000=1/15=1.33…/20
B…1000/20000=1/20
C…1500/20000=1.5/20
サボは最初に0を3つ消しました。Cの分子は1.5になる。
Aの分母を15から20に変える。分子は、1×20/15=4/3=1.33…
分子の大きい順にC→A→B
②【1】
同数の目が出るのは1~6の6通り。
6/36=1/6
【2】
10a+bは2桁の整数。
2桁の9の倍数を並べると、〔18・27・36・45・56・63・72…〕
このうち1~6の数字が使われるのは4つだけ。
4/36=1/9
(2)①
y=ax2に(x、y)=(-1、5)を代入。
5=(-1)2a
a=5
y=5x2
②
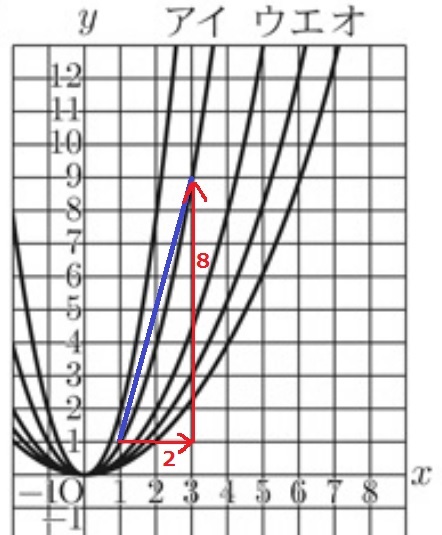
xが-3から-1まで増加するとyが8減少した。
y=ax2のグラフはy軸に対称なので、
xが1から3まで増加するとyが8増加することになる。
イ
③
yの変域が0以下なので、グラフは上に凸となる。
x=0のとき、最大値y=0
x=3のとき、最小値y=-3
y=ax2は(3、-3)を通る。
-3=32a
a=-1/3
y=-1/3x2
大問3(方程式)
(1)
団体割引がきくので、1人あたりの入場料は300×80%=240円
(2)①
イが先に求まる。
イ=30-24=6
ア=6-1=5
ア…5、イ…6
②【1】
それぞれの料金にそれぞれの人数をかけて足す。
両方に乗らなかった1人は0円だから不要。
600x+400y+300×5=14700
【2】
人数…x+y=24 …①
料金…600x+400y=13200 …③
③÷200
3x+2y=66 …④
④-①×2
3x+2y=66
-)2x+2y=48
x =18
①より、y=24-18=6
x=18 y=6
(3)①
1つは無料でついてくるので5個買う。
150×5=750円
②
5の倍数個(5n個)のときに、1人あたりの金額が120円となる説明。
5の倍数以外のnは考えない。
5n個買うと無料でついてくる個数は、5n÷5=n個
実際に支払うのは150円×4個のnセット分なので150×4n円。
これを実際にもらう5n個でわると、1個あたりの代金は120円となる。
(150×4n)/5n=120
ウ…n、エ…(150×4n)/5n=120
*5個もらうには4個買えばいいので、4×150=600円
これを÷5して1個あたりの値段は、600÷5=120円
5個をn倍した5n個も同じ。
大問4(平面図形)
(1)
3点が円周上にくる円の中心の作図。
AB、BC、CAから2本の垂直二等分線をつくり、交点がO。
(2)①
△ABE∽△CDEの証明。

対頂角と円周角の定理から2角が等しく∽
②
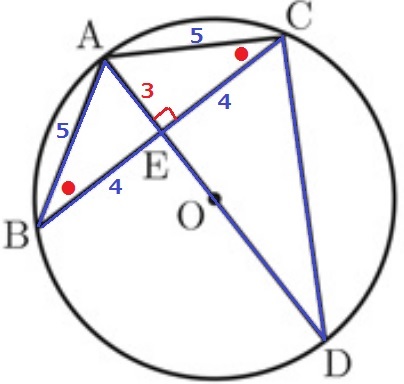
AB=ACより、△ABCは二等辺三角形。
EはBCの中点。二等辺の頂角を通る垂線は底辺を二等分する。
BE=EC=4cm
△ABEで三平方→3:4:5の直角三角形でAE=3cm
ここで①の△ABE∽△CDEより、△CDEの辺の比も3:4:5
CD=4×5/3=20/3cm
③
△CDEの3:4:5から、ED=4×4/3=16/3cm
直径AD=3+16/3=25/3cm
半径は、25/3÷2=25/6cm
④
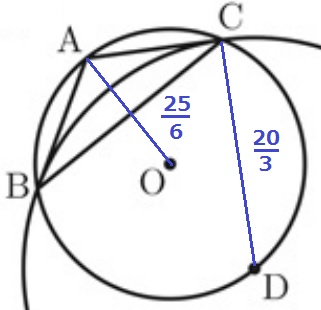
特殊な問題だが、すでに必要な情報はそろっている。
③より、円Oの半径は25/6cm
②より、円Dの半径CDは20/3cm
円Oの半径:円Dの半径
=25/6:20/3=5:8
円の面積比は半径の2乗。
円Oと円Dの面積比は25:64
大問5(数量変化)
(1)
表から130分後に道の駅に着いた。
9時の130分後は11時10分。
(2)
途中、30分間公園で休んでいる。
130-30=100分後
(3)①
こうたは10分間で5km移動する。
5÷10=分速0.5km
*単位はkmに注意!
②
こうたのグラフは(50、0)(60、5)を通過する。
変化の割合a=yの増加量÷xの増加量
=(5-0)/(60-50)=1/2
y=1/2x+bに(0、50)を代入。
0=1/2×50+b
b=-25
y=1/2x-25
③
公園で合流するので、先ほどの式にy=12を代入。
12=1/2x-25
x=74
9時の74分後である10時14分。
(4)
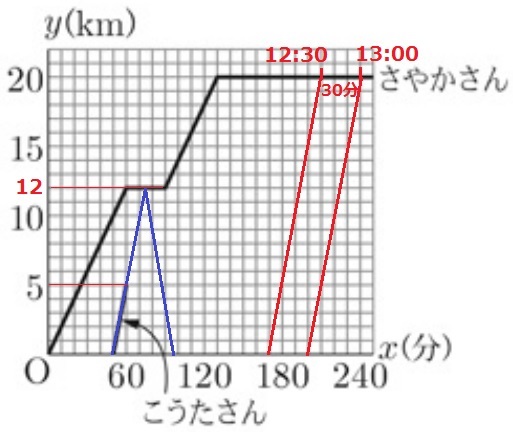
こうたは道の駅まで、20km÷分速0.5km=40分かかる。
13:00-40=12:20までに出発する。
その30分前の11:50分から出発すればいい。
11時50分から12時20分
●講評●
大問1
すべて基本なのですべてとろう。
大問2
(1)①
約分して比較する。
(2)②y=ax2の傾きは変化する。本問は対称性を利用。
大問3
(1)30人全員ではなく、1人あたりの入場料を求める。
(3)②仕組みは4人分の料金÷5人。それにnをくっつけただけ。
条件の特殊性があまり活かされていないように思えるのだが。
大問4
(2)①相似の証明も易。
後半戦も直角三角形さえ見つければ3:4:5で全部いける。
(4)前問が誘導になっている。特殊な感じだが難しくはなかった。
大問5
不可解な点が多い。
(3)②のグラフの式以外はすべて算数で終わらせることができる。
(4)あまり良い問題ではなかった。以下、公式の検査結果より。


大問4(2)③正答率9.6%
大問5(3)③正答率18.8%



コメント