2021年度　神奈川県公立高校入試・追検査【数学】解説

問題はコチラ→ＰＤＦファイル
本試験（数学）の解説はコチラ→2021年度神奈川

大問１（計算）

（ア）
５－（－８）
＝５＋８＝13　【４】

（イ）
－１/３＋３/５
＝４/15　【３】

（ウ）
（２ｘ－ｙ）/３－（ｘ＋２ｙ）/２
＝｛２（２ｘ－ｙ）－３（ｘ＋２ｙ）｝/６
＝（ｘ－８ｙ）/６　【１】

（エ）
21/√３－√75
＝７√３－５√３＝２√３　【２】

（オ）
（ｘ＋４）（ｘ－７）－（ｘ＋２）²
＝ｘ²－３ｘ－28－ｘ²－４ｘ－４
＝－７ｘ－32　【１】

大問２（小問集合）

（ア）
ｘ＝１、ｙ＝－３を代入する。
ａ－３ｂ＝６
３ａ＋ｂ＝８
うえの連立を解くとａ＝３、ｂ＝－１　【３】

（イ）
３ｘ²－７ｘ－１＝０
解の公式を適用。
ｘ＝（７±√61）/６　【４】

（ウ）
ｙ＝－３ｘにおいて、変化の割合は傾きであるー３。
ｙ＝ａｘ²において、ｘの値が２→４に増加するときの変化の割合は、
ａ（２＋４）＝６ａ
６ａ＝－３
ａ＝－１/２　【１】

（エ）

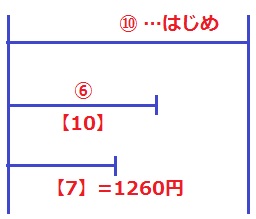
線分図で表す。
最初に⑩持っていた。④使って残りは⑥。
これを【10】としたときに【３】使い、余った【７】が1260円。
はじめの所持金は、1260×【10】/【７】×⑩/⑥＝3000円　【２】

（オ）
468＝２²×３²×13
平方数をかけると根号が外れる。各素因数を偶数個にすればいい。
最も小さいｎは、13×１×１＝13
２番目に小さいｎは、13×２×２＝52
３番目に小さいｎは、13×３×３＝117　【４】

（カ）
ポイントはＤＥが中心Ｏを通過すること。

ＤＥを延長、円との交点をＦとする。
半円の弧に対する円周角より、∠ＤＡＦ＝90°
∠ＣＡＦ＝90－36＝54°
弧ＣＦに対する円周角と錯角で移動して、∠ＤＥＡ＝54°
∠ＢＥＤ＝180－54＝126°　【３】

大問３（小問集合２）

（ア）ⅰ
△ＡＦＤ≡△ＣＧＢの証明。

平行四辺形の対辺でＡＤ＝ＣＢ
ＡＤ//ＢＣで錯角→∠ＡＤＦ＝∠ＣＢＧ

∠ＡＦＤの対頂角→∠ＢＦＥ＝●
さらに、ＥＡ//ＣＧの同位角で∠ＢＦＥ＝∠ＢＧＣ（●）
△ＡＦＤと△ＣＧＢの残りの内角が等しく、∠ＤＡＦ＝∠ＢＣＧ（△）
以上、１辺と両端角が等しく合同。
ａ…【３】、ｂ…【１】

ⅱ
挑むには覚悟が求められる(´～`)

60°は平行四辺形の高さ用に与えられているので、１：２：√３から高さは３√３/２ｃｍ。
平行四辺形ＡＢＣＤの面積は、４×３√３/２＝６√３ｃｍ²
ＦＥ//ＧＣより、△ＤＦＥ∽△ＤＧＣでＤＦ：ＦＧ＝ＤＥ：ＥＣ＝②：①
前問の合同から対応する辺が等しく、ＢＧ＝ＤＦ＝②
△ＢＣＪ∽△ＤＨＪに注目して、ＢＪ：ＪＤ＝４：１
連比処理にかけるとＢＤ＝⑤なので〇の比と等しい！
ＦＪ＝ＦＤ－ＪＤ＝②－①＝①

ＦＩ//ＧＣで△ＪＦＩ∽△ＪＧＣ→ＪＩ：ＩＣ＝ＪＦ：ＦＧ＝①：①
あとは、△ＣＥＩと△ＣＤＪで隣辺比に持っていくのが良いと思います。
△ＣＥＩ…１×１＝【１】
△ＣＤＪ…３×２＝【６】
四角形ＤＪＩＥ…【６】－【１】＝【５】
〔平行四辺形ＡＢＣＤ⇒△ＢＣＤ⇒△ＣＤＪ⇒四角形ＤＪＩＥ〕
６√３×１/２×①/⑤×【５】/【６】＝√３/２ｃｍ²

（イ）
あ：20人の中央値（メジアン）は10番目と11番目の平均→４～６本
25人の中央値は13番目→６～８本。２年生の方が大きい。×
い：１年生…５/20、２年生…５/25
分子が同じだから、分母の大きい２年生の方が割合は小さい。〇
う：最頻値（モード）は最もあらわれている値。４～６本の階級値は５本。〇
え：範囲（レンジ）＝最大値－最小値
14本未満（14を含まない）ので、範囲は14本ではない。×
い、う

（ウ）

長方形はやりやすい。グラフの頂上の横（時間）が半分で、高さ（面積）も半分になる。
大問題は台形…。
ＡＢ＝15ｃｍだから頂上に着くまでの時間は半分になるが、４～６がすべて一緒…。
とどのつまり、△ＡＰＤの面積を出すしかない。
台形ＡＢＣＤは等脚台形で、外側に直角三角形をつくると辺の比が３：４：５。
→台形の高さは12ｃｍ、ＡＤ＝45－９×２＝27ｃｍ
△ＡＰＤの最大値は27×12÷２＝162となる。
ⅰ…【２】、ⅱ…【６】

（エ）ⅰ
またもや意地悪な設問(ﾉ)`ω´(ヾ)
りんごの個数をｘ個とおく。
３個ずつ袋に入れたらちょうどだったなので、右辺のｘ/３は袋の数を示す。
つまり、袋の数で等式を立てている。
袋に５個ずつ入れると、りんご４個と８袋が余った。
袋に入れたリンゴはｘ－４個、リンゴが入った袋の数は（ｘ－４）/５袋。
これに８袋足して、袋の合計は（ｘ－４）/５＋８

ⅱ
（ｘ－４）/５＋８＝ｘ/３
３ｘ－12＋120＝５ｘ
２ｘ＝108
ｘ＝54
りんごは54個。

＠余談＠
袋の数をｘ個としてリンゴの個数で等式を立てると、
５（ｘ－８）＋４＝３ｘ
ｘ＝18
リンゴの数は、３×18＝54個

大問４（関数）

（ア）
ｙ＝ｘより、Ａ（３、３）
これをｙ＝ａｘ²に代入。
３＝３²ａ
ａ＝１/３　【３】

（イ）

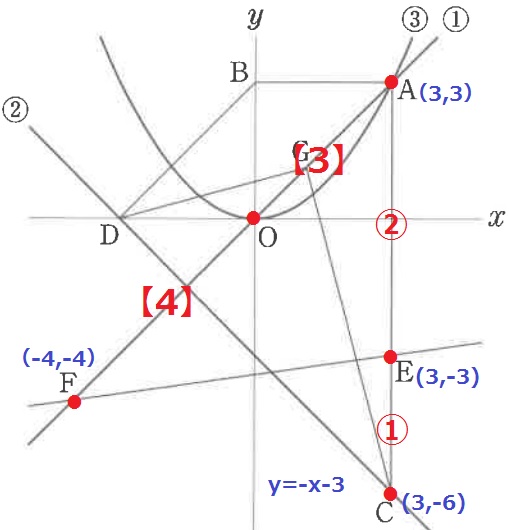
↑座標を確定するとこうなります。
Ｆ（－４、－４）⇒Ｅ（３、－３）
右に７、上に１だから、傾きｍ＝１/７

ｙ＝１/７ｘ＋ｎに（３、－３）を代入。
－３＝１/７×３＋ｎ
ｎ＝－24/７
ⅰ…【２】、ⅱ…【４】

（ウ）
キビシイ:(っ`ω´c):
四角形ＡＢＤＣの面積の半分が△ＣＧＤになる。

パッと見て、ＢＤとＡＦが平行っぽい。
ＢＤの傾きを調べると45度線で、ＡＦの傾き１と同じで平行。
ＡＦとＤＣの交点とＨとおく。
Ｈはｙ＝ｘとｙ＝－ｘ－３の交点なので、
ｘ＝－ｘ－３
ｘ＝－1.5
Ｈ（－1.5、－1.5）

四角形ＡＢＤＨは台形で上底ＢＤと下底ＡＨの比は、
ｘ座標の差から、ＢＤ：ＡＨ＝３：4.5＝②：③

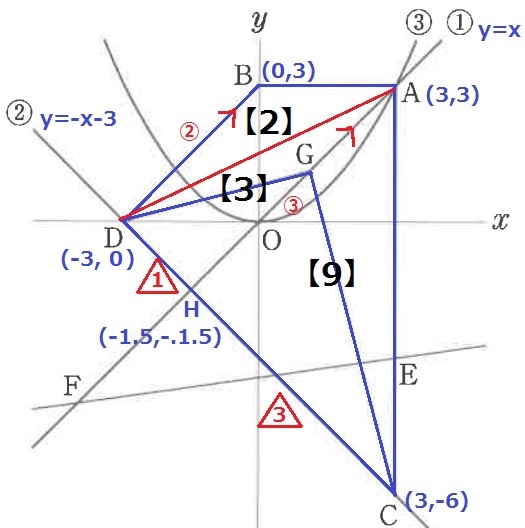
ＡＤに補助線。
上底と下底の比から△ＡＢＤの面積を【２】とすると、△ＡＤＨは【３】
△ＡＤＨ：△ＡＨＣ＝ＤＨ：ＨＣ＝1.5：4.5＝△１：△３
△ＡＨＣの面積は、【３】×３＝【９】
四角形ＡＢＤＣの面積は【14】なので、△ＣＧＤを【７】にすればいい。

↑つまり、こう！
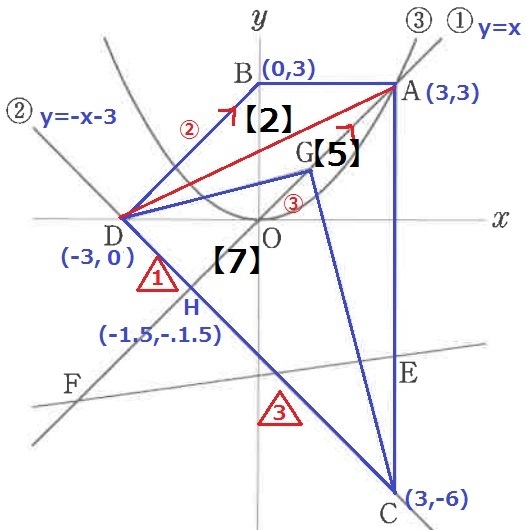
ＨＧ：ＧＡ＝△ＣＧＤ：四角形ＣＡＤＧ＝７：５
Ｇのｘ座標は、－1.5＋｛３－（－1.5）｝×【７】/【12】＝９/８

大問５（確率）

（ア）
和が12以上→５＋７、６＋７しかない。
初期状態で右端にある７は操作１で必ず移動する。
操作１で７を５か６とチェンジ（２通り）
操作２で７を必ずチェンジさせる。
よって、２通りしかない。
確率は２/36＝１/18　【２】

（イ）
地道にやっていくしかない(´･ω･`)
◆操作１で１
〔7234561〕→１を出して１と７をチェンジ（１通り）
◆操作１で２
〔1734562〕→左端にある１は操作２で必ず移動するから、
２より大きいものが左端にくるので無理。
◆操作１で３
〔1274563〕→６を出して２と１をチェンジ（１通り）
◆操作１で４
〔1237564〕→５か６を出す（２通り）
◆操作１で５
〔1234765〕→４・５・６を出す（３通り）
◆操作１で６
〔1234576〕→３・４・５・６を出す（４通り）
計11通りで、確率は11/36

大問６（空間図形）

（ア）

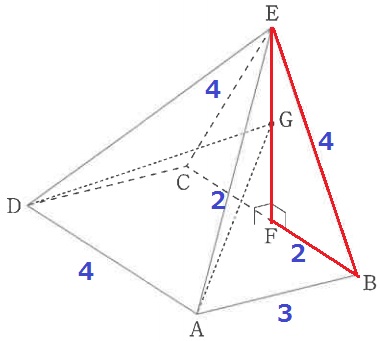
四角錘の高さはＥＦにあたる。
△ＥＦＢで三平方→ＥＦ＝２√３ｃｍ
四角錘の体積は、４×３×２√３÷３＝８√３ｃｍ³　【３】

（イ）

△ＡＢＦで三平方→ＡＦ＝√13ｃｍ
ＧＦ＝２√３÷２＝√３ｃｍ
△ＡＦＧで三平方→ＧＡ＝４ｃｍ
対称性から、ＧＤ＝４ｃｍ

△ＧＤＡは１辺４ｃｍの正三角形で、△ＥＣＢと合同。
△ＥＣＢを求積すればいい。４×２√３÷２＝４√３ｃｍ²　【４】

（ウ）

展開図を作成。
ＤＡとＥＢ、ＥＣとの交点をそれぞれＨ、Ｉとする。
対称図形なので、ＤＡ//ＣＢ

錯角で∠ＤＩＣ＝∠ＢＣＩ＝60°
△ＩＤＣの内角は30°－60°－90°で辺の比は１：２：√３。
ＩＣ＝３×１/√３＝√３ｃｍ
ＤＩ＝√３×２＝２√３ｃｍ
対称性から、ＡＨ＝ＤＩ＝２√３ｃｍ

△ＥＢＣは１辺４ｃｍの正三角形→ＥＩ＝４－√３ｃｍ
また、△ＥＩＨも正三角形だから、ＩＨ＝４－√３ｃｍ
ＤＡ＝２√３×２＋（４－√３）＝４＋３√３ｃｍ

＠2021年度・神奈川解説＠
数学…平均58.2点　社会…平均72.6点　理科…平均50.1点　英語…平均54.6点
公立高校入試解説ページに戻る