2021年度　京都府公立高校入試問題過去問・前期【数学】解説

問題はコチラ→ＰＤＦファイル
出題範囲の除外は三平方の定理と標本調査。
2021年度・京都中期の解説はコチラから。

大問１（小問集合）

（１）
（－２）²－（－６²）×２/３
＝４－（－36）×２/３
＝４＋24
＝28

（２）
ｘ－２ｙ－（ｘ－９ｙ）/５
＝（５ｘ－10ｙ－ｘ＋９ｙ）/５
＝（４ｘ－ｙ）/５

（３）
（ａ＋５）（ａ－３）－（ａ＋４）（ａ－４）
＝ａ²＋２ａー15－ａ²＋16
＝２ａ＋１

（４）
反比例の比例定数ａは積ｘｙで一定。
ｙ＝－９×８/３÷４＝－６

（５）
２ｘ＋３ｙ－５＝４ｘ＋５ｙ－21＝10
２ｘ＋３ｙ－５＝10
２ｘ＋３ｙ＝15　…①
４ｘ＋５ｙ－21＝10
４ｘ＋５ｙ＝31　…②

①×２－②
４ｘ＋６ｙ＝30
－)４ｘ＋５ｙ＝31
ｙ＝－１
①に代入。２ｘ－３＝15
ｘ＝９
ｘ＝９、ｙ＝－１

（６）
外角の大きさを①とおくと、内角の大きさは⑨。
外角…180×①/⑩＝18°
多角形の外角の和は360°だから、正多角形の外角の数は360÷18＝20個
外角の数＝頂点の数＝辺の本数で20本。

（７）
√９＜√10＜√16より、３＜√10＜４
絶対値は数直線上で原点０からの距離。
－４より大きく、４より小さい整数を答える。整数は負の数と０を含む。
－３・－２・－１・０・１・２・３の７個。

（８）
ｘ²－８ｘ－７＝０
解の公式。ｘの係数が偶数なのでｂ＝２ｂ’が使える。
ｘ＝４±√23

（９）
推論が絡むデータの活用問題。
昇順に並べると、〔11・12・14・15・21〕
３番目の中央値が14から15に変わるから、
11～14のいずれかが誤りで、正しい記録ｎは15以上。

総和＝平均×個数＝15×５＝75本
訂正前の総和は、11＋12＋14＋15＋21＝73本
訂正後で２本多くなる。
２本増やして15以上となるのは、火曜日の14本。
イ、ｎ＝14＋２＝16

大問２（確率）

（１）
全体は５×４＝20通り
残った３枚の最小値が３ということは、１と２を抜き取る。
（１、２）（２、１）の２通り。
確率は、２/20＝１/10

（２）
素数はバラバラなので書き出しです。
１～５の数で重複しない２桁の素数は〔13・23・31・41・43・53〕
【13】
１を取り出す。（ａ＝１）
ｂは残った３枚の最小値。２を取り出せば最小値は３になる。１通り
【23】
２を取り出す。１を取り出せば最小値は３になる。１通り
【31】
３を取り出す。２・４・５を取り出せば１が最小値。３通り
【41】
４を取り出す。２・３・５を取り出せば１が最小値。３通り
【43】
４を取り出す。１・２が残っているので１回の取り出しで３を最小値にできない。×
【53】
５を取り出す。１・２が残っているので１回の取り出しで３を最小値にできない。×
計８通り。
確率は、８/20＝２/５

大問３（数量変化）

（１）

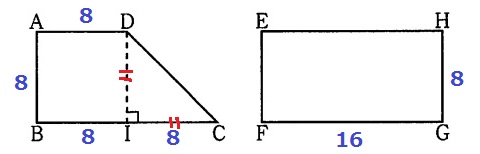
長さを図に書き込もう。
△ＣＤＩは直角二等辺だから、ＩＣ＝８ｃｍ
台形ＡＢＣＤと長方形ＥＦＧＨの底辺は16ｃｍ。

ｘ＝３のとき、ｙ＝６×６÷２＝18
ｘ＝５のとき、ｙ＝（２＋10）×８÷２＝48

（２）
よくある移動なので即答したい。
①０≦ｘ≦４のとき、重なる部分は直角二等辺三角形。
底辺と高さがともに伸びるのでｙはｘの２乗に比例する。エ

②４≦ｘ≦８のとき、重なる部分は台形。
上底と下底の和は伸びるが高さは一定。（グラフは直線）
原点からｙ＝ａｘ²で始まり、ｘ＝４から一次関数に変わる。
原点を通らない（比例ではない）一次関数。ウ

（３）
出題の仕方がやや変わっている。
ｘ＝２のとき、ｙ＝４×４÷２＝８
ｘ＝３のとき、ｙ＝６×６÷２＝18
ｙの増加量は18－８＝10
ｘ＝３のときのｙ＝18に10×６＝60を加え、ｙ＝78のときのｘを求めればいい。

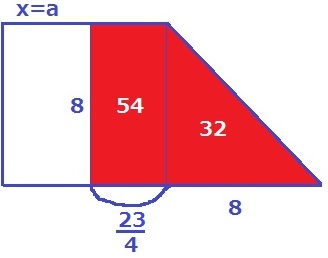
４秒後の直角二等辺が８×８÷２＝32なので、左の長方形は78－32＝46
この底辺の長さは46÷８＝23/４ｃｍ
秒速２ｃｍで移動するから、ａ＝４＋23/４÷２＝55/８

大問４（平面図形）

（１）
四角形ＡＥＣＦが平行四辺形である証明。

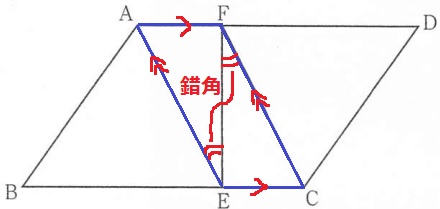
平行四辺形であるための５つの条件のうち、
定義である２組の対辺が平行である点を指摘すればＯＫ。
仮定より、ＡＦ//ＥＣ
∠ＡＥＦ＝∠ＣＦＥ→錯角が等しい→ＡＥ//ＦＣ

（２）

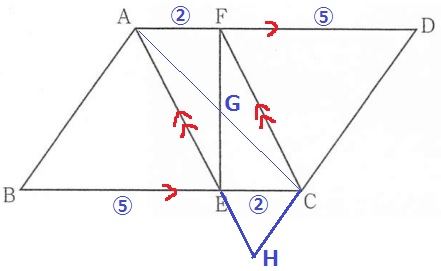
ＢＥ＝⑤、ＥＣ＝②
平行四辺形ＡＥＣＦの対辺は等しい→ＡＦ＝②
ＦＤ＝⑤

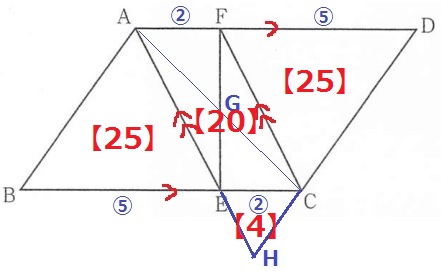
△ＥＣＨ∽△ＡＤＨ∽△ＦＤＣ
面積比は相似比の２乗。
△ＥＣＨ＝②×②＝【４】
△ＦＤＣ＝⑤×⑤＝【25】
△ＡＤＨ＝⑦×⑦＝【49】
平行四辺形ＡＥＣＦ＝【49】－【25】－【４】＝【20】
△ＥＢＡは底辺が⑤→対称性から△ＦＤＣと合同【25】
平行四辺形ＡＢＣＤの面積は【70】

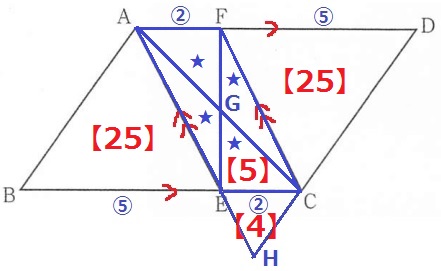
△ＧＥＣは平行四辺形ＡＥＣＦの対角線ＡＣとＥＦで４等分された三角形の１つ。
△ＧＥＣ＝【20】÷４＝【５】
四角形ＣＧＥＨ＝【５】＋【４】＝【９】
四角形ＣＧＥＨ：平行四辺形ＡＢＣＤ＝９：70

大問５（空間図形）

（１）
円Ｏの周の長さは12πｃｍ。
円Ｏの直径は、12π÷π＝12ｃｍ
円Ｏの半径は、12÷２＝６ｃｍ

【球の体積Ｖ＝４/３πｒ³】
半球なので、÷２を忘れずに。
水の体積は、４/３π×６³÷２＝144πｃｍ³

（２）

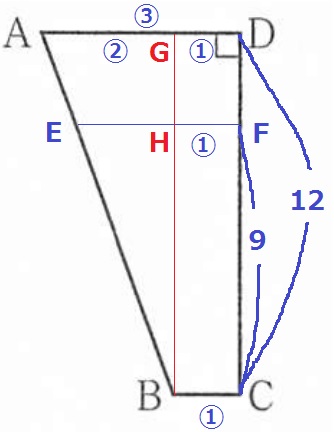
台形ＡＢＣＤにＥ、Ｆを図示。
ＢからＡＤに向けて垂線。ＡＤ、ＥＦとの交点をＧ、Ｈとする。
△ＡＢＧ∽△ＥＢＨより、ＥＨ＝②×９/12＝〇1.5
ＥＦ＝〇1.5＋①＝〇2.5
ＡＤ：ＥＦ＝③：〇2.5＝６：５

（３）

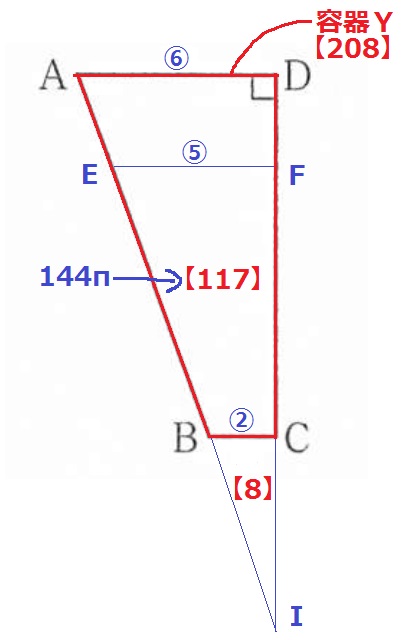
比を統一すると、ＡＤ：ＥＦ：ＢＣ＝⑥：⑤：②
ＡＢとＤＣを延長して交点をＩとする。
△ＢＩＣ∽△ＥＩＦ∽△ＡＩＤ
体積比は相似比の３乗。
水で満たされている台形ＥＢＣＦの部分は、
⑤×⑤×⑤－②×②×②＝【117】＝容器Ｘの144πｃｍ³
容器Ｙは台形ＡＢＣＤの部分で、⑥×⑥×⑥－②×②×②＝【208】
容器Ｙの体積は、144×208/117＝256πｃｍ³

大問６（規則）

（１）

左から２番目は３ずつ増えている。
13

（２）

２Ａ＋Ｂ＝32　…①
Ａ＋２Ｂ＝－８　…②

①×２－②で、３Ａ＝72
Ａ＝24
①に代入。Ｂ＝－16
Ａ…24、Ｂ…－16

（３）

『ｍ段目の左からｍ番目』
１段目の左から１番目、２段目の左から２番目をみると…
【22、20、18、16…】
初項が22で、２ずつ減っている。
22－２（ｍ－１）
＝24－２ｍ

『ｍ段目の左から２番目』
【－２、20、42、64…】
初項が－２で、22ずつ増えている。
－２＋22（ｍ－１）＝22ｍ－24
２ｍ段目なので、22×２ｍ－24＝44ｍ－24

44ｍ－24＝（24－２ｍ）²
44ｍ－24＝576－96ｍ＋４ｍ²
４ｍ²－140ｍ＋600＝０　←÷４
ｍ²－35ｍ＋150
＝（ｍ－５）（ｍ－30）＝０
ｍ＝５、30