2019年度　神奈川県公立高校過去問【数学】解説

平均50.3点

問題はコチラ→ＰＤＦファイル
2019年度・神奈川数学(鬼畜追検査)はコチラ。
ゲロムズなのだが。

大問１（計算）

（ア）　98.1％
（－７）＋（－１３）
＝－７－１３＝－２０　【１】

（イ）　98.3％
－３/５＋３/７＝－６/３５　【２】

（ウ）　98.8％
32ａｂ²÷（－４ｂ）＝－８ａｂ　【３】

（エ）　98.2％
√63＋42/√７＝３√７＋６√７＝９√７　【２】

（オ）　95.2％
（ｘ＋４）²－（ｘ－５）（ｘ－４）
＝ｘ²＋８ｘ＋１６－（ｘ²－９ｘ＋２０）
＝１７ｘ－４　【４】

大問２（計算２）

（ア）　94.3％
（ｘ－４）²＋８（ｘ－４）－３３　←（ｘ－４）をラージエックスに置き換え
＝Ｘ²＋８Ｘ－３３
＝（Ｘ＋１１）（Ｘ－３）
＝{（ｘ－４）＋１１}{（ｘ－４）－３}　←ラージエックスを戻す
＝（ｘ＋７）（ｘ－７）　【１】

（イ）　88.6％
３ｘ²－８ｘ＋２＝０
解の公式（ｂ＝2ｂ’ver）
ａ＝{４±√（４²－３・２）}/３
＝（４±√１０）/３　【２】

（ウ）　78.8％
傾きが負なので、上に凸のグラフ。
最大値はｘ＝０、ｙ＝０（ｂ）･･･原点
最小値はｘ＝－３、ｙ＝ａ
ａ＝－２/３×（－３）^２＝－６
ａ＝－６、ｂ＝０　【１】

（エ）　79.9％
代金の合計が２ａ＋ｂ。
３割引き→定価の７割　【４】

（オ）　89.0％
根号の大小関係は、２乗して根号を外す。
（５√３）²＝７５、
８²＝６４、（√７９）²＝７９。
よって、８＜５√３＜√７９　【３】

（カ）　95.0％
標本調査。
全体：不良品＝500：６だから、
30000×６/500＝３６０個　　【３】

ここまでで３７点。
後ろに難問が揃っているので、確実にとりたい。

大問３（小問集合）

（ア）　40.3％
円がでてきたら、真っ先に半径の作図と円周角の定理を疑う。

△ＯＢＣが半径で二等辺。∠ＢＯＣ＝８８°
円周角で∠ＢＡＣ＝４４°
△ＡＢＣも二等辺だから、∠ＡＢＣ＝６８°で、∠ＡＢＤ＝２２°
外角定理で、∠ＢＤＣ＝２２＋４４＝６６°

（イ）　2.1％!!
もはや小問ではない(llﾟдﾟll)
まず、ＤＣ上の辺の比から調べる。

メネラウスの定理で、ＡＢ/ＢＤ×ＤＧ/ＧＣ×ＣＥ/ＥＡ＝１
２/１×ＤＧ/ＧＣ×２/１＝１　→ＤＧ：ＧＣ＝１：４

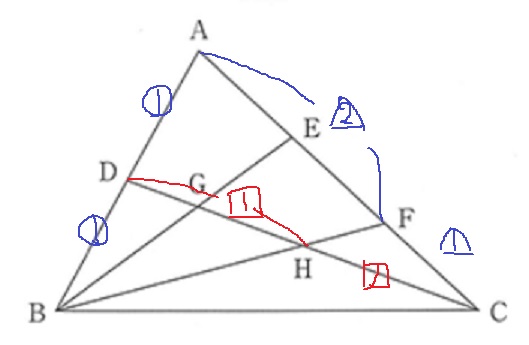
同じくメネラウス。ＡＢ/ＢＤ×ＤＨ/ＨＣ×ＣＦ/ＦＡ＝１
２/１×ＤＨ/ＨＣ×１/２＝１　→ＤＨ：ＨＣ＝１：１
ＨはＤＣの中点になる。図２ではＣよりに見えるが･･･。
２つの比を組み合わせると、
ＤＧ：ＧＨ：ＨＣ＝２：３：５

△ＢＧＤは△ＡＢＣの何分の何か。

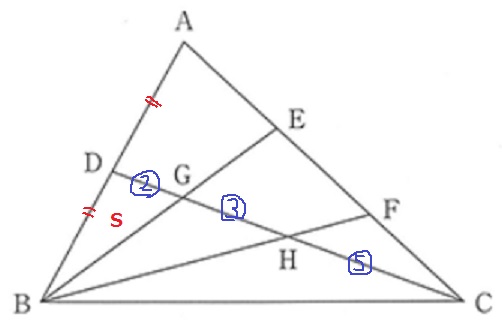
１×１/２×２/１０＝１/１０
大問題はＴ(llﾟдﾟll)

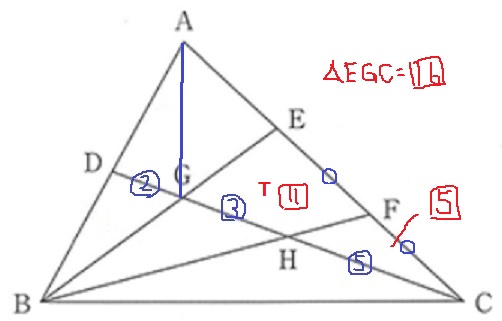
△ＣＥＧ内で面積比の計算。
△ＣＦＨは、⑤×１＝□５
△ＣＥＧは、⑧×２＝□１６
残りの四角形ＥＧＨＦは□１１。
よって、四角形ＥＧＨＦは△ＡＢＣの･･･
１×１/２×８/１０×２/３×１１/１６＝１１/６０

したがって、△ＢＧＤ（Ｓ）：四角形ＥＧＨＦ（Ｔ）
＝１/１０：１１/６０＝６：１１
他にスマートなやり方あるかな(;￣Д￣)

（ウ）　6.8％!!
子どもではなく、みかんの数がｘに指定されている。
i；（ｘ＋８）/６＝（ｘ－５）/５
プラスマイナスに気を付けよう。
不足分は足し、余りは引き、帳尻を合わせたあとに割る。
ii；上の式を解いて７０個

大問４（関数）

（ア）　84.2％
Ｃ（－３、－２）がわかっているので、
これをｙ＝ａｘ²に当てはめ。
－２＝３ａ²
９ａ＝－２
ａ＝－２/９　【５】

（イ）ｉ　29.7％！
ＡＤ：ＤＣ＝２：１から、ＡＤとＤＣの長さを求める。
ＡＤ＝１０/３、ＤＣ＝５/３

ＡＤ＝ＥＦなので、ＥＦ＝１０/３
ここで四角形ＡＤＥＦに注目。
ＡＤとＦＥ（対辺）が平行で、長さが等しい。
よって、四角形ＡＤＥＦは平行四辺形。
ＡＦ//ＤＢ（ＤＥ）
ＤＢの傾きは、Ｄ（－３、－１/３）とＢ（３、３）から求める。
ｙの増加量/ｘの増加量＝{３－（－１/３）｝/｛３－(－３)}/＝５/９。
ＡＦの傾きも５/９。
ＡとＢはｙ軸を対称の軸とした対称関係にあるので、
ＡＦとＢＦも同様に対称関係にある。
ＡＦの傾きが５/９だから、ＢＦの傾きは－５/９となる。　【２】

ｉｉ
前問からＢＦの傾きは－５/９。これをＢ（３、３）に放り込む。
３＝－５/９×３＋ｂ
ｂ＝１４/３　【４】

（ウ）　2.0％!!!
面積が等しいとなれば等積変形が頭をよぎるが、
求めるのはＧの座標なので、点を移動するとうまくいかないような気がする…。
とりあえず、求められるところを洗い出す。

座標をもとに計算すると、四角形ＡＤＢＦの面積が先に求まる。
△ＢＤＧは１５ｃｍ²になる。
このあとで手詰まる人が多かったと思われる。

求めるＧのｘ座標をｓとおいて、Ｇ（ｓ、－ｓ）
長方形を描き、長方形の面積から等式の作成を試みる。

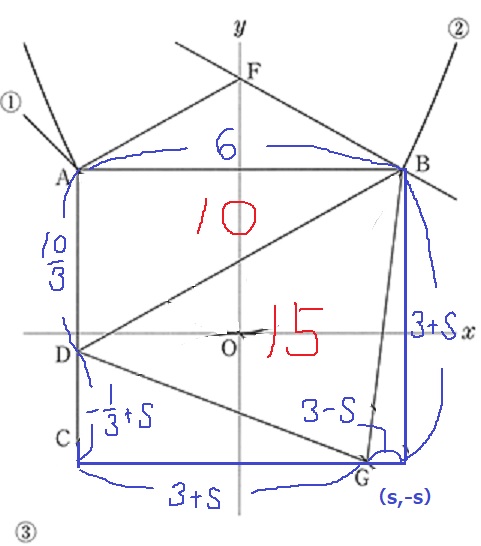
↑邪魔な線を消してます。ここまで整理するのに時間かかるよ！
【長方形の面積＝中にある４つの三角形の面積】
ｓがでる２つの三角形は、１辺の長さが（３＋ｓ）で等しい。
６（３＋ｓ）＝（－１/３＋ｓ＋３－ｓ）×（３＋ｓ）×１/２＋１０＋１５
１８＋６ｓ＝８/３×（３＋ｓ）×１/２＋２５
１４/３ｓ＝１１
ｘ＝３３/１４
あれこれ練ったんですけど、これしか思い浮かばなかった…。
グラフが複雑で、辺の長さを調査するにも時間がかかるので、ここだけでもヘビー。

＠別解＠
ＹＡさん（@r21h238ya）から素晴らしい解法を頂きました。
～～～
四角形ＡＤＢＦと△ＤＧＢが等しくなるようにＧを求める。
①とＤＢの交点をＰとすると、
－ｘ＝９/５ｘ＋４/３
Ｐ（－６/７,６/７）

ＡからＤＢに垂線でＲ、ＧからＤＢに垂線でＲとすると、
△ＡＱＰ∽△ＧＲＰが得られる。

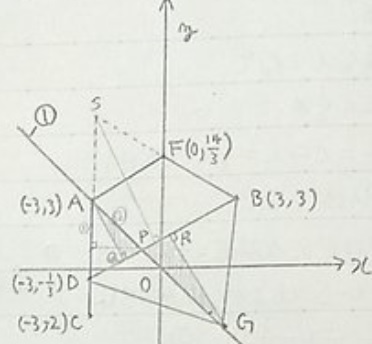
ＡＰの長さを求める。
ＡとＰのｘ座標の距離は３－６/７＝15/７
①は45°の傾きなので、１：√２より、ＡＰ＝15√２/７

面積が等しくなるときの高さの比を求める。
ＡＦ：ＤＢ＝１：２、ＡＦ//ＤＢなので、
ＤＡの延長線とＢＦの延長線の交点をＤとすると、
△ＳＤＢ∽△ＳＡＦとなり、面積比は４：１である。
つまり、２ＡＱ（△ＳＤＢの高さ）×３/４＝３/２ＡＱの長さがＧＲになればよい。

ＡＱ：ＧＲ＝２：３となるので、ＡＰ：ＧＰ＝２：３

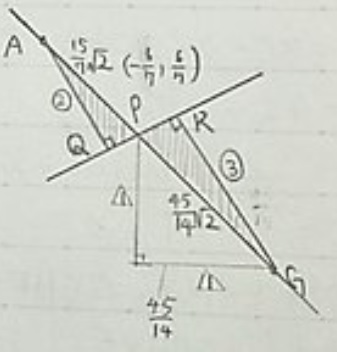
ＧＰ＝15√２/７×３/２＝45√２/14
１：√２を利用して、Ｇのｘ座標はＰのｘ座標に＋45/14をする。
－６/７＋45/14＝33/14
～～～
三角形ＢＤＧと四角形ＡＤＢＦはＤＢを共通辺とするので、
ＤＢを底辺とおいたときの高さを考えます。
①の傾きが45°なので、座標の距離を√２倍すれば出ますね。
ＡＤＢＦは台形なので、ちょいと工夫する必要があり、上の解法では△ＳＤＢを利用して求めています。

大問５（確率）

（ア）　43.9％
条件が複雑。
■ルール①
大の目…ａ。小の目…ｂ
ａ＞ｂのときは差、ａ≦ｂのときは和をｎとする。
■ルール②
取るカードの和が①の結果ｎと同じにする。
取るカードの枚数はできるだけ多くする（取る数が同数なら最も大きい数をとる）。

５だけ残る→１・２・３・４を取る。
ｎ＝１＋２＋３＋４＝１０
ルール①でｎ＝１０にするには、
（ａ、ｂ）＝（４、６）と（５、５）の２通り。
注意すべきは（６、４）だとａ＞ｂだから、ｎ＝６－４＝２になってしまう。
２/３６＝１/１８　【２】

（イ）　7.8％!!
ここもむずい。
（ａ、ｂ）の組合せより、取るカードの組合せからｎの値を考える。
最小が３なので、１と２は必ず取る。
取るカードの組合せは、〔１・２〕〔１・２・４〕〔１・２・５〕〔１・２・４・５〕
〔１・２〕　ｎ＝３
（ａ、ｂ）＝（１、２）（６、３）（５、２）（４、１）
〔１・２・４〕　ｎ＝７
（ａ、ｂ）＝（１、６）（２、５）（３、４）
〔１・２・５〕　ｎ＝８
（ａ、ｂ）＝（２、６）（３、５）（４、４）
〔１・２・４・５〕　ｎ＝１２
（ａ、ｂ）＝（６、６）
以上、１１通り。　１１/３６
丁寧な場合分けと、条件に適合するよう調査。
１つでも過不足があれば失点する。

大問６（空間図形）

（ア）　73.0％
三角柱の表面積＝底面積×２＋側面積。
底面の三角形は３：４：５の直角三角形なので、ＡＣ＝５ｃｍ
３×４×１/２×２＋（３＋４＋５）×２
＝３６ｃｍ²【５】

（イ）　46.3％
断面の三角形の面積を求める。
△ＤＢＧの辺の長さを三平方を駆使して求める。

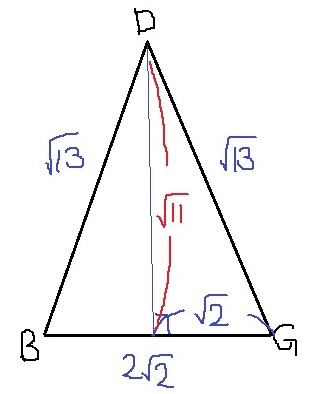
こうなる。ＤＢ＝ＤＧなので二等辺三角形。
あとは三平方で高さを出す→√１１
２√２×√１１÷２＝√２２ｃｍ²【４】

（ウ）　1.7％!!!
神奈川教育委員会は大問ごとに罠を仕掛けなければ気が済まないのか！
ＢＣの最短距離→展開図で直線の作図。

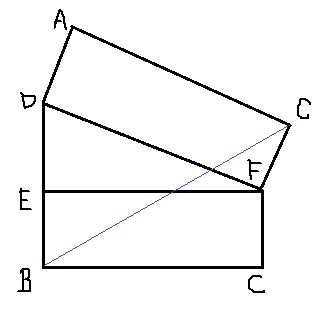
ここから次の一手が難所。
ＢＣを１辺とする直角三角形を強引に作る。

垂線を右側に引く（右下をＨとする）。
△ＤＥＦの角度で●＋●が90°だから、
右側の小さな直角三角形と相似。
斜辺をＦＣとして３：４：５を使うと上のようになる。
△ＣＢＨで三平方。
ＢＣ²＝（８/５＋２）²＋（４＋６/５）²
＝（324＋676）/２５＝1000/25＝４０
ＢＣ＝√４０＝２√１０ｃｍ
意気消沈した生徒は多いのでは…？

大問７（平面図形）

（ア）　77.5％
次の行から逆算すればいい。
ⅰ－【３】、ⅱ－【１】

（イ）　7.4％!!
ユニークな出題形式。
Ｐを動かしたとき、２つの三角形の関係性を捉える。

常に△ＡＢＱ∽△ＰＣＧが成り立つ理由。
青がＰが動く範囲。
円周角の定理と対頂角から、３つの角が常に等しくなる。
ＡＢ＝ＣＰのとき、１辺と両端角が等しくなるので合同になる。

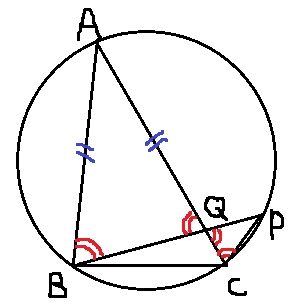
ＡＢ＝ＡＱのとき。
△ＡＢＱは二等辺で底角が一緒。
対頂角と円周角で△ＰＣＱも一緒で二等辺。

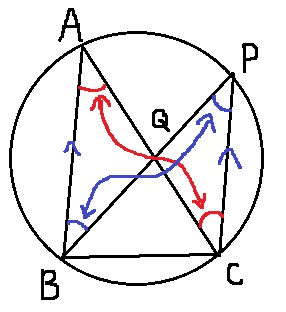
本問の答えは、ＡＢ//ＣＰ。
ダブル錯角とダブル円周角で４つの角が等しくなり、
ともに二等辺となる。

解答には「ＡＢ」を用いることが要求されている。
本問では辺の長さの情報がないので、角度が等しくなることを利用したい。
角度が等しくなる条件は平行線。
ＡＢとどこが平行になればよいか…と考えていく。

おそらく、誤答で多くなるのは〔ＡＢ＝ＢＱ〕かと思われる。

再確認。青がＰが動くところ。
Ｐがこの範囲を動くと、ＱはＡＣ上を移動する。
Ｑを移動させるとＡＢとＢＱが等しくなるときがない！
ＡＢ＝ＢＱとなるときは、ＰがＡに接するときだが、
問題文でＰは『Ａを除いた部分を動く』とあり、△ＡＢＱも形成されない。

（ウ）　2.4％!!
ラストも計算処置が面倒くさい。

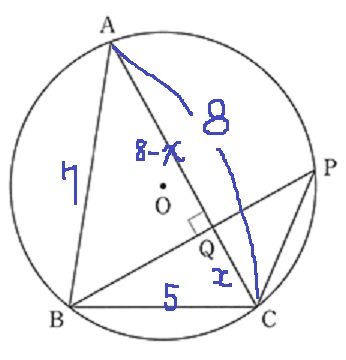
三角形のなかに直角三角形があるので△ＡＢＣ内部で三平方。
ＣＱをｘとおく。
５²－ｘ²＝７²－（８－ｘ）²
１６ｘ＝４０
ｘ＝５/２
ＡＱ＝８－５/２＝１１/２

△ＢＱＣで三平方。
ＢＱ＝５/２・√３

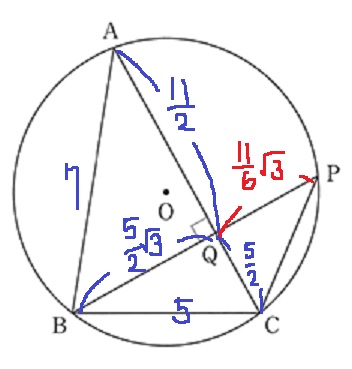
△ＡＢＱ∽△ＰＣＱ（２角が等しい）ので、
１１/２×（５/２ )/（５/２・√３）　←連分数は５/２で約分できる。
＝１１/６・√３
方べきの定理を利用して【ＡＱ×ＱＣ＝ＢＱ×ＱＰ】でも同じになる。
ＢＰ＝５/２・√３＋１１/６・√３＝１３/３・√３ｃｍ

発案できても、立式と計算に手間がかかる問題が多すぎる。
上位校は難しい特色検査もやるんだし、
みんなが受ける１日目はもう少し易しくしてもいいのでは？
あるいは、発想さえできれば計算処理が楽になるなど、
試験時間と設問の負担を考慮したバランス感覚を神奈川教育委員会は養うべきだと思う。

2019年度（神奈川）
社会…平均42.3点　理科…平均61.3点　英語…平均49.8点
数学(追検査)　その他は下記リンクの目次からどうぞです。
公立高校入試解説ページに戻る