2020年度　愛知県公立高校入試過去問Ｂグループ【数学】解説

受験者平均9.7点（前年比；－2.3点）、合格者平均10.1点（前年比；－2.3点）
問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
４－６÷（－２）
＝４＋３＝７

（２）
（２ｘ＋１）（３ｘ－１）－（２ｘ－１）（３ｘ＋１）
＝６ｘ²－２ｘ＋３ｘ－１－６ｘ²－２ｘ＋３ｘ＋１
＝２ｘ

（３）
（√５－１）²＋√20
＝５－２√５＋１＋２√５
＝６

（４）
（ｘ＋１）（ｘ－１）＝３（ｘ＋１）
ｘ²－１＝３ｘ＋３
ｘ²－３ｘ－４
＝（ｘ＋１）（ｘ－４）＝０
ｘ＝－１、４
*両辺に（ｘ＋１）が見えるからといって、両辺を÷（ｘ＋１）してはならない！
ｘ＝－１のときはｘ＋１＝０となり、０で割ることができない。

（５）
鉛筆５本…５ａ円、消しゴム１個…ｂ円
お釣りがあったということは、購入代金は500円を下回る。
５ａ＋ｂ＜500

（６）
中学受験の解き方をします。
ポイントは合計が変わらないこと。

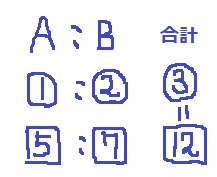
変更前は、Ａ：Ｂ＝①：②
変更後は、Ａ：Ｂ＝□５：□７
③＝□12なので、〇を４倍すれば□に統一できる。

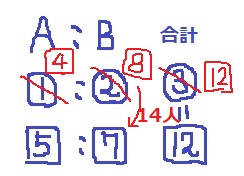
変更により、Ｂは□１減り、これが14人にあたる。
全体は□12だから、14×12＝168人

（７）
ア：ｘ≧０であれば正しいが、ｘ＜０のときはｘが増加するとｙは減少する。×
イ：ｙ軸を対称の軸として左右対称。〇
ウ：原点を通過するので、ｘ＝０のとき、最小値ｙ＝０→０≦ｙ≦４×
エ：グラフは下に凸のグラフで、ｙの最小値は０。〇
イ・エ

（８）
６人の中央値は、３番目と４番目の平均値。
23と25の平均→24ｍ

（９）

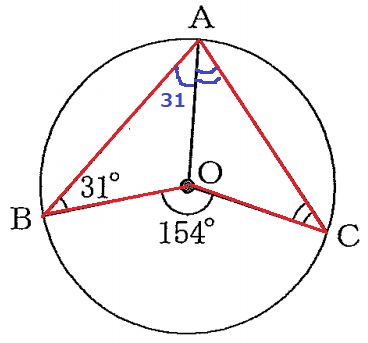
半径より、△ＡＢＯと△ＡＣＯは二等辺。
赤線でブーメラン型。
ブーメランの３つの角の和は、ブーメランの股の角。
∠ＡＣＯ＝（154－31×２）÷２＝46°

大問２（小問集合２）

（１）
サイコロの出目の出方は、６×６＝36通り

１～６までの約数を並べてしまおう。
１→１
２→１・２
３→１・３
４→１・２・４
５→１・５
６→１・２・３・６
カードを１枚に残すには、必ず６を出して４枚取らなければならない。
（４、６）（６、４）（５、６）（６、５）の４通り。
４/36＝１/９

（２）

３と128を並べてみると、最後の方は２のベキ乗のレールに乗って１にたどり着く。
操作の回数は７回で固定なので、最初の方をいじる。

１つは、〔３→10〕を〔20→10〕にチェンジ。
もう１つは、〔128→64〕を〔21→64〕にチェンジ。
ａ＝20、ｂ＝21
*本問はコラッツ予想とよばれる、数学界の未解決問題の１つ。
奇数なら３倍＋１、偶数なら÷２をすれば、どんな自然数でも最後は１になるという。

（３）

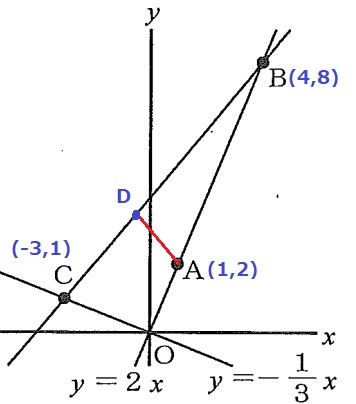
与えられた式から座標を確認。
Ａを通る、△ＢＯＣを二等分する直線とＢＣとの交点をＤとする。

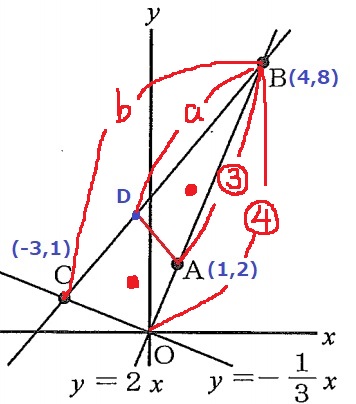
ｘ座標を頼りに辺の比を考える。
ＡＢ：ＯＢ＝３：４
ＤＢ＝ａ、ＣＢ＝ｂとする。

△ＢＡＤと四角形ＡＯＣＤの面積が等しいので、
△ＢＡＤの面積を２倍すれば△ＢＯＣとなる。
隣辺比から、ａ×③×２＝ｂ×④
⑥ａ＝④ｂ
ａ：ｂ＝４：６＝２：３

ＣＤ：ＤＢ＝１：２
Ｄのｘ座標…－３＋７×１/３＝－２/３
Ｄのｙ座標…１＋７×１/３＝10/３
Ｄ（－２/３、10/３）

＠別解＠
別解というより、問題集に出てくる王道の解き方は等積変形かと思われる。

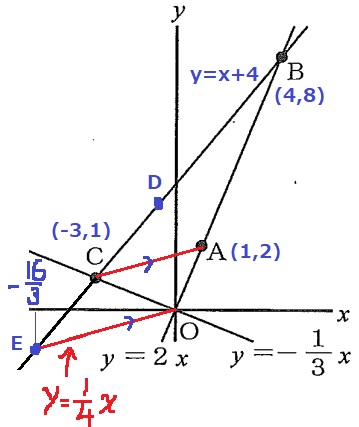
Ｏを通る、ＡＣに平行な線をひき、ＢＣとの交点をＥとする。
ＢＣを通る直線；ｙ＝ｘ＋４
ＡＣの傾きが１/４なので、ＯＥ；ｙ＝１/４ｘ
ｘ＋４＝１/４ｘ
これを解いて、Ｅのｘ座標は－16/３
ＤはＢＥの中点から、Ｄのｘ座標が－２/３
これをｙ＝ｘ＋４に代入してＤ（－２/３、10/３）

（４）①
情報整理！
Ａの40ｃｍは１分あたり２ｃｍずつＣに移動。
ポンプＰが止まるのは、40÷２＝20分後

Ｃは75ｃｍになるので、Ｂから75－40＝35ｃｍ分の水が移された。
Ｂの35ｃｍは１分あたり１ｃｍずつＣに移動。
ポンプＱが止まるのは、35÷１＝35分後

つまり、20分後にＰが止まり、その15分後にＱが止まる。
15分後

②
なかなか面白い(‘ω’)
はじめにＡとＢにどれほど水が入っているかはわからない。
→どちらのポンプが先に止まるかわからない。

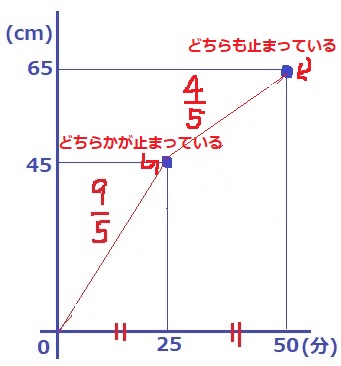
とりあえず、座標をプロットする。
最初はＰとＱを同時に動かすので、Ｃは毎分３ｃｍずつ高くなるはず。
原点から25分後の（25、45）までの傾きを調べると、45/25＝９/５
３ではなくなっているということは、25分前にいずれかのポンプが止まっている。
Ｐが先に止まる；毎分３ｃｍ→毎分１ｃｍ→０
Ｑが先に止まる；毎分３ｃｍ→毎分２ｃｍ→０
25分まではどちらか一方は動いているので、Ｑが先に止まれば傾きは２より大きいはず。
よって、先に止まるのはポンプＰ、後に止まるのはポンプＱとなる。
（ちなみに、（25、45）から（50、65）までの傾きは、20/25＝４/５
傾きが１未満ということは、最後は２つのポンプが止まっている状態である）

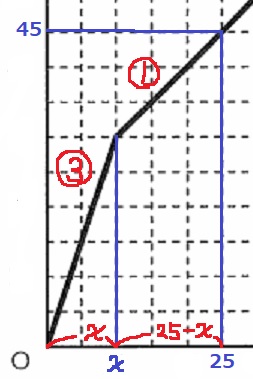
変化の割合は３ｃｍ→１ｃｍ。
ポンプＰがｘ分後に止まったとして、Ｃの高さで方程式を作成。
３ｘ＋１×（25－ｘ）＝45
ｘ＝10
ポンプＰは10分まで稼働し、そのときのＣの高さは３×10＝30ｃｍ。

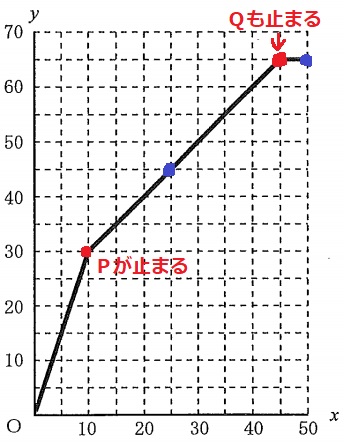
うしろの線分を延長すると（50、70）に向かい、（50、65）と交わらない。
ｙの最大値は65であり、手前の（45、65）でグラフが折れることになる。

大問３（図形）

（１）
発想力が求められる。
ＤＦが∠ＡＤＣの二等分線である点をうまく活用する。

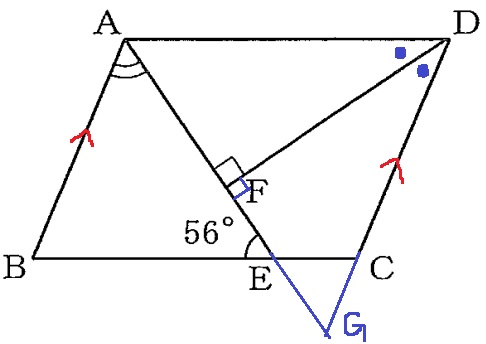
ＡＥとＤＣを延長、交点をＧとする。
△ＡＤＦと△ＧＤＦは、一辺と両端角が等しく合同。
ＤＡ＝ＤＧとなり、△ＡＤＧは二等辺となる。

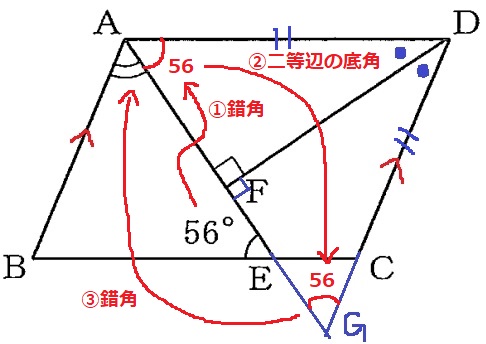
①ＡＤ//ＢＣから、錯角で∠ＡＥＢ＝∠ＥＡＤ＝56°
②二等辺三角形ＡＤＧの底角で、∠ＤＧＡ＝56°
③ＡＢ//ＤＧから、錯角で∠ＢＡＦ＝56°

（２）①
四角形ＡＥＦＤと四角形ＥＢＣＦの周の長さが等しい。

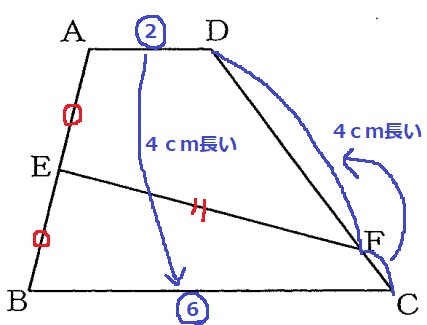
ＡＥ＝ＥＢを相殺。共通辺ＥＦも相殺。
ＢＣはＡＤより４ｃｍ長いので、ＤＦがＦＣより４ｃｍ長くなればいい。
ＤＦ＋ＦＣ＝（ＦＣ＋４）＋ＦＣ＝２ＦＣ＋４＝５ｃｍ
ＦＣ＝１/２ｃｍ
ＤＦ＝５－１/２＝９/２ｃｍ

②
いろいろなやり方があると思われる。

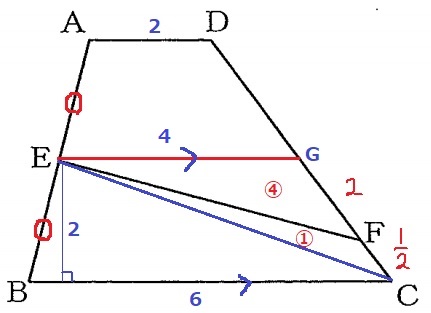
ＥＣに補助線。
四角形ＥＢＣＦを△ＥＢＣと△ＥＣＦに分割する。
△ＥＢＣの面積…ＥはＡＢの中点だから、高さは２ｃｍ。
６×２÷２＝６ｃｍ²

Ｅを通る、ＢＣに平行な線をひき、ＣＤとの交点をＧとする。
平行線と線分の比から、ＥＧはＡＤとＢＣの平均→ＥＧ＝４ｃｍ
ＧはＣＤの中点で、ＣＧ＝５÷２＝５/２ｃｍ
ＦＧ＝５/２－１/２＝２ｃｍ
△ＥＣＦ：△ＥＦＧの面積は、ＣＦ：ＦＧ＝１/２：２＝①：④
△ＥＣＦの面積…△ＥＣＧの面積の４/５倍→４×２÷２×①/⑤＝４/５ｃｍ²
四角形ＥＢＣＦの面積…６＋４/５＝34/５ｃｍ²

（３）①

組み立てると円錐台（プリン型）になる。
展開図の弧の長さから、円Ｑの直径は４ｃｍ、円Ｐの直径は６ｃｍとなる。
円Ｐと円Ｑの面積の和は、3×３×π＋２×２×π＝13πｃｍ²

②

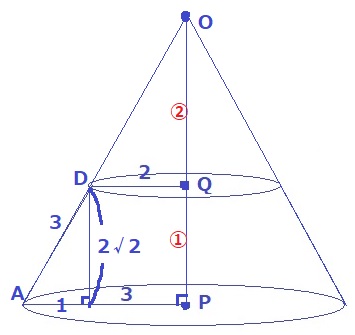
ＰＱの高さは、左側で三平方。
ＰＱ＝√（３²－１²）＝２√２
ＯＱ：ＯＰ＝ＤＱ：ＡＰ＝②：③
ＯＰ＝２√２×③＝６√２ｃｍ
体積比は辺の比の３乗。
３×３×π×６√２÷３×（３³－２³）/３³＝38√２/３ｃｍ³

大問１
（４）両辺から（ｘ＋１）を消す人いそう。
（６）算数で解いた方が処理が速い。
大問２
（２）３と128が出ているので、これらで試行する。
７回固定だから最初しかいじくらない。
（３）隣辺比に慣れておく。
（４）数量変化に推論要素が含まれている。傾きの度合いに注目する。
大問３
（２）②テクニカルゆえ差がでやすい。問題集に類題がないことはない。
（３）立体図をきちんと描くこと。∽で高さを算出。
公立高校入試解説ページに戻る