2019年度　山口県公立高校入試問題過去問【数学】解説

平均26.8点（50点満点）

問題はコチラ→リセマムさん

大問１（計算）

（１）
４×（－３）＝－12

（２）
（－２）²＋１
＝４＋１＝５

（３）
２（ａ＋５）＋（７ａ－８）
＝２ａ＋10＋７ａ－８
＝９ａ＋２

（４）
８/３ｘｙ÷（－６ｘ）
＝－４/９ｙ

（５）
５√５＋√20
＝５√５＋２√５＝７√５

大問２（小問集合）

（１）
ａ²＋４ａ－45
＝（ａ－５）（ａ＋９）

（２）
２ｘ＋３ｙ≦4000

（３）
ｎ角形の内角の和→180（ｎ－２）
180（10－２）÷10＝144°

外角から攻めてもＯＫ。
ｎ角形の外角の和→360°
180－360÷10＝144°

（４）
ｙの変域が正である→ａ＞０（グラフは下に凸）
ｘ＝２のとき、ｙ＝３となる。
３＝２²ａ
ａ＝３/４

大問３（方程式）

（１）
豆腐40ｇあたりで脂質は1.4ｇ。
100ｇあたりでは、1.4×100/40＝3.5ｇ

（２）
一次方程式でも解けるが、連立と指定されているので、
豆腐をｘｇ、牛ひき肉はｙｇとおく。
重さの合計から、ｘ＋ｙ＝120…①

気を付けるべき点は、カロリーを１ｇあたりに直しておくこと！
豆腐24kcalは40ｇあたり、牛ひき肉210kcalは100ｇあたりの数値。
ｘとｙの単位がｇなので、１ｇあたりのカロリー値を計算しておく。
豆腐…24÷40＝0.6kcal　牛ひき肉…210÷100＝2.1kcal
0.6ｘ＋2.1ｙ＝150…②

①、②を解くと、ｘ＝68、ｙ＝52
豆腐…68ｇ、牛ひき肉…52ｇ

大問４（確率）

Ａは４か５を取り出せば良い。
ア…２/５

Ｂについては答案に過程も記述する。
全体の取り出し方は、３×３＝９通り

４以上より、４未満の方が場合の数が少ない。余事象から攻める。
４未満の取り出し方は、（１、１）（１、２）（２、１）の３通り。
４以上の取り出し方は、９－３＝６通り。
６/９＝２/３
イ…２/３

Ａ；２/５、Ｂ；２/３
Ｂの方が確率が大きいので、Ｂの方が起こりやすい。
ウ…Ｂ

大問５（関数）

（１）
反比例は、ｘとｙの積が比例定数ａで一定。
いずれかを２、３、４…倍すると、
他方は１/２、１/３、１/４…倍になる。
１/４倍

（２）
ｙ＝－12/ｘの式に、ｙ＝２を放り込む。
Ａ（－６、２）

Ａ（－６、２）→Ｂ（０、３）に移動すると、
右に６、下に５だから、傾きは－５/６。
切片は－３なので、ｙ＝－５/６ｘ－３

（３）
長方形を２分割したときの、上と下の四角形の面積比を求めるので、
先に座標を確認しよう。

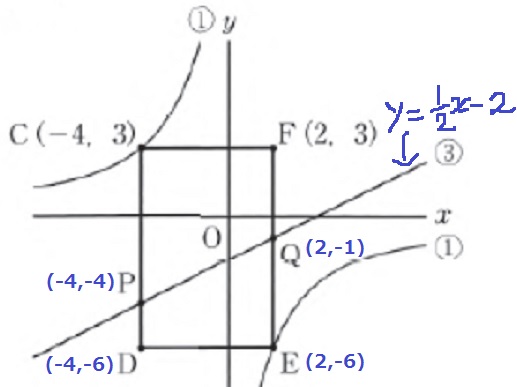
ｙ＝１/２ｘ－２に、ｘ＝－４を代入してＰ、ｘ＝２を代入してＱの座標がでる。
ｙ＝12/ｘに、ｘ＝２を代入してＥ。
Ｄは、Ｃのｘ座標とＥのｙ座標を組み合わせる。

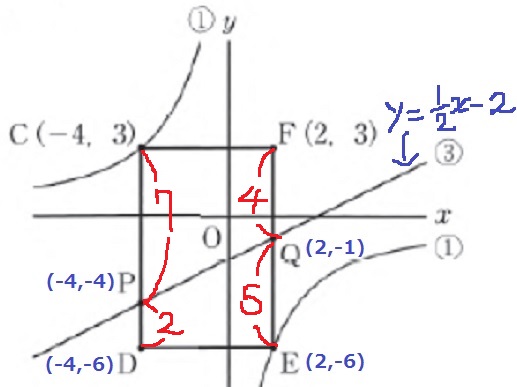
各々の長さを求める。
台形の面積比は上底＋下底の和。
四角形ＣＰＱＦ：四角形ＥＱＰＤ＝７＋４：２＋５＝11：７
よって、四角形ＣＰＱＦは四角形ＥＱＰＤの11/７倍。

大問６（空間図形）

（１）
作図問題。
折り返したらＡとＱが一致した。
折り目は対称の軸→ＡＱの垂直二等分線
これとＡＱとの交点がＰとなる。

（２）

青い部分が等しい。
半円の弧の長さは、６×２×π÷２＝６π

６πを円周とする直径は６ｃｍ。
容器を正面から見ると、１辺が６ｃｍの正三角形が見つかる。
１：２：√３より、容器の高さは３√３ｃｍ。

大問７（データの活用）

（１）
待機時間が３分なので、Ｐは30分歩いていたことになる。
1800ｍで30分だから、1200ｍは、30×1200/1800＝20分後
ｂ＝20＋３＝23分
ａ＝20、ｂ＝23

（２）ア：13
Ｂ中学校の０～1000の度数を求める。
60×45/150＝18
ｃ＝60－（18＋21＋５＋３＋０）＝13

イ：エ
「通学距離が短い階級ほど生徒の人数が多い」わけではなかったので、アは×。
150人の中央値（メジアン）は、75番目と76番目の平均値。
これは、階級の幅が1000から500に短くなっても変わらない。

表１で中央値は1000～2000ｍの階級に含まれる。
残るイ・ウ・エのなかで、イは最頻値（モード）が500～1000ｍにあるので×。
グラフに具体的な数値が書かれていないので、ウ・エの判定にやや悩むが、
表１より、０～1000ｍは45人と確定しているので、1000～1500ｍが30人を超えれば、
1000～1500の階級に中央値である75番目と76番目の平均値が含まれる。
（1000～1500の階級の30番目が全体の75番目、31番目が全体の76番目）
よって、エ。

大問８（文字式）

（１）
穴を埋めてみよう。

２ｘ＋13＝27
ｘ＝７

（２）

６段目…10ａ＋５ｂ＋32

問題は、10ａ＋５ｂ＋32の値の一の位の数が、いつも同じであることの証明。
問題文には『ｂは２以上の偶数』とある。
５に２の倍数をかけると10の倍数になるので、
10ａ（10の倍数）＋５ｂ（10の倍数）の一の位は０だから、
定数項の＋32をすれば、一の位は必ず２となる。

＠以下、公式解答より＠
ｂは２以上の偶数なので、ｎを自然数とすると、ｂ＝２ｎで表される。
10ａ＋５ｂ＋32
＝10ａ＋５×２ｎ＋32
＝10ａ＋10ｎ＋30＋２
＝10（ａ＋ｎ＋３）＋２
ａ＋ｎ＋３は自然数だから、10（10ａ＋ｎ＋３）は10の倍数である。
よって、10（ａ＋ｎ＋３）＋２の値の一の位の数は２である。
したがって、10ａ＋５ｂ＋32の値の一の位の数は、いつも同じ数２になる。
*ｂは偶数だから、はじめにｂ＝２ｎとして、ｂ→２ｎに変換する。
32は30と２に分割し、30を共通因数10に巻き込む。
すると、式の前半が10の倍数でまとめられるので、孤立した２が一の位の値となる。

大問９（平面図形）

（１）
△ＧＡＤ∽△ＧＢＦの証明。
辺の情報が乏しいので、角度で攻める。

弧ＤＥ＝弧ＥＣから、その中心角も等しい。
弧ＣＤに対する円周角とコンボさせて２角相等→∽

（２）
ＥＧ＝２ｃｍという中途半端なところの長さが与えられている。
ＥＧではなく、ＡＧを１辺とする三角形を探そう。
前問の相似を証明した△ＧＡＤはＡＧを１辺とする。
求めたいＡＦを１辺とする△ＣＡＦもなんとなく△ＧＡＤと相似に見える。

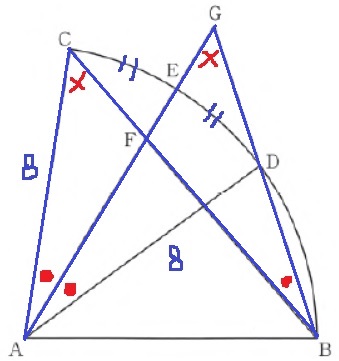
△ＣＦＡと△ＧＦＢに注目しよう。
２つの三角形の内角において対頂角を相殺すると、
蝶々型の先端の角の和は等しくなる（∠ＦＡＣ＋∠ＦＣＡ＝∠ＦＢＧ＋∠ＦＧＢ）。
∠ＦＡＣ＝∠ＦＢＧなので、∠ＦＣＡ＝∠ＦＧＢ
ここから２角が等しくなり、△ＧＡＤ∽△ＣＡＦが導ける。

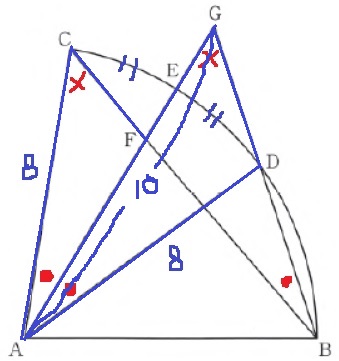
ＡＦ：ＡＤ＝ＡＣ：ＡＧ
ＡＦ＝８×８/10＝32/５ｃｍ
公立高校入試解説ページに戻る