2021年度　聖光学院中学過去問【算数】大問４解説

問題ＰＤＦ
ある平面上を点Ｐが次の〔規則１〕にしたがって移動することを考えます。

〔規則１〕
①点Ｐはまっすぐ３ｃｍ移動します。
②点Ｐは、それまで進んでいた方向から反時計回りに90度回転した方向に４ｃｍ移動します。
③点Ｐは、それまで進んでいた方向から反時計回りに〔 ア 〕度回転した方向に５ｃｍ移動します。
④点Ｐは、それまで進んでいた方向から反時計回りに〔 イ 〕度回転した方向に３ｃｍ移動します。
⑤以降、点Ｐは②～④の移動を繰り返します。

すると、点Ｐは図１のような直角三角形ＡＢＣを描きます。
このとき、次の問いに答えなさい。

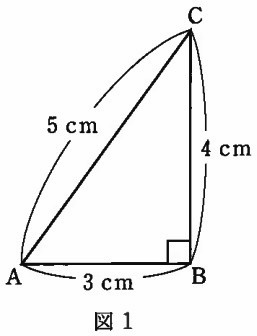
（１）
〔 ア 〕＋〔 イ 〕の値を答えなさい。

次に、同じ平面上を点Ｑが次の〔規則２〕にしたがって移動することを考えます。
ただし、〔規則２〕の〔ア〕〔イ〕と、〔規則１〕の〔ア〕〔イ〕にはそれぞれ同じ値が入るものとします。

〔規則２〕
①点Ｑはまっすぐ４ｃｍ移動します。
②点Ｑは、それまで進んでいた方向から反時計回りに90度回転した方向に３ｃｍ移動します。
③点Ｑは、それまで進んでいた方向から反時計回りに〔 ア 〕度回転した方向に５ｃｍ移動します。
④点Ｑは、それまで進んでいた方向から反時計回りに〔 イ 〕度回転した方向に４ｃｍ移動します。
⑤以降、点Ｑは②～④の移動を繰り返します。

ここで、点Ｑが①の移動をする前にいた点をＡ、移動した後に着く点をＢ、②の移動を１回した後に着く点をＣ₁、２回した後に着く点をＣ₂、・・・③の移動をした後に着く点をＡ₁、２回した後に着く点をＡ₂、・・・④の移動を１回した後に着く点をＢ₁、２回した後に着く点をＢ₂、・・・とすると、点Ｑは図２のような図形を描くことが分かります。

（２）
直線ＢＣ₁と直線Ｃ₂Ａ₂は点Ｄで交わります。ＢＤの長さは何ｃｍですか。

（３）
点Ｃ₁と点Ａ₁を結ぶ直線上の点Ｅと、点Ｃ₂と点Ａ₂を結ぶ直線上の点Ｆについて、
ＥＦの長さとして考えられる値のうち、最も小さいものは何ｃｍですか。

（４）
点Ｑが点Ａを出発してから合計2021ｃｍ移動すると、点Ｑが描く図形によって、
平面は何個の部分に分かれますか。
たとえば、点Ｑが点Ａを出発してから点Ｂ₁まで移動すると、
平面は三角形の内側と外側の２個の部分に分かれます。
また、点Ｑが点Ａを出発してから点Ａ₂まで移動すると、平面は５個の部分に分かれます。

＠解説＠
（１）

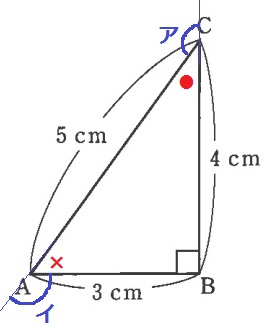
△ＡＢＣの内角より、●＋×＝90°
ア＋イ＝180×２－（●＋×）＝360－90＝270°

（２）

アとイの角度を変えないということは、●と×の同じ角度。
ここから辺の比が３：４：５の直角三角形の相似が活用できる。
Ａ₁Ｂ₁とＡ₂Ｃ₂の交点をＥとする。
ＥＢ₁＝３×３/４＝９/４ｃｍ
Ａ₁Ｅ＝４－９/４＝７/４ｃｍ

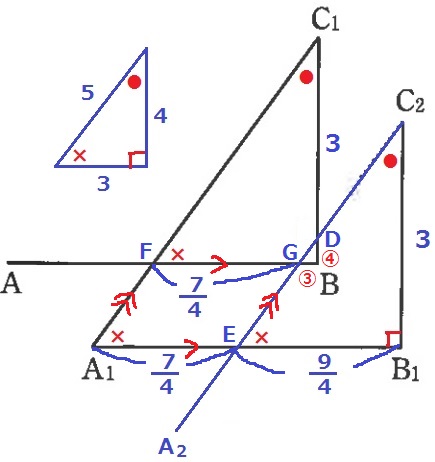
ＡＢとＡ₁Ｃ₁、Ａ₂Ｃ₂の交点をＦ、Ｇとする。
等しい同位角を頼りに、ＦＡ₁//ＧＥ、ＦＧ//Ａ₁Ｅ
→四角形ＦＡ₁ＥＧは２組の対辺が平行な平行四辺形。
対辺が等しいからＦＧ＝７/４ｃｍ

Ｃ₁Ｂ＝３ｃｍ、△Ｃ₁ＢＦと△Ｃ₂Ｂ₁Ｅは１辺と両端角が等しく合同。
ＦＢ＝９/４ｃｍ
ＧＢ＝９/４－７/４＝１/２ｃｍ

△ＧＢＤの内角も●－×－90°で辺の比が３：４：５だから、
ＢＤ＝１/２×４/３＝２/３ｃｍ

＠別解＠

Ａ₁Ｃ₁＝５ｃｍを斜辺とする直角三角形より、Ａ₁Ｅ＝３ｃｍ、Ｃ₁Ｅ＝４ｃｍ
ＥＢ₁＝４－３＝１ｃｍ
これを上にスライドしてＤＦ＝１ｃｍ
△Ｃ₂ＦＤの辺の比３：４：５より、Ｃ₂Ｆ＝１×４/３＝４/３ｃｍ

また、ＢＥ＝Ｃ₁Ｅ－Ｃ₁Ｂ＝４－３＝１ｃｍ
ＤＢ＝Ｃ₂Ｂ₁－Ｃ₂Ｆ－ＢＥ＝３－４/３－１＝２/３ｃｍ

（３）

ようは直線Ａ₁Ｃ₁と直線Ａ₂Ｃ₂の距離を求めればいい。
ＧからＡ₁Ｃ₁に垂線をひき、交点をＨとしたときのＧＨの長さを求める。

△ＧＨＦの内角も●－×－90°で辺の比が３：４：５。
ＧＨ＝７/４×４/５＝７/５ｃｍ

（４）
次のＡまで点Ｑは４＋３＋５＝12ｃｍ動くので、
2021÷12＝168…５
Ａ₁₆₈＋５ｃｍ分動く。

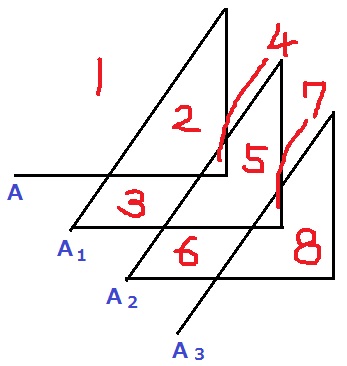
Ａ₁＝２個
Ａ₂＝５個
Ａ₃＝８個…
初項２、公差３の等差数列。
Ａ₁₆₈＝２＋（168－１）×３＝503個
余分の５ｃｍでは新たに平面を分かつことができない。
したがって、503個。

＠余談＠
では、平面が504・505・506個分かれる瞬間は点Ｑがあと何ｃｍ動いたときか？

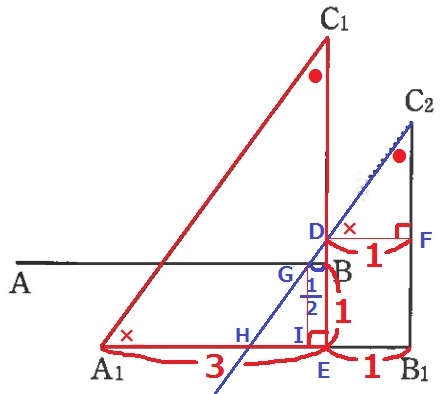
△Ｃ₁ＥＡ₁の辺の長さは、Ｃ₁Ａ₁＝５ｃｍ、Ａ₁Ｅ＝３ｃｍ、Ｃ₁Ｅ＝４ｃｍ
ＥＢ₁＝４－３＝１ｃｍ
これを上にスライドしてＤＦ＝１ｃｍ
△Ｃ₂ＦＤの辺の比より、Ｃ₂Ｄ＝１×５/３＝５/３ｃｍ

ＤＧは△ＤＢＧの辺の比から、１/２×５/３＝５/６ｃｍ

ＢＥ＝Ｃ₁Ｅ－Ｃ₁Ｂ＝４－３＝１ｃｍ
これを横にスライドしてＧＩ＝１ｃｍ
△ＧＩＨの辺の比から、ＧＨ＝１×５/４＝５/４ｃｍ

2021ｃｍはＡ₁₆₈＋５ｃｍだったので、Ｂ₁Ｃ₂上のＢの右側に点Ｑがいる。
あとは足りない部分を足せばいい。
難関中（算数科）解説ページに戻る