2023年度　高知県公立高校入試問題過去問【数学】解説

平均19.2点（前年比；＋3.0点）

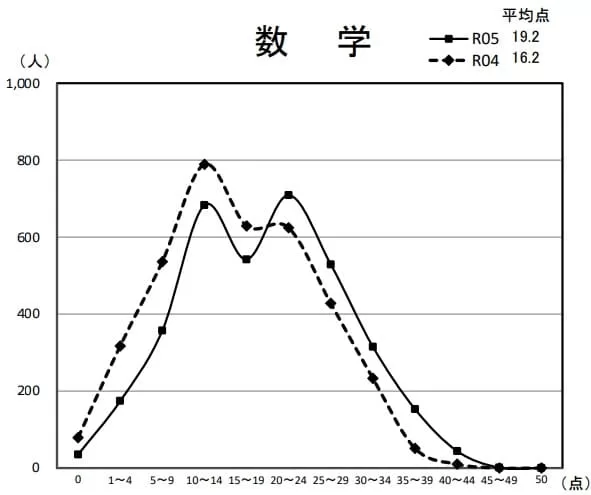
満点―０人、０点―35人
問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）①　93.9％
－５＋１－（－12）
＝－５＋１＋12
＝８

②　81.9％
（３ｘ＋ｙ）/２－（ｘ＋ｙ）/３
＝｛３（３ｘ＋ｙ）－２（ｘ＋ｙ）｝/６
＝（９ｘ＋３ｙ－２ｘ－２ｙ）/６
＝（７ｘ＋ｙ）/６

③　53.9％
－ａｂ²÷２/３ａ²ｂ×（－４ｂ）
＝６ｂ²/ａ

④　40.3％
８/√12＋√50/√６　←√12で通分
＝（８＋√100）/√12
＝18/(２√３)
＝３√３

（２）　17.0％！
生徒全員の通学時間の平均＝（生徒全員の通学時間の合計）÷（生徒全員の人数）
生徒全員の通学時間の合計＝（自転車の通学時間合計）＋（徒歩の通学時間合計）
＝23ａ＋７ｂ分

生徒全員の通学時間の平均で等式。
（23ａ＋７ｂ）分÷30人＝14分
23ａ＋７ｂ＝420
７ｂ＝－23ａ＋420
ｂ＝－23/７ａ＋60

（３）　7.7％!!
平行四辺形になるための条件。
①２組の対辺が平行（平行四辺形の定義）
②２組の対辺が等しい
③２組の対角が等しい
④対角線がおのおのの中点で交わる
⑤１組の対辺が平行、かつ長さが等しい

ア：４つの角がすべて90°→③に適合。〇
イ：１組の対辺が平行、もう１組の対辺が等しい→⑤に適合しない。×
ウ：対角線が直交する→④に適合しない。×
エ：対角線がそれぞれの中点で交わる→④〇
ア・エ

（４）　32.4％！
８ａ²ｂ－18ｂ　←共通因数２ｂ
＝２ｂ（４ａ²－９）
＝２ｂ（２ａ＋３）（２ａ－３）

（５）　35.0％
３ｘ＋２ｙ＋16＝０
３ｘ＋２ｙ＝－16　…①
２ｘ－ｙ＋６＝０
２ｘ－ｙ＝－６　…②

①＋②×２をすると、７ｘ＝－28
ｘ＝－４
②に代入、ｙ＝－２

ａｘ＋ｙ＋10＝０に（ｘ、ｙ）＝（－４、－２）を代入。
－４ａ－２＋10＝０
ａ＝２

（６）　64.7％
ネジレの位置→延長しても交わらない、かつ平行でもない。
辺ＣＦ、辺ＤＦ、辺ＥＦ

（７）　57.0％（部分点0.5％）
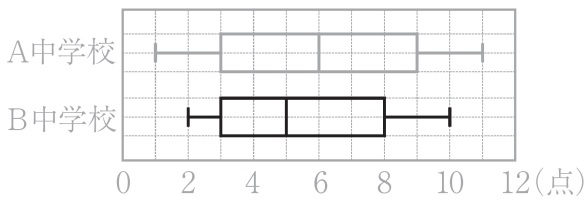
Ｂ中学のデータを昇順に並び替える。
【２・２・３・４・４・６・７・８・９・10】
最小値２点、最大値10点。
10試合の中央値は５番目と６番目の平均で５点。
第１四分位数は下位５つの真ん中、下から３番目→３点
第３四分位数は上位５つの真ん中、上から３番目→８点

（８）　40.3％（部分点0.5％）

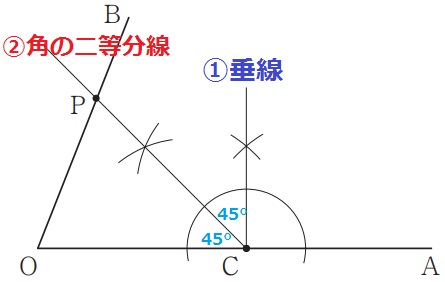
∠ＯＣＰ＝45°→ＯとＣの位置関係から、ＰはＣの左上方向にある。
90÷２＝45°から、①Ｃを通る垂線、②角の二等分線をひき、②とＯＢとの交点がＰ。

大問２（方程式）

（１）　74.5％

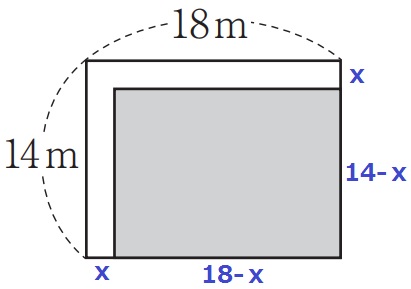
畑の区域を右下へ寄せる。
畑の縦は14－ｘｍ、横は18－ｘｍ。
ア…14－ｘ、イ…18－ｘ

（２）　58.1％

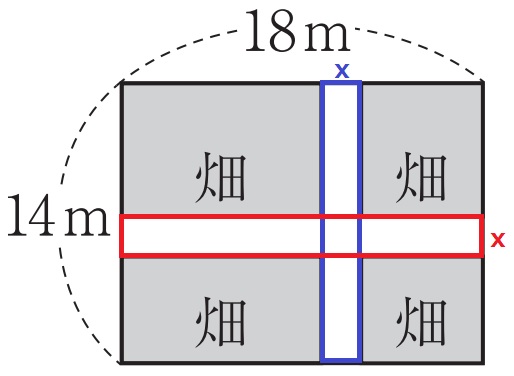
りくの考えは十字の道の縦と横をそのまま求め、交差するｘ²をひく。
縦方向の道は青の長方形…14ｘｍ²
横方向の道は赤の長方形…18ｘｍ²
ウ…14ｘ、エ…18ｘ

（３）Ｘ　30.5％！
ゆうの計算式がわかりやすい。
（14－ｘ）（18－ｘ）＝192
252－14ｘ－18ｘ＋ｘ²＝192
ｘ²－32ｘ＋60＝０

Ｙ　20.4％！（部分点9.3％、無答46.7％）
答案では途中経過を書く。
ｘ²－32ｘ＋60
＝（ｘ－２）（ｘ－30）＝０
長方形の縦の長さが14ｍなので、０＜ｘ＜14
ｘ＝２
道幅を２ｍにすればいい。

大問３（確率）

（１）　56.5％
１回目はＡ→Ｂ、２回目はＢ→Ａ。
最初のＡは６個だから、－１すれば５個になる。
→Ａから出る数が、Ａに入る数より１個多い。
すなわち、（１回目の出目；Ａから出る数）－（２回目の出目；Ａに入る数）＝１になればいい。
（１回目、２回目）＝（２、１）（３、２）（４、３）（５、４）（６、５）の５通り。
全体は６×６＝36通りだから、確率は５/36。

（２）　32.6％！
初期状態がＡ６個、Ｂ５個と、ギリギリＡ＞Ｂの状態である。
Ａ＞Ｂを維持するには１回目＝２回目（Ａ６個のまま）か、１回目＜２回目（Ａ７個以上）のいずれか。
すなわち、１回目≦２回目

１回目＝２回目（同じ出目）は１～６の６通り。
１回目＞２回目と１回目＜２回目は同じ場合の数だから、
１回目＜２回目は、（36－６）÷２＝15通り
１回目≦２回目となる組み合わせは、６＋15＝21通り
確率は21/36＝７/12

大問４（数量変化）

（１）　55.7％
蛇口ｐを開けるとＰ側の水面が上昇。
しばらくすると、水は仕切りを越えてＱ側に移る。
水面の高さは上昇→15ｃｍを維持。（アかイ）
水槽が満タンになる時間は、（20×20×25）÷100＝100秒だからイ。

＠別解＠

選択肢のグラフでは、高さ15ｃｍまでが満たされる時間は60秒後しかない。
水が入る量は一定だから、かかる時間の比も一定。
高さ15ｃｍまでの時間と高さ25ｃｍまでの時間の比は、15：25＝③：⑤
水槽が満タンになる時間は、60×⑤/③＝100秒後→イ

（２）①　8.5％!!

蛇口ｑの水量が多いので、先にＱ側が高さ15ｃｍとなる時間を求める。
高さの変化率（＝水量の比）は、Ｐ：Ｑ＝100：300＝１：３
時間は逆比で、Ｐ：Ｑ＝③：①
前問のグラフよりＰ側で高さ15ｃｍに達する時間は30秒だから、Ｑ側では30×①/③＝10秒
10秒後の様子は上図を参照。Ｐ側の水面の高さは、15×１/３＝５ｃｍ

残りの２秒間で、（100＋300）×２＝800ｃｍ³の水がＰ側に追加されるので、
12秒後のＰ側の高さは、５ｃｍ＋800ｃｍ³÷（20×10）ｃｍ²＝９ｃｍ
ｙ＝９

＠別解＠

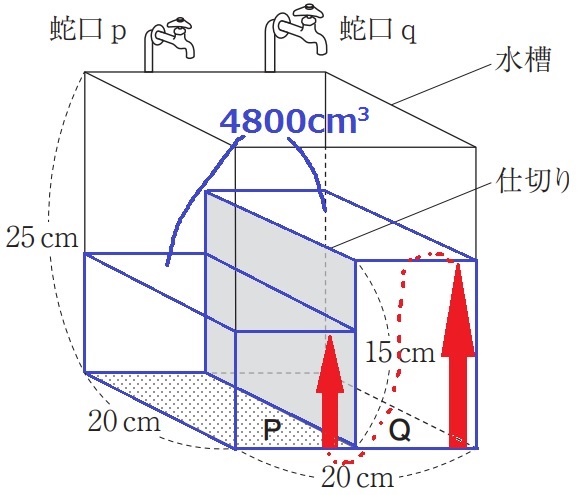
先にＱ側が埋まってから、Ｐ側に水が流れ込む。
12秒後には、（100＋300）×12＝4800ｃｍ³の水が入り、
ＰとＱの底面積は10×20＝200ｃｍ²で同じ。
Ｑの真上にＰを乗せるイメージでＱ→Ｐの順で水を埋めると、
高さは4800÷200＝24ｃｍ、Ｑ:15ｃｍのあとでＰ:９ｃｍが埋まる。

②　12.7％！
先ほどの通り、10秒後にＱからＰへ水が入る。
（１）蛇口ｐだけでは100ｃｍ³ずつ、（２）蛇口ｑも開けると400ｃｍ³ずつ水が入る。
変化率は４倍に上がるから、時間は１/４倍になる。
すなわち、仕切りの高さ15ｃｍまで満たされる時間は60÷４＝15秒後
水槽が満タンになる時間は100÷４＝25秒後

高さの変化率はｐ：ｑ＝①：③
０～10秒までは蛇口ｐだけだから、変化の割合は①
10～15秒では蛇口ｑも追加するので、①＋③＝④
15～25秒では蛇口はｐ＋ｑだが底面積が２倍に広がるので、高さの変化率は半分に落ちる。
④÷２＝②
ａ＝①、ｂ＝④、ｃ＝②だから、変化の割合はａ＜ｃ＜ｂ

大問５（関数）

（１）　78.5％
ｙ＝－１/３ｘ²にｘ＝３を代入。
ｙ＝－１/３×３²＝－３
（３、－３）

（２）　14.1％！

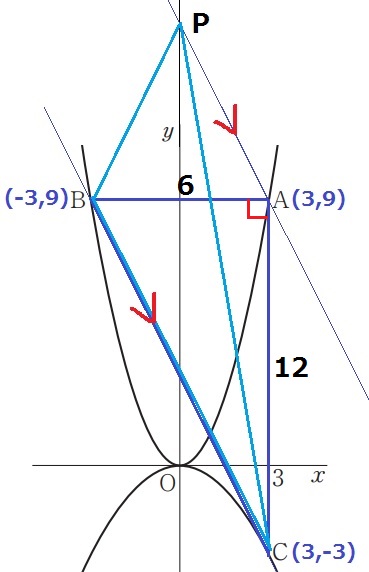
等積変形より△ＰＢＣ＝△ＡＢＣだから、△ＡＢＣを求めればいい。
Ｂはｙ軸についてＡと対称、Ｃはｘ軸についてＡと対称→∠ＢＡＣ＝90°
ＢＡ＝６、ＡＣ＝12なので、６×12÷２＝36

（３）　4.5％!!

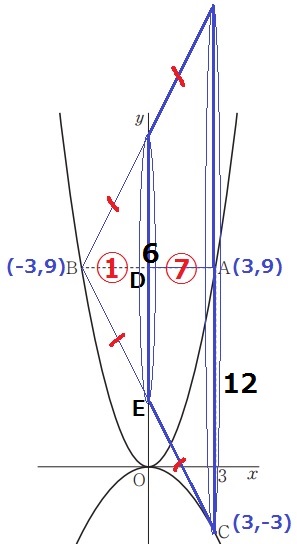
回転体は円錐台になる。
ＤがＢＡの中点であることから、相似比は小さい円錐：大きい円錐＝１：２
体積比は相似比の３乗→小さい円錐：大きい円錐＝①：⑧（円錐台の体積比は⑦）
小さい円錐を⑦倍すれば円錐台になる。
底面の半径ＤＥ＝６、高さＢＤ＝３だから、６×６×π×３÷３×⑦＝252π

＠別解＠
●パップス・ギュルダンの定理●
【回転体の体積＝断面積×重心の移動距離】

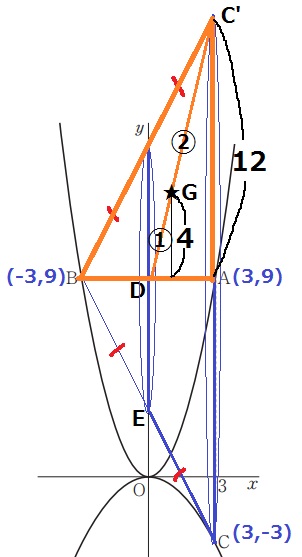
上の点をＣ’とすると、前問より断面積（△ＢＡＣ’）は36。
重心Ｇは中線Ｃ’Ｄを２：１に内分する点。
Ｇと回転軸ＢＡとの距離は、12×１/３＝４
重心Ｇの移動距離は４×２×π＝８π
パップス・ギュルダンの定理より、△ＢＡＣ’の回転体の体積は36×８π＝288π
これを×７/８倍すると252πになる。

大問６（平面図形）

（１）　1.9％!!（部分点19.6％、無答40.3％）

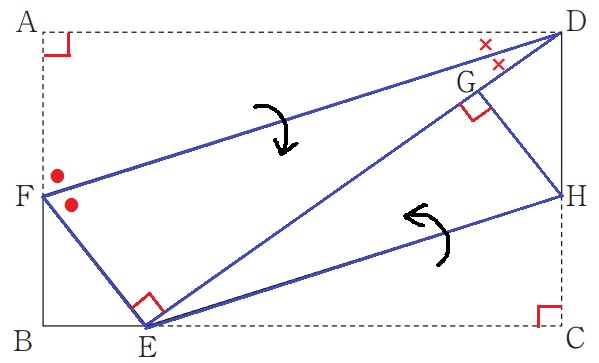
長方形の内角と折り返しから、∠ＤＥＦ＝∠ＥＧＨ＝90°
もう１つの等角をどうするか。
●＋×＝90°で調べようとしても、なかなかうまくいかない…。

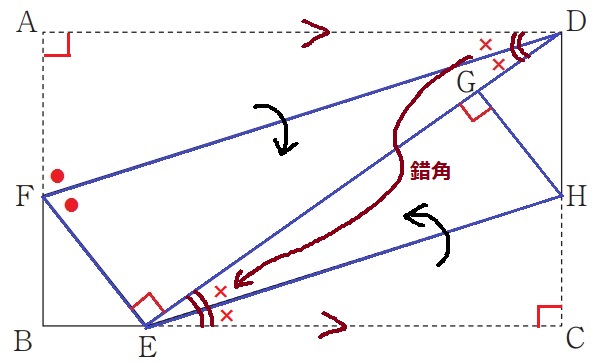
長方形の対辺は平行なので、どこかで錯角を使えないか。
ＡＤ//ＢＣの錯角で、∠ＡＤＥ（××）＝∠ＣＥＤ
折り返しで∠ＨＥＣ＝∠ＨＥＧなので、∠ＨＥＧ＝×
２角相等で、△ＤＦＥ∽△ＥＨＧ

（２）　0.5％!!!

求めたいのは△ＤＦＥ：△ＤＨＧだが、先ほどの△ＤＦＥ：△ＥＨＧを足がかりにする。
折り返し図形は合同。△ＤＦＥ：△ＥＨＧ＝△ＤＦＡ：△ＥＨＣ
ＡＤ＝15ｃｍなので、これに対応するＥＣの長さがわかれば面積比がでる。

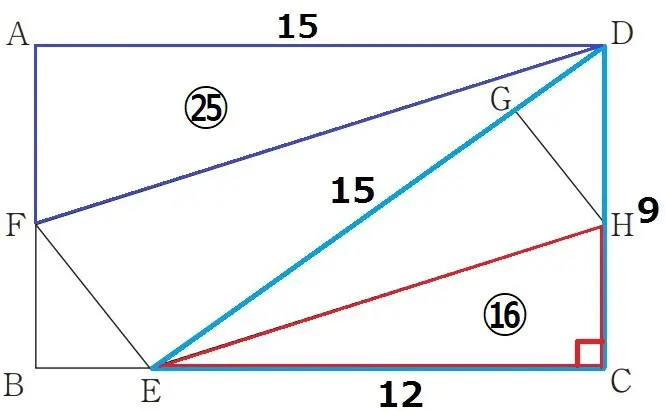
ＥＣを１辺とする△ＤＥＣに着目する。
折り返しでＡＤ＝ＥＤ＝15ｃｍ
△ＤＥＣで三平方→辺の比は３：４：５で、ＥＣ＝12ｃｍ

△ＤＦＡと△ＥＨＣの相似比は、15：12＝５：４
面積比は相似比の２乗、△ＤＦＡ：△ＥＨＣ＝△ＤＦＥ：△ＥＨＧ＝㉕：⑯

折り返しで、ＥＣ＝ＥＧ＝12ｃｍ
ＧＤ＝15－12＝３ｃｍ
△ＥＨＧ：△ＤＨＧ＝ＥＧ：ＧＤ＝４：１なので、△ＤＨＧ＝⑯÷４＝④
よって、△ＤＦＥの面積は△ＤＨＧの25/４倍。