平均29.6点(前年比;+2.3点)

問題はこちら→東進ハイスクールさん(解答)
大問1(小問集合)
(1)① 96.9%
-5+8
=3
② 82.9%
6-(-3)2×2
=6-9×2
=-12
③ 81.4%
(x+5y)/8+(x-y)/2
={(x+5y)+4(x-y)}/8
=(x+5y+4x-4y)/8
=(5x+y)/8
④ 64.3%
(4x2y+xy3)÷xy
=4x2y÷xy+xy3÷xy
=4x+y2
⑤ 75.9%
√6×√2+3/√3
=2√3+√3
=3√3
(2) 75.1%
x2-6x-16
=(x+2)(x-8)=0
x=-2、8
(3) 54.9%
5<√(6a)<7 ←2乗
25<6a<49
6の段で25より大きく、49より小さい数を調べる。
a=5、6、7、8
(4) 30.8%!
x=-2のとき、y=-4
最小値y=-16のときのxの値がaである。
-16=-x2
x=±4
-2≦x≦aだから、x=4→a=4
y=-x2は上に凸。
-2≦x≦4は原点を含むので、x=0のとき、最大値y=0
a=4、b=0
(5) 55.8%
5×5×π×144/360
=10πcm2
(*144は12の平方数)
(6)2点―35.0%、1点―38.4%
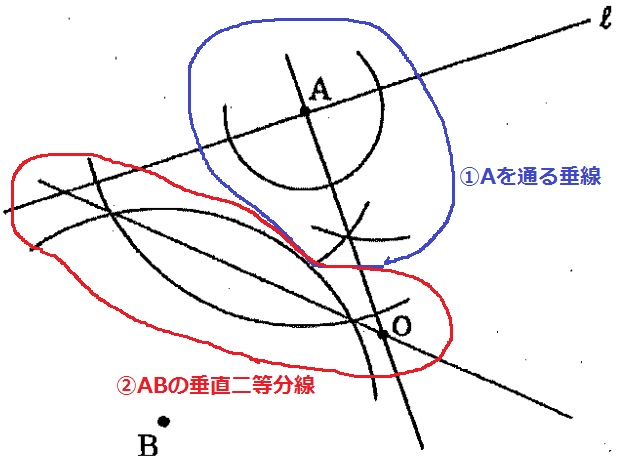
①『円は直線ℓ上でAで接する』→接線と半径は直交→Aを通る垂線
②『円はBを通る』→接点Aも通る→AとBは同一円周上にある→ABの垂直二等分線
これらの交点が中心Oである。
大問2(関数)
(1) 76.7%
y=ax2に(x、y)=(-4、4)を代入。
4=16a
a=1/4
(2) 56.2%
y=1/4x2にx=2を代入→y=1
A(-4、4)→B(2、1)
右に6、下に3だから、傾きは-1/2。
切片はBから左に2、上に1移動して、1+1=2
y=-1/2x+2
(3)① 36.6%
y=1/4x2や直線AB上の格子点も数える。
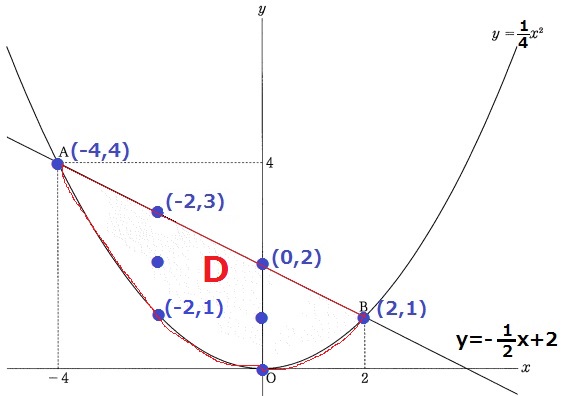
y=-1/2x+2上の格子点を調べる。
A(-4、4)から右に2、下に1移動していくと、
(-2、3)→(0、2)→B(2、1)
y=1/4x2にx=-2を代入すると、y=1
x=-2の格子点は、y=1~3の3個。
② 4.6%!!
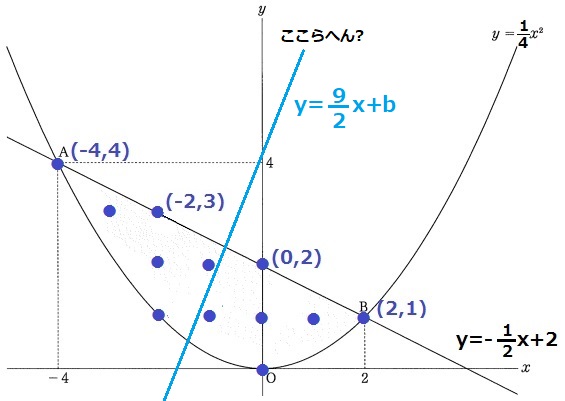
すべての格子点を追記。
格子点は計12個あるので、6個ずつに分ける。
傾き9/2は右に2、上に9で急勾配。およその見当をつけると上図のあたりか。
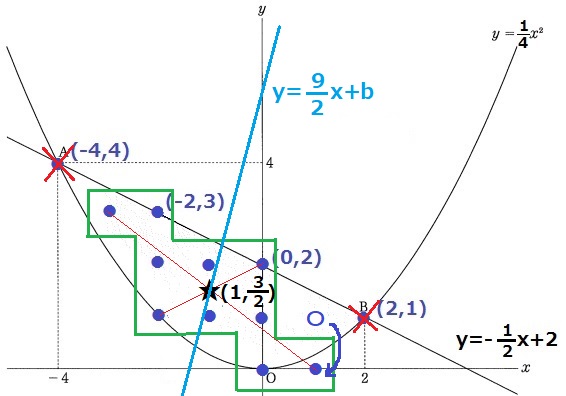
点Aと点Bは違うグループに入るので除外。
(1、1)を1つ下にズラして(1、0)にすると、格子点の並びが点対称になる。
(*ズラしても右半分にいるとわかるので影響なし)
対応する点を結んだ2直線の交点が回転の中心であり、
y=9/2x+bが回転の中心を通れば格子点を等しく分ける。
回転の中心のx座標は-1、y座標は1と2の間で3/2。
y=9/2x+bは格子点を通らないので条件適合。
傾き9/2だから、(1、3/2)から右に1、上に9/2移動して、
切片bは3/2+9/2=6
bが整数である条件をクリア。
b=6
大問3(確率・データの活用)
(1)① 82.6%
最初、一番上のカードはA。
作業を6回繰り返すと、一番上はB→C→D→E→A→B。
B
② 42.7%
【B→C→D→E→A→…】がループする。
一番上がCになるには、和が2、7、12。
●和が2→(1、1)
●和が7→(1、6)(2、5)(3、4)とこれらの逆。
●和が12→(6、6)
合計8通り。
全体は6×6=36通りだから、確率は8/36=2/9
(2)① 65.2%
四分位範囲(箱の長さ)=第3四分位数-第1四分位数
14-8=6本
②ア 71.4%
9月の第3四分位数は14本。
イ 34.0%
15本以上のフリースローを成功した割合が増えた理由を述べる。
9月の第3四分位数は14本→40人中、上から10番目と11番目の平均が14本。
15本以上は多くても25%(10人)しかない。
一方、3月の中央値(第2四分位数)は15本→上から20番目と21番目の平均が15本。
15本以上は少なくとも50%(20人)はいる。
大問4(文章題)
(1)ア…62.3%、イ…51.5%、ウ…31.4%!、エ…27.4%!
13:15~13:45の30分間はゲート1つ。
1分あたり5人通過するから、30分間では5×30=150人(ア)
今度はゲートを通過した人数(入場した人数)を求める。
最初は45人が並んでいた。
13:15~14:15の60分間では、1分あたり12人ずつ列に入る。
ゲートを通過した人数は、45+12×60=765人(イ)
(イ)がゲートを通過した人数。
(ア)がゲートが3つになる13:45までに通過した人数。
13:45以降に通過した人数は、765-150=615人(ウ)
ゲートが3つになる13:45以降は、1分あたり15人ずつゲートを通過。
615÷15=41分で入場が完了する。
その時刻は、13:45+0:41=13:86=14:26(エ)
ア…150、イ…765、ウ…615、エ…14時26分
(2) 10.1%!
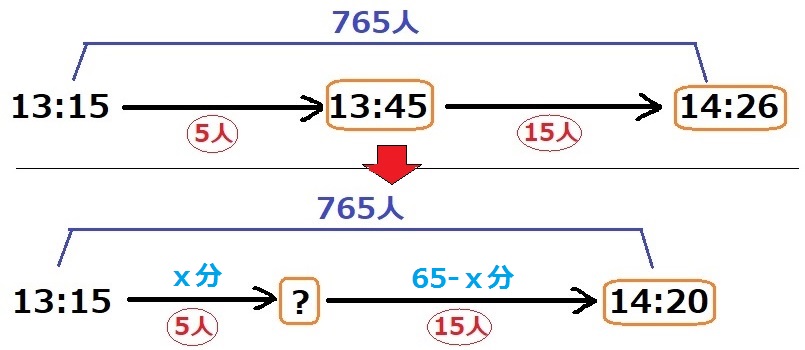
入場完了時刻を14:26から14:20に変更する。
他に変わるのは条件4『ゲートを3つに増やす時刻』だけ。
『最初は1分5人ずつ、途中で15人ずつ通過する、合計765人通過する』は変わらない。
13:15~14:20は65分間。
ゲート1つの時間をx分とすると、ゲート3つの時間は65-x分。
人数で等式を立てると、
5x+15(65-x)=765
10x=210
x=21
13:15の21分後である13時36分。
@別解@
入場完了時刻を6分前に早めたい。
この6分間では、15×6=90人がゲートを通過する。
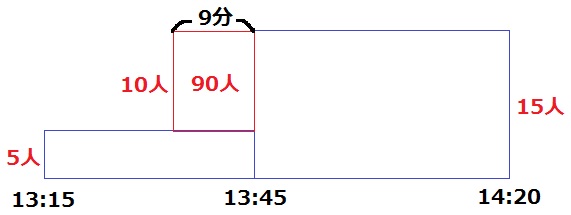
ゲートを3つに増やす13:45より前に90人を押し込む。
1分あたり押し込める人数は15-5=10人だから、90÷10=9分
13:45の9分前である13:36にゲートを増やせばいい。
大問5(空間図形)
(1) 66.8%
円柱の体積、4×4×π×10=160πcm3
*πをつけ忘れた誤答あり。
(2)① 22.4%!
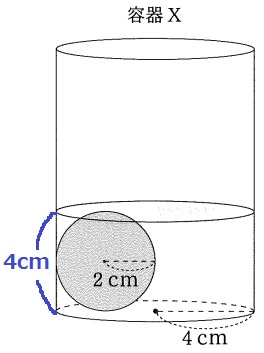
水面の高さは円の直径4cm。
水の体積は、高さ4cmの円柱から半径2cmの球を引く。
4×4×π×4-4/3π×23=160/3πcm3
*球の体積を引き忘れた誤答。
②高さ…12.6%!、体積…1.2%!!
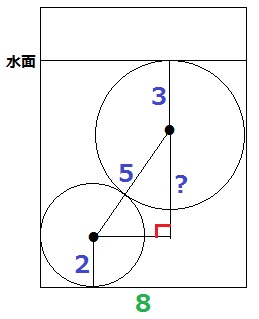
正面からみた図を作成する。
円の中心から垂線をひき、半径同士を接点で結んで直線にする。
?の長さがわかればいい。
斜辺を5cmとする直角三角形の高さが知りたい。
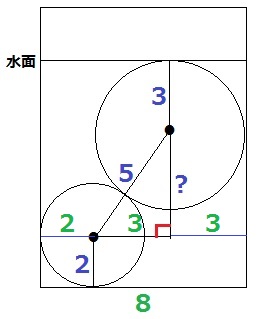
今度は横方向を調べると、底辺は8-2-3=3cm
3:4:5の直角三角形→?=4cm
水面の高さは、2+4+3=9cm
前問の状態から水を追加して、水面の高さは5cm上昇した。
追加した水の体積は、高さ5cmの円柱から半径3cmの球を引けばいい。(詳細は後述)
4×4×π×5-4/3π×33=44πcm3
高さ…9cm、体積…44πcm3
@詳細@
式で書くと以下のようになります。
①の水の体積=円柱4cm-球2cm
②の水の体積=円柱9cm-球2cm-球3cm
追加した水の体積=②の水-①の水
=(円柱9cm-球2cm-球3cm)-(円柱4cm-球2cm)
=円柱9cm-球2cm-球3cm-円柱4cm+球2cm
=円柱5cm-球3cm
大問6(平面図形)
(1)3点―36.2%、2点―5.8%、1点―15.4%、無答―23.4%
△GFH∽△ECHの証明。
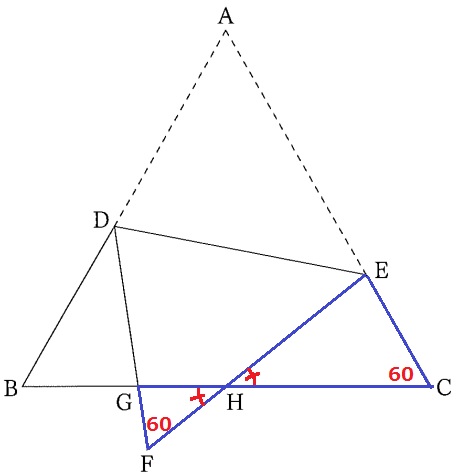
わかりやすい。
対頂角と正三角形の内角→2角相等で∽
(2)① 28.1%!
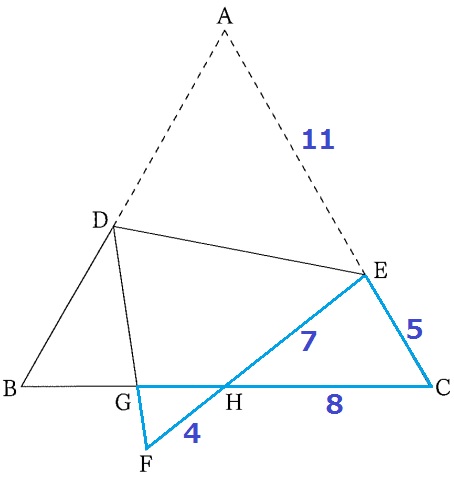
折り返しから、AE=FE=11cm
EC=16-11=5cm
先ほどの相似より、GF:EC=FH:CH=1:2だから、
FG=5÷2=5/2cm
② 6.6%!!
前問の∽から、GH=7÷2=3.5
等角を調べていくと、△GFH∽△ECH∽GBD
辺の比は5:7:8→BG=⑤、DB=⑧、DG=⑦とする。
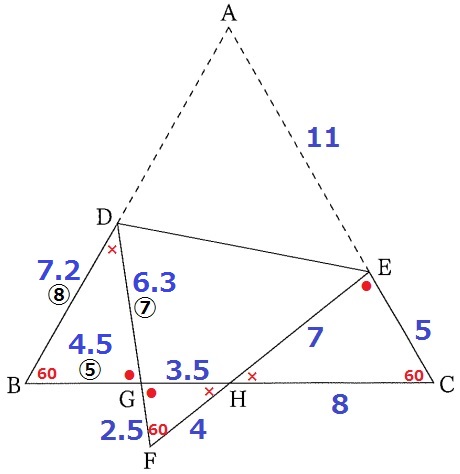
BG(⑤)=16-(3.5+8)=4.5cm
〇の数字を0.9倍すると長さになるので、DB=⑧×0.9=7.2cm
DG=⑦×0.9=6.3cm
DB:DF=7.2:(6.3+2.5)=9:11
●講評●
大問1
(1)④分配法則。
(3)2乗で根号を外して比較する。
(4)数字はxの最小値-2とyの最小値-16がわかっている。
x=-2を式に代入するとy=-4だから、y=-16のときのxがa。
(5)平方数は20×20まで言えるようにしたい。
(6)円周上にはBだけでなく、Aもある。
大問2
(2)①x=-2のとき、2つのグラフのy座標を調べる。
②解きづらい設問であった(´д`)
先にすべての格子点を記しておこう。
解説では格子点の並びを点対称に配置して、回転の中心を通ると見当をつけたが、
他に良い解き方がありましたら教えてください。
大問3
(1)一番上のカードはどのようにループするか。
(2)3月の15本は中央値。15本以上は全部員の何%か。
大問4
中学受験のニュートン算のような文章題だが、誘導にしたがって整理すれば答えを導ける。
共テの影響か問題文が長いので、ここで時間を使いすぎるのは危ない。
(2)変更する条件を見定め、方程式を立てる。
大問5
(2)①球の体積・表面積の公式も忘れずに!
②解き方のパターンは決まっている。半径の作図がポイント。
体積が厄介。式で整理すると直接求めることができるが、
無理そうなら高さ9cmの円柱から2つの球をひき、前問の答えをひいても良い。
大問6
(1)証明は平易だった。時間を残しておきたい。
(2)②相似をさらに展開する。△ECH=5:7:8をうまく使いたい。
分数より小数の方が計算がやや楽になる。



コメント