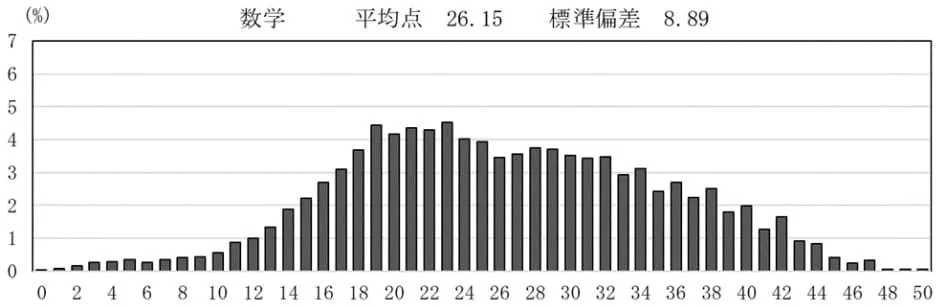
平均26.15点(前年比;+1.51点)
問題はこちら→東進ハイスクールさん(解答)
大問1(計算)
(1)ア 97.5%
-8+27÷(-9)
=-8-3
=-11
イ 84.3%
(-6a)2×9b÷12ab
=36a2×9b÷12ab
=27a
ウ 86.6%
(2x+y)/3-(x+5y)/7
={7(2x+y)-3(x+5y)}/21
=(14x+7y-3x-15y)/21
=(11x-8y)/21
エ 93.2%
√45+10/√5
=3√5+2√5
=5√5
(2) 89.9%
a2-25b2
=(a+5b)(a-5b) ←ここで代入
=(41+5×8)(41-5×8)
=81×1
=81
(3) 85.7%
x2+7x=2x+24
x2+5x-24
=(x+8)(x-3)=0
x=-8、3
大問2(小問集合)
(1) 59.6%
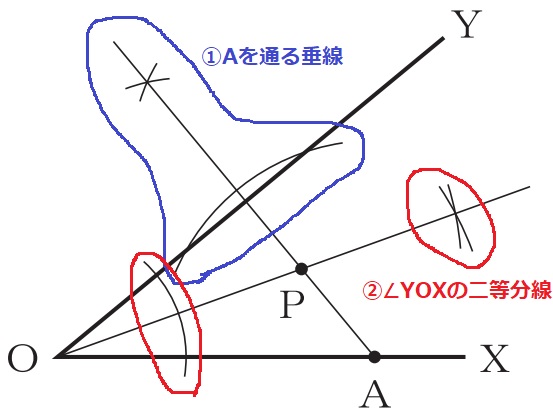
①Aを通る垂線。
②『2辺OX、OYから等距離にある』→∠YOXの二等分線
2本の直線の交点がP。
*点Aから辺OYに引く垂線の作図ができていないものが多かった。
(2) 58.5%
『p(仮定)ならばq(結論)』(p⇒q)という命題が真だとする。
(真…必ず正しい⇔偽…必ずしも正しくない)
pとqをひっくり返した命題『qならばp』(q⇒p)を逆といい、逆は必ずしも真ではない。
命題【aもbも正の数ならば、a+bは正の数である】
逆は仮定と結論をひっくり返して、『a+bが正の数ならば、aもbも正の数である』
a=-1、b=3の場合、a+b=2であるが、aが負の数なので偽。
逆…a+bが正の数ならば、aもbも正の数である。
反例…a=-1、b=3のときは成り立たない。
@逆・裏・対偶@
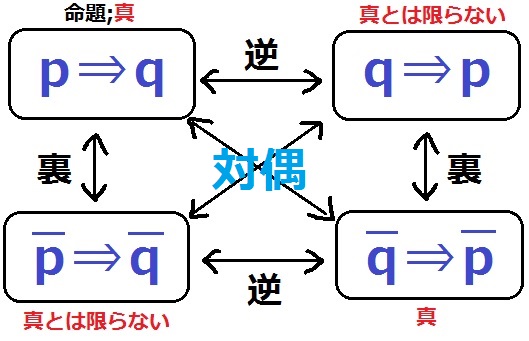
『pであるならば、qである』という命題に対して、
『pでないならば、qではない』を裏という。(pやqの上に ̄がつく)
裏も必ずしも真とは限らない。
『qでないならば、pではない』を対偶といい、
元の命題(p⇒q)が真ならば、対偶は必ず真である。
たとえば、【4の倍数であれば、2の倍数である】という真の命題に対して、
裏である【4の倍数でなければ、2の倍数でない】は反例があるので偽である。
(6や10は4の倍数でないが2の倍数である)
一方で、対偶【2の倍数でなければ、4の倍数でない】は真である。
論理形式は数式だけでなく、日本語の文章でも使えます。

ヒントとしては、A~Dの命題とその対偶をとって論理をつなげていきます。
答えが知りたい方は以下のリンク先をどうぞ。

(3) 81.3%
全体の取り出し方は、4×5=20通り
Ⅰで取り出したカードで場合分けする。
●2を取り出す→6・8・10
●3を取り出す→6・9
●4を取り出す→8
●5を取り出す→10
計7通りだから、確率は7/20。
大問3(データの活用)
(1) 78.9%
値を昇順に並べると、【7・10・12・16・23・25・26・29・32・34】
(あ)は第2四分位数(Q2;中央値)で、5番目の23と6番目の25の平均24m。
四分位範囲=第3四分位数(Q3)-第1四分位数(Q1)
Q1は下位5つの真ん中、下から3番目の12m。
Q3は上位5つの真ん中、上から3番目の29m。
Q3-Q1=29-12=17m
(あ)…24 四分位範囲…17
(2) 44.2%
Q3が29m→32mに増加している。
11人のQ2は6番目。Q3は上位5人の真ん中、上から3番目が32mである。
aが32m以上でなければ、上から3番目が32mにならない。
また、最大値は34mで変わらないから、34m以下である。
a=32、33、34
*誤答では「32、33」がみられる。
大問4(方程式)
44.6%
集めたボールペンの本数をx本、鉛筆を2x本とする。
団体Sへ送った本数…2x×0.8本
団体Tへ送った本数…2x×0.2+0.96x本
TはSより18本少なかったので、
2x×0.8-18=2x×0.2+0.96x ←100倍
160x-1800=40x+96x
24x=1800
x=75
2x=150
鉛筆…150本、ボールペン…75本
*数量関係の正しい立式ができていないものが多い。
どのような数量を文字で表しているのかを明記していないものも目立つ。
大問5(空間図形)
(1) 97.5%

左から円柱・正四角錐・円錐・球・正三角錐(正四面体)
ウ
(2) 52.0%
3×2×π×110/360
=11/6πcm
*誤答では11/4πや9πがみられる。
(3) 0.5%!!!
大問7まであるので、迷ったら後回し推奨。

DはABの中点→EはOBの中点。
正面から見た図は1辺6cmの正三角形→△OBDは1辺3cmの正三角形。
△OEDは辺の比が1:2:√3で、DE=3√3/2cm
同様に、△OEFも1:2:√3の直角三角形である。

Eから垂線をおろし、OFとの交点をHとする。
△OHE∽△OEFから、△OHEの辺の比も1:2:√3
HE=3/2×√3/2=3√3/4cm

OF⊥EH→OF⊥面DHE→OF⊥DH
△ODFの高さがDHにあたる。
DE:HE=3√3/2:3√3/4=②:①
△DHEで三平方→DH=〇√5
DH=3√3/4×〇√5=3√15/4cm
したがって、△ODFの面積は、3×3√15/4÷2=9√15/8cm2
大問6(関数)
(1) 70.8%
y=bx2(b<0)にC(4、-4)を代入。
-4=16b
b=-1/4
*誤答は4が目立つ。
(2) 41.4%
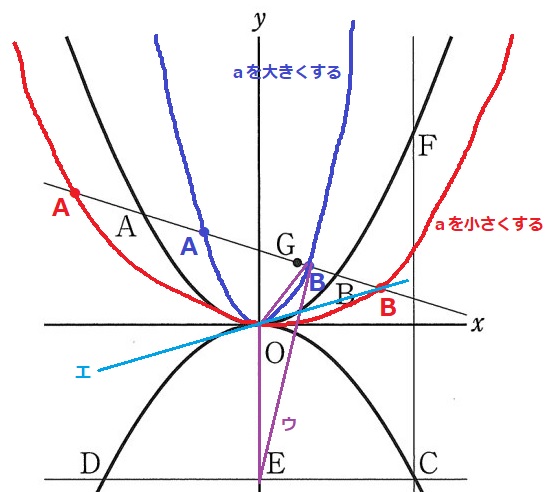
各座標をaで表しておく。
ア:aを大きくすると、グラフの開きは小さくなる。〇
イ:AとBのy座標の差は5a。aを小さくする→5aが小さくなる→y座標の差は小さくなる。×
ウ:△OBEの底辺をOE(4)とすると、高さは2。△OBEの面積は4で変わらない。×
エ:aを小さくする→4aが小さくなる→OBの傾きは緩やかになる≒小さくなる。〇
オ:aを大きくする→16aが大きくなる→Fが上に向かう→CFの長さは長くなる。×
ア・エ
*誤答はウが多い。
(3) 16.6%!
答案では求める過程も記述する。
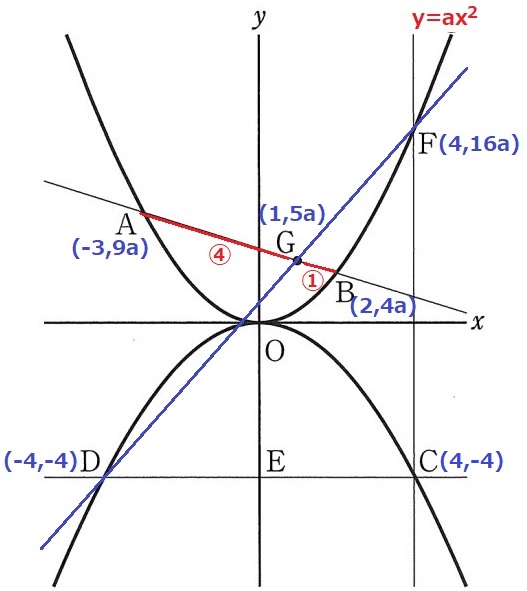
まずは座標を確定していく。
Dはy軸についてCと対称。D(-4、-4)
y=ax2にそれぞれのx座標を代入する。
A(-3、9a)B(2、4a)F(4、16a)
A・G・Bのx座標の差から、AG:GB=④:①
AとBのy座標の差⑤=5a→①=aだからB座標にaを足して、Gのy座標は5a。
(内分点の公式を知っている人は、(9a×①+4a×④)/(④+①)=5a)
G(1、5a)
最後に、DGとGFの傾きで等式を立てる。
{5a-(-4)}/{1-(-4)}=(16a-5a)/(4-1)
(5a+4)/5=11a/3
3(5a+4)=5×11a
15a+12=55a
a=3/10
*問題を解くのに必要な点座標を正しく求められていない誤答が多い。無答も多い。
大問7(平面図形)
(1) 26.0%!
△BCG∽△ECFを証明。
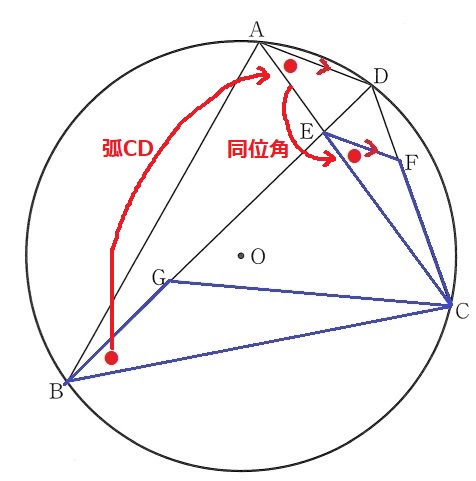
1つは弧CDとAD//EFの同位角。
もう1つは二等辺三角形の底角が集まるCに注目する。
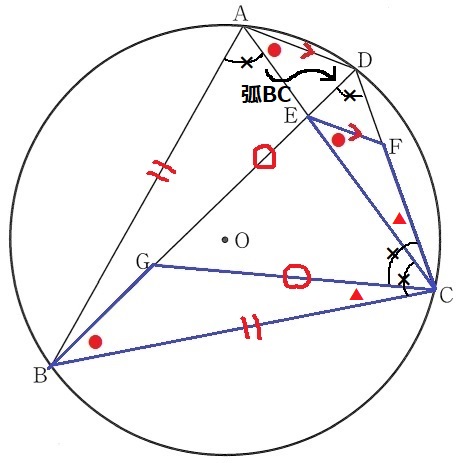
二等辺三角形ABCの底角を×とする。
弧BCの円周角から∠BAC=∠GDCとなり、二等辺三角形DGCの底角も×である。
∠ACB=∠DCGから、あいだの角の∠ECGをひくと∠BCG=∠ECF(▲)が導ける。
2角相等で∽。
*∠GBC=∠FECは説明されているが、もう1組の等角の指摘に誤りのある誤答が目立つ。
(2) 3.8%!!
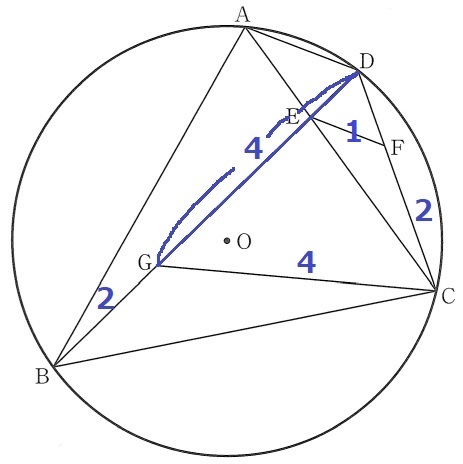
GD=GC=4cm
EDの長さがわかれば、GEが求まる。
BG=6-4=2cm
前問の相似から、BG:GC=EF:FC=1:2
EF=1cm
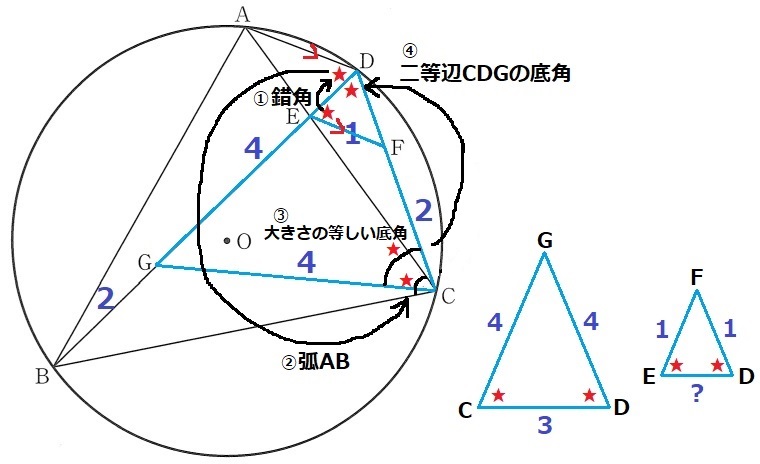
∠DEF=★とする。
AD//EFの錯角→弧ABの円周角で∠ACB=★
前問の証明で触れたとおり、∠ACB=∠DCGだから二等辺GCDの底角につないで∠EDF=★
△FEDは底角が等しい二等辺三角形。FD=1cm
△GCD∽△FEDより、ED=3×1/4=3/4cm
したがって、GE=4-3/4=13/4cm
*目測で求めたと思われる3という誤答が目立つ。
●講評●
大問1
時間がないので、手早く処理したい。
大問2
(2)反例が1つでもあれば命題は偽となる。
大問3
(2)上から3番目を32mにする。
大問4
ここから手間のかかる設問が登場する。
高得点を狙うには、条件の把握に時間をかけすぎないようにしたい。
ボールペンの2倍が鉛筆なので、ボールペンをxとおくと式が立てやすい。
大問5
(3)正面と上から見た図で図形の特徴を理解する。
△OEDは正三角形の半分で、これを手前に倒すと△OEFになる。
数値がきれいではなく、処理も問われる。解説では比を使って分数の三平方を回避した。
大問6
(2)すべて選べなので完全解答式か。
おまけに、選択肢の並びが大→小→大→小→大(#^ω^)
(3)記述ゆえ時間がかかりやすい。
DG・GFが一直線上→DGとGFの傾きが等しい。
A、Bの座標と4:1からGの座標をaで示す。
大問7
(1)等しい角からあいだの角をひく。
記述すべき要素も多くて時間がかかり、実力差も出やすい。
(2)制限時間との戦いでシビア。
前問の等角から3つ目の小さい二等辺三角形が見つかる。


コメント