平均31.9点(60点満点、前年比;+7.2点)

問題はこちら→リセマムさん
大問1(小問集合)
(1)① 98.4%
2-6
=-4
② 87.9%
-3×(-22)
=-3×(-4)
=12
③ 88.2%
(2a+b)/3+(a-b)/2
={2(2a+b)+3(a-b)}/6
=(7a-b)/6
④ 91.7%
xy2×x2÷xy
=x2y
⑤ 79.2%
6/√3+√15×√5
=2√3+5√3
=7√3
(2) 79.6%
x2+7x-18
=(x+9)(x-2)=0
x=-9、2
(3) 90.6%
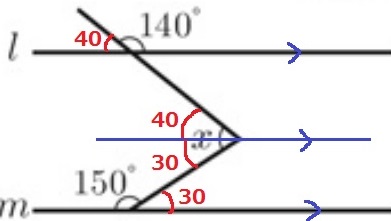
平行線をひき、同位角や錯角で集める。
x=70°
(4) 67.0%
a2-6a+9
=(a-3)2 ←代入
=(√5+3-3)2
=5
(5) 44.2%
円錐の高さは、母線5cmを斜辺とする3:4:5の直角三角形→4cm
3×3×π×4÷3=12πcm3
(6)2点-53.8%、1点-22.9%

①∠Aの二等分線。BCとの交点がP。
②AとPが重なる折り目→APの垂直二等分線。
垂直二等分線は対称の軸でAとPが対応する関係になる。
大問2(小問集合2)
(1)① 70.9%
それぞれの硬貨の結果は表か裏かの2択。
2×2×2=8通り
② 43.0%
500以下より、500超の場合が少ない。
500超のパターンは、550・600・650の3通りしかない。
500以下は8-3=5通り
確率は5/8
(2)① 64.6%
12~15冊は10人。
相対度数は小数で求めよう。
10÷40=0.25
② 36.8%
16冊は15冊以上18冊未満の階級に含まれる。
15冊以上借りた人は19人いるので、はなこは上位20人に入っているので正しくない。
*平均値と順位は話が異なる。
大問3(関数)
(1) 83.1%
y=ax2にA(3、3)を代入。
3=9a
a=1/3
(2) 42.8%
y=1/3x2に代入。
x=3のとき、y=3
x=5のとき、y=25/3
変化の割合=(yの増加量)÷(xの増加量)
=(25/3-3)÷(5-3)=8/3
@別解@
y=ax2において、xの値がpからqまで増加するときの変化の割合はa(p+q)
1/3×(3+5)=8/3
(3) 18.8%!

赤い直角三角形は合同。
AとBの座標の差から、横は2、縦は16/3。
Cはy軸上の点なのでx座標は0。Dのx座標は0-2=-2
Dのy座標は、1/3×(-2)2=4/3
Cのy座標は、4/3+16/3=20/3
大問4(数量変化)
(1) 72.8%
Aの方法は、お湯を使うまでの時間と保温時間が一緒。
表2は使わない。表1の『1時間あたり0.9円』から、y=0.9x
(2)3点-13.6%!、2点-28.3%
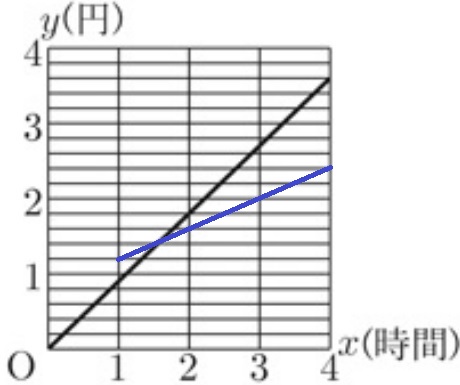
x=1のとき、3分間沸かすから、y=0.4×3=1.2
以降1時間ごとに湯を沸かす時間は1分間伸びるので、電気代は0.4円ずつ増加する。
グラフは(1、1.2)を通る傾き0.4の一次関数。
縦軸の1目盛りは0.2なので、1時間に2目盛りずつ増える。
(3) 18.1%!
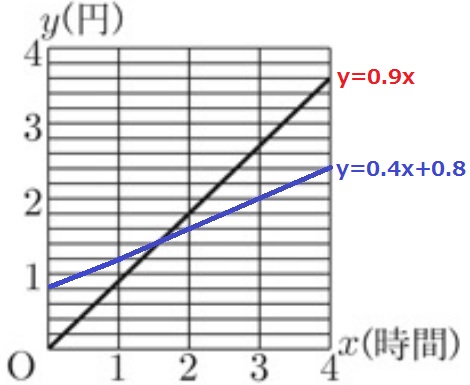
先ほどのグラフを左に延長して、切片は0.8。
y=0.9xとy=0.4x+0.8の交点を求める。
0.9x=0.4x+0.8
x=8/5
1・3/5時間=1時間36分
大問5(空間図形)
(1)① 64.4%
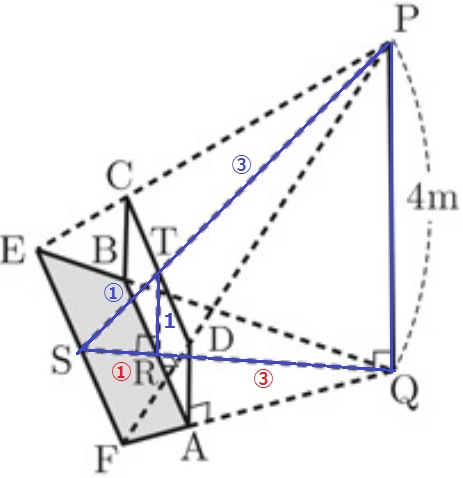
2角が等しく、△PSQ∽△TSR
PS:TS=PQ:TR=④:①
QR:RS=PT:TS=③:①
QR=3mなので、RS=3×1/3=1m
② 3.6%!!
前問のQR:RS=3:1は、本問も維持される。
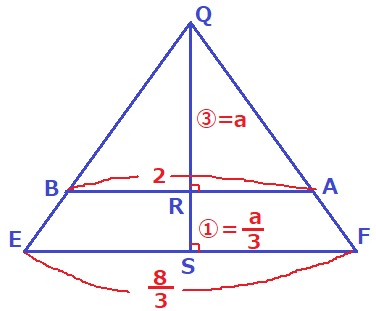
RS=a×1/3=a/3m
△QBA∽△QEF
辺の比は高さの比と等しく、BA:EF=QR:QS=③:④
EF=2×3/4=8/3m
台形ABEFの面積は、(2+8/3)×a/3÷2=7/9am2
(2) 4.0%!!
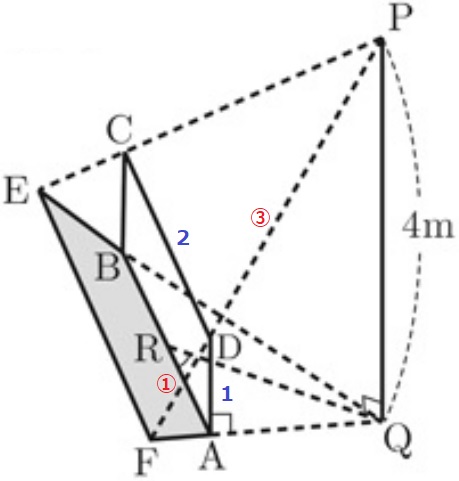
△PFQ∽△DFAより、PF:DF=④:①
△PCD∽PEFより、CD:EF=③:④
EF=2×4/3=8/3m
大問6(平面図形)
(1)3点-41.4%、2点-5.6%、1点-15.5%
△ADF∽△BCFの証明。
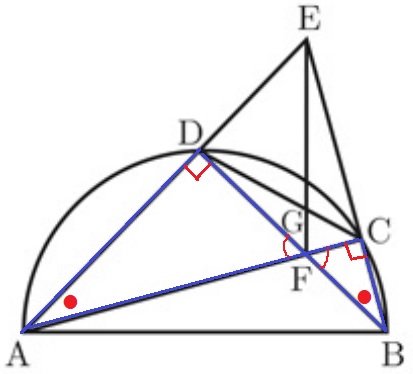
1つは対頂角。もう1つは円周角。
2角相等で∽
(2)① 30.6%!
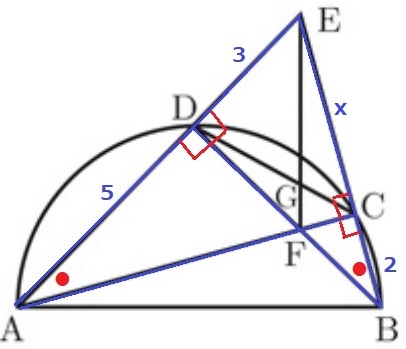
先ほどの相似で、対応する角●に注目する。
これと∠Eもしくは直角から、2角相等で△ACE∽△BDE
求めたいCEをxとおいて、
AE:EC=BE:ED
8:x=x+2:3
内項と外項の積で、x(x+2)=24
x2+2x-24
=(x+6)(x-4)=0
x>0より、x=4
4cm
② 0.4%!!!
難しい。
EGが中途半端な位置にある。
ひとまず直角三角形の斜辺にあたるEFが求まりそう。
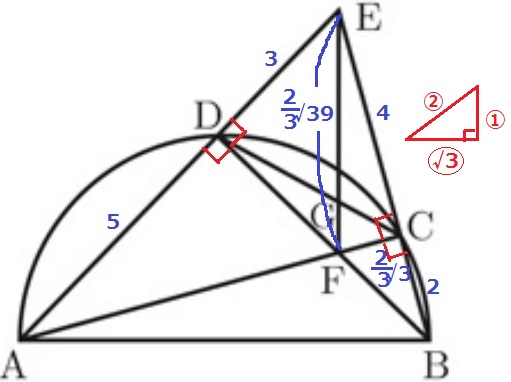
直角三角形ACEの辺の比に注目すると、AE:EC=8:4=2:1
直角三角形BDEの辺の比も、BE:ED=6:3=2:1
ここから、△ACEと△BDEは1:2:√3の直角三角形であり、
これらと相似関係にある△ADFと△BCFの辺の比も1:2:√3である。
FC=2×1/√3=2√3/3cm
△CEFで三平方。
EF2=42+(2√3/3)2=156/9
EF=2√39/3cm
ここからどうやってEG:GFを出すべきか(-_-;)
四角形CEDFは対角の和が180°で内接四角形。
4辺の長さはでるので、対角線DCとEFで分けられた4つの三角形の相似比を
統一してもできそうだが面倒くさい。
そこで、直角三角形の辺の比1:2:√3を活用する。
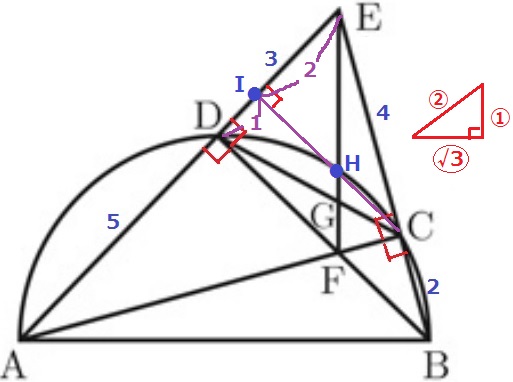
CからDEに向けて垂線。EF、EDとの交点をそれぞれH、Iとする。
△CEIも1:2:√3の直角三角形。EI=4÷2=2cm、ID=3-2=1cm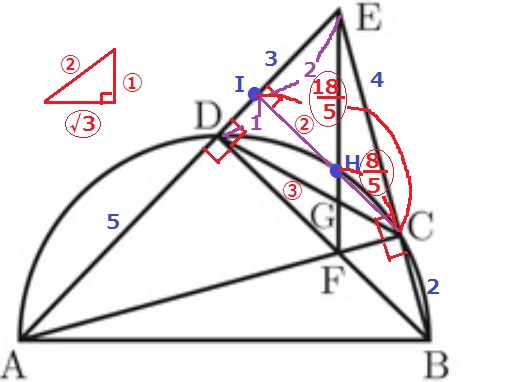
同位角が等しく、IC//DF。
△EIH∽△EDFより、IH=②とすると、DF=③となる。
また、△ADF∽△AICより、IC=③×6/5=〇18/5
HC=〇18/5-②=〇8/5

△CHG∽DFGより、HG:GF=CH:DF=8/5:3=⑧:⑮
再び△EIH∽△EDFに戻り、EH:HF=2:1だから、EH=㉓×2=㊻
したがって、EG=2√39/3×〇54/〇69=12√39/23cm
●講評●
大問1
全問とろう。
(5)よくあるパターンなので、もう少し正解したい。
大問2
(1)②確率は基本レベル。
(2)②16冊がどの階級に属するか。上から数えて少なくとも何番目か。
大問3
(3)2020年富山大問2にも似たような問題がある。
大問4
問題文が長いが、必要な情報は少ない。
(3)題意をくみとれれば計算はしやすかった。
大問5
(1)②前問はQR=3mでこちらはQR=amだから、
別問だと判断した生徒は少なくないかもしれない…。
混乱を誘発しやすい設問だったと思う。
大問6
(2)ここまで解ければ十分。
(3)難問:;(∩´_`∩);:
もっとうまいやり方があるかも。。できなくても問題無い。
1:2:√3を使うしかないと思うが、なぜCからDEに向けて垂線を引こうとしたのか、
と尋ねられるとサボもうまく答えられない。やってみたら運良くできました。。



コメント