2022年度　京都府公立高校入試・前期過去問【数学】解説

問題はコチラ→ＰＤＦファイル
2022年度・京都（中期）数学の解説はコチラ。

大問１（小問集合）

（１）
（－５）²－２³÷４
＝25－８÷４
＝25－２
＝23

（２）
３/２ａｂ÷１/６ａｂ²×（－ａ²ｂ）
＝－９ａ²

（３）
√６×√18－９/√27
＝√６×（√６×√３）－９/（３√３）
＝６√３－√３
＝５√３

（４）
３ｘ－（ｙ＋８）＝12　…①
ｘ－２ｙ＝０　…②

①を整理して、３ｘ－ｙ＝20　…③
②を整理して、ｘ＝２ｙ　…④
④を③に代入すると、
３×２ｙ－ｙ＝５ｙ＝20
ｙ＝４
最後に④に放り込む。ｘ＝２×４＝８
ｘ＝８、ｙ＝４

（５）
ｙ＝－７/３ｘ＋５
傾きａは変化の割合。
*変化の割合＝（ｙの増加量）÷（ｘの増加量）
一次関数は変化の割合が一定なので、
６×（－７/３）＝－14

（６）
（ｘ－ｙ）²－49
＝（ｘ－ｙ）²－７²
＝（ｘ－ｙ＋７）（ｘ－ｙ－７）

（７）
４ｘ²－４ｘ－１＝０
解の公式を適用。
ｘの係数が偶数なのでｂ＝２ｂ’が使える。
ｘ＝（１±√２）/２

（８）
円錐の側面積である扇形の中心角は〔×半径/母線〕。
円錐の側面積
＝母線×母線×π×半径/母線
＝母線×半径×π
これが上下で２つある。
５×３×π×２＝30πｃｍ²

（９）
平均点…（０×14＋１×13＋２×12＋３×２＋４×１）÷42＝47÷42＝47/42点
中央値（メジアン）…42人の中央値は21番目と22番目の平均で１点
最頻値（モード）…最も度数が大きい値で０点
ウ＜イ＜ア

大問２（確率）

（１）
●１で等しくなる
１を取り出す確率は２/５。
１を２連続で出す確率は、２/５×２/５＝４/25
●３で等しくなる
同様。４/25。
●５で等しくなる
５の確率は１/５。
５の２連続は、１/５×１/５＝１/25
よって、同じ数が出る確率は、４/25＋４/25＋１/25＝９/25

（２）
５個から２個を取り出す組み合わせは、₅Ｃ₂＝10通り
ａで場合分け。
●ａ＝０
ｂ＝０だが、和が０はない。
●ａ＝１
ｂ＝４＝１＋３
留意点はａ＝１なので、白玉は１つだけである！
（白１、黒３）（白３、黒１）の２通り。
●ａ＝２
ｂ＝８＝３＋５
白玉は２つなので、（白３、白５）の１通り。
玉は２個しか取り出さないからａ≧３はない。
合計３通り。確率は３/10。

大問３（関数）

（１）
ｙ＝ａｘ²にＡ（－３、２）を代入。
２＝９ａ
ａ＝２/９

（２）
ｙ＝２/９ｘ²にｘ＝６を代入してＢ（６、８）。
Ａ（－３、２）→Ｂ（６、８）
右に９、上に６だから、傾きは６/９＝２/３
Ａから右に３、上に２移動して、切片は２＋２＝４
ｙ＝２/３ｘ＋４

（３）
ＢＣ+ＣＤの長さが最小⇒線対称。

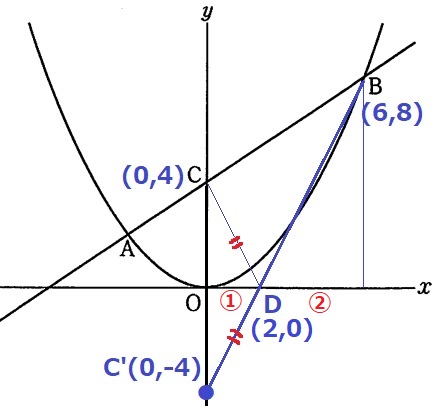
ｘ軸についてＣを対称移動させたＣ’とＢを結び、ｘ軸との交点がＤである。
ｘ座標の差から、Ｃ’Ｄ：ＤＢ＝２：４＝①：②
Ｄのｘ座標は、６×①/③＝２
Ｄ（２、０）

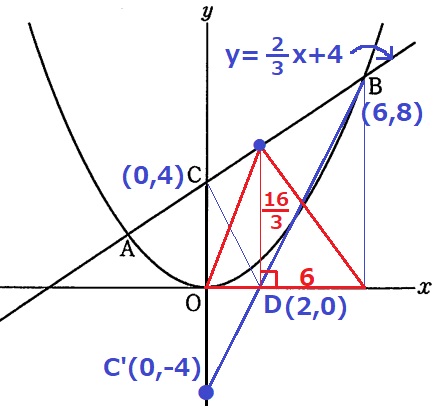
高さはｙ＝２/３ｘ＋４にｘ＝２を放り込んでｙ＝16/３
△ＢＣＤの面積は、６×16/３÷２＝16

大問４（平面図形）

（１）
△ＡＢＤ≡△ＡＣＥの証明。

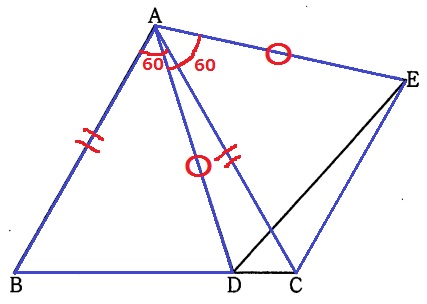
正三角形の１辺より、ＡＢ＝ＡＣ、ＡＤ＝ＡＥ
∠ＢＡＤ＝60－∠ＣＡＤ＝∠ＣＡＥ
２辺とあいだの角度が等しいので合同。

（２）

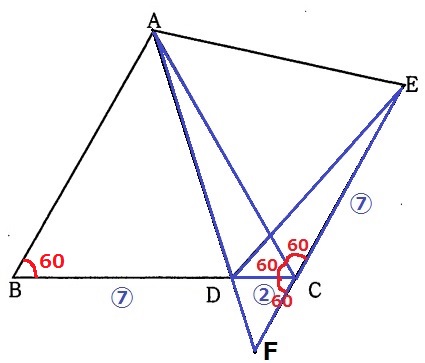
ＣＥ＝ＢＤ＝⑦
ＣＦが〇いくつになるかわかればいい。ＣＦを１辺とする三角形を観察。
・・なんとなく△ＡＣＦと△ＥＣＤの形が似ていて相似っぽい。
正三角形ＡＢＣの内角で、∠ＡＣＢ＝60°
前問の合同から、∠ＡＣＥ＝∠ＡＢＤ＝60°
∠ＡＣＦ＝∠ＥＣＤ＝120°だから、もう１個の等角さえ指摘できれば証明できる。

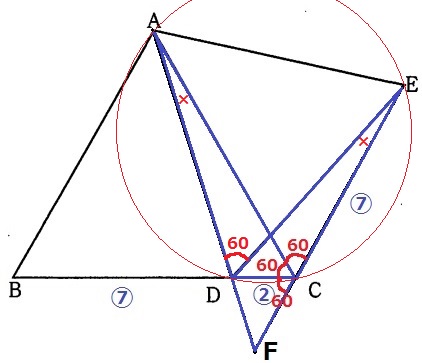
ここで∠ＡＤＥ＝∠ＡＣＥ＝60°に注目。
ＡＥについて同じ側にあって、これらの角が等しいということは、
円周角定理の逆より４点Ａ、Ｄ、Ｃ、Ｅは同一円周上にある！
弧ＤＣの円周角を使って、∠ＤＡＣ（ＦＡＣ）＝∠ＤＥＣなので２角相等。
やはり、△ＡＣＦ∽△ＥＣＤであった。

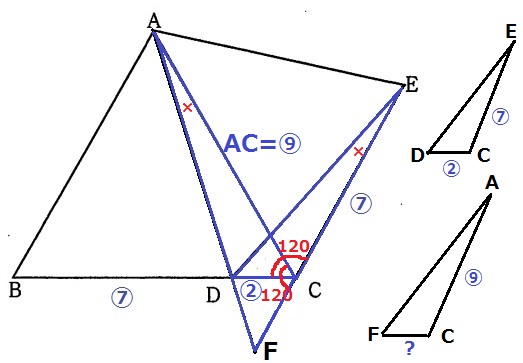
ＡＣ＝ＢＣ＝⑨
ＡＣ：ＣＦ＝ＥＣ：ＣＤだから、
ＣＦ＝⑨×２/７＝〇18/７
ＥＣ：ＣＦ＝⑦：〇18/７＝49：18

＠別解＠

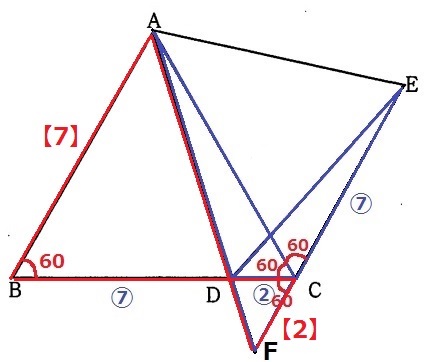
△ＣＤＦ∽△ＢＤＡを経由してもいけます。
相似比は②：⑦なので、ＣＦ＝【２】、ＢＡ＝【７】
ＢＡ：ＣＦ＝７：２だから、あとは〇の比に乗り換えて先ほどのようにＢＡ＝⑨からＣＦを求めます。

大問５（空間図形）

（１）
△ＥＩＪは直角二等辺三角形。
辺の比は１：１：√２→ＩＪ＝２√２ｃｍ

（２）

ＤＪとＢＩを延長、交点をＯとする。
三角錘Ｏ―ＥＩＪ∽三角錘Ｏ―ＡＢＤで相似比は１：２。
ＯＥ＝２√３ｃｍ
△ＡＢＤの辺の比は１：１：√２→ＢＤ＝４√２ｃｍ

ＢＤの中点をＰとする。
直角二等辺ＡＢＤを２等分するＡＰの長さは、４√２÷２＝２√２ｃｍ
△ＡＯＰで三平方→ＯＰ＝２√14ｃｍ

最後に、△ＯＢＤから面積比で四角形ＢＤＪＩを求める。
４√２×２√14÷２×③/④＝６√７ｃｍ²

（３）

Ｋの位置を調べる。
Ｋは直線ＡＧと四角形ＢＤＪＩの交点。
直線ＡＧを含む面ＡＥＧＣで切り取るとＫの位置が探りやすい。

四角形ＢＤＪＩとＡＣとの交点は先ほどのＰ。
四角形ＢＤＪＩとＥＧとの交点をＱとする。
ＰとＱはそれぞれＢＤとＩＪの中点で、Ｐ・Ｋ・Ｑは一直線上にある。

ＡＰ＝２√２ｃｍ
ＥＧ＝ＢＤ＝４√２ｃｍでＥＱ＝√２ｃｍだから、ＱＧ＝３√２ｃｍ
△ＡＰＫ∽△ＧＱＫより、ＰＫ：ＫＱ＝２√２：３√２＝②：③
四角錘Ｋ―ＥＦＧＨの高さは、２√３×③/⑤＝６√３/５ｃｍ
したがって、その体積は、４×４×６√３/５÷３＝32√３/５ｃｍ³

大問６（整数）

（１）
長いすＡをｘ脚、長いすＢをｙ脚とすると、
２ｘ＋３ｙ＝20
係数の大きいｙで場合分けをする。
２ｘと20は偶数だから、３ｙは偶数でなければならない。
20÷３＝６…２
６までの偶数の個数なので、６÷２＝３個
（ｙ＝２、３、６はＯＫ。ｙ＝１、３、５はダメ）
長いすＢが０個の場合も許されるから、
３＋１＝４通り

（２）
２ｘ＋３ｙ＝127
127÷３＝42…１
２ｘは偶数、127は奇数だから、３ｙは奇数でなければならない。
ｙ＝１、３、５…
42以下（１～41）までの奇数の個数である。
（41＋１）÷２＝21通り

（３）
難問です:( ´ω` ):
数学上位層で暇を持て余した人たち向けの設問。

今まではｎがわかってａ通りを出した。
今度はａ通りからｎの最小値と最大値を求める。
つまり、処理過程を逆にさかのぼる。
ｎの値が偶数か奇数かで処理過程が異なるので、ｎの偶奇で場合分け。

◆ｎが偶数の場合
偶数である（１）ｎ＝20では、
20÷３＝６…２（３の倍数の個数）→６÷２＝３（６までの偶数の個数）→３＋１＝４（０を足す）

ただし、ｎ＝22を試してみると、
22÷３＝７…１→７までの偶数＝７以下の最大偶数６までの偶数の個数６÷２＝３→３＋１＝４
÷３した商が奇数の場合は、それに－１した偶数までの偶数の個数である。

これを逆の手順でさかのぼると、
最初はａ。
０を除外してａ－１。
（ａ－１）×２＝２ａ－２
÷３の商が偶数ならば２ａ－２だが、奇数ならば＋１して２ａ－１。
以下、さらに偶奇で場合分け。
【偶】（２ａ－２）×３＝６ａ－６
÷３した余りにも注目！３で割ったら余りは０～２。
ｎは偶数で６ａ－６は偶数だから、ｎ＝（６ａ－６）＋２＝６ａ－４もありえる！
ｎ＝６ａ－６、６ａ－４
【奇】（２ａ－１）×３＝６ａ－３
ｎは偶数で６ａ－３は奇数だから、余りで帳尻を合わせて、ｎ＝（６ａ－３）＋１＝６ａ－２

◆ｎが奇数の場合
奇数である（２）ｎ＝127では、
127÷３＝42…１（３の倍数の個数）→（41＋１）÷２＝21（42までの奇数の個数）
÷３の商が偶数なので42から－１した41までの奇数の個数である。

最初はａ。逆の手順では２倍して－１だから、２ａ－１。
ここで偶奇の場合分け。
【偶】（２ａ－１）＋１＝２ａ
２ａ×３＝６ａ
ｎは奇数で６ａは偶数だから、余りを使ってｎ＝６ａ＋１。
【奇】（２ａ－１）×３＝６ａ－３
ｎは奇数で６ａ－３は奇数。余りを使って（６ａ－３）＋２＝６ａ－１も可。
ｎ＝６ａ－３、６ａ－１

まとめると、６ａ－６、６ａ－４、６ａ－２、６ａ＋１、６ａ－３、６ａ－１。
最小の値…６ａ－６　最大の値…６ａ＋１