平均23.1点（前年比；＋1.5点）
最高点―50点、最低点―０点
問題はコチラ→ＰＤＦファイル
大問１（計算）
（１）
（－２）×４
＝－８
（２）
（－３）2＋８
＝９＋８
＝17
（３）
７ｘ－（６ｘ－１）
＝７ｘ－６ｘ＋１
＝ｘ＋１
（４）
９ａ3/５ｂ÷３ａ2/２ｂ2
＝６/５ａｂ
（５）
√12－√27
＝２√３－３√３
＝－√３
大問２（小問集合）
（１）
反比例は積ｘｙが比例定数で一定。
ｙ＝２×６÷４＝３
（２）
平行線をひいて、錯角でおろす。
ｘ＝46°
（３）
２ｘ2＋３ｘ－１＝０
解の公式を適用して、ｘ＝（－３±√17）/４
（４）
40匹のうち、印付きは11匹。
印付き全体は50匹なので池の魚は、
40×50/11＝2000/11≒181≒180匹
大問３（平面図形）
（１）
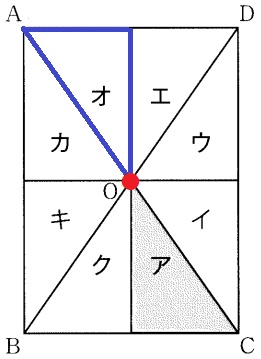
Ｏを中心としてアを回転移動させると、オと重なる（点対称）
オ
（２）
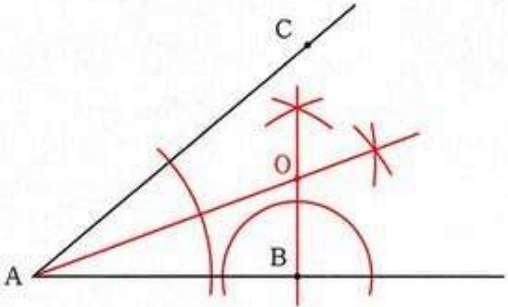
①Ｂで接する→Ｂを通るＡＢの垂線。
②ＡＢ、ＡＣに接する→Ｏは２つの半直線から等距離にある→∠ＣＡＢの二等分線。
これらの交点がＯ。
大問４（関数）
（１）
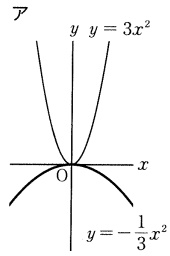
ａ＜０は上に凸のグラフ。
絶対値が小さいと、グラフの開きは大きくなる。
ア
（２）
平均の速さ⇒変化の割合
ｘ＝２→４の変化の割合を求めればいい。
ｙ＝ａｘ2において、ｘの値がｐ→ｑに増加するときの変化の割合はａ（ｐ＋ｑ）
３（２＋４）＝毎秒18ｍ
ボールが転がり始める時間＝０秒後
今度は、０→ｔの変化の割合が18になる。
３（０+ｔ）＝18
ｔ＝６
ア…18、イ…６
大問５（確率）
（１）
１の目は６個中３個。
確率は３/６＝１/２
（２）
答案では確率を求めるまでの過程を明らかにして説明する。
表で調べると、和が２の確率は９/36＝１/４
和が３の確率は12/36＝１/３
１/４＜１/３だから和が３の確率の方が高いので、Ｒの予想は正しくない。
大問６（方程式）
（１）
％は百分率。分母を100にすれば、分子が〇％に相当する。
ａ/400の分母分子を÷４する。
１/４ａ％
（２）
答案では連立方程式を立てて、過程も説明する。
ドリップバッグがｘ個、ティーバッグがｙ個。
ドリップ３個の袋…ｘ/３袋、ティー４個の袋…ｙ/４袋
袋の合計で等式。
ｘ/３＋ｙ/４＝100 …①
１個あたりドリップが70円、ティーが40円。
値段の合計で等式。
70ｘ＋40ｙ＝19000 …②
①×12で、４ｘ＋３ｙ＝1200 …③
②÷10で、７ｘ＋４ｙ＝1900 …④
④×３－③×４で、５ｘ＝900
ｘ＝180
③に代入、４×180＋３ｙ＝1200
ｙ＝160
ドリップバッグ…180個、ティーバッグ…160個
大問７（平面図形２）
（１）
△ＡＤＦ∽△ＣＥＦの証明。
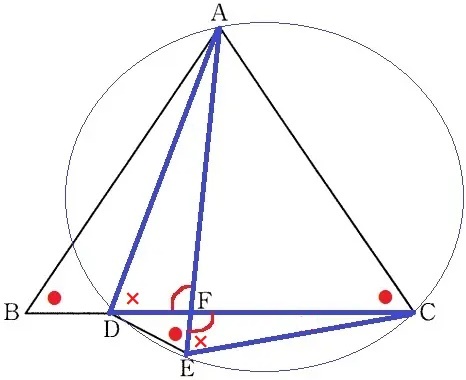
*円を描いたら楕円になってしまった(;^ω^)
対頂角で、∠ＡＦＤ＝∠ＣＦＥ
△ＡＢＣは二等辺三角形だから、∠ＡＢＤ＝∠ＡＣＤ（●）
折り返しで、∠ＡＢＤ＝∠ＡＥＤ（●）
２点Ｃ、ＥがＡＤについて同じ側にあり、∠ＡＣＤ＝∠ＡＥＤだから、
円周角の定理の逆より、４点Ａ、Ｃ、Ｄ、Ｅは同一円周上にある。
弧ＡＣの円周角より、∠ＡＤＦ＝∠ＣＥＦ（×）
２角が等しいから∽。
＠別解＠
弧ＤＥに対する円周角より、∠ＤＡＦ＝∠ＥＣＦを指摘しても良い。
（２）
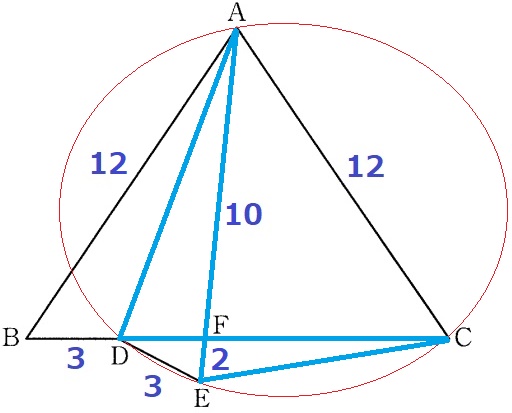
△ＡＢＣは二等辺→ＡＣ＝12ｃｍ
折り返しからＢＤ＝ＥＤ＝３ｃｍ、ＡＢ＝ＡＥ＝12ｃｍ
ＦＥ＝12－10＝２ｃｍ
前問の∽を利用しようとしても相似比がわからない…。
そこで、円に注目して△ＡＣＦ∽△ＤＥＦで捉える。
相似比は、△ＡＣＦ：△ＤＥＦ＝ＡＣ：ＤＥ＝④：①
ＣＦ＝２×④＝８ｃｍ
ＤＦ＝10×①/④＝５/２ｃｍ
よって、ＣＤ＝５/２＋８＝21/２ｃｍ
大問８（総合問題）
（１）
答案では評価３以上の相対度数をそれぞれ明らかにして説明する。
テントＡ…（330＋168＋72）÷800＝0.712…≒0.71
テントＢ…（345＋213＋92）÷1000＝0.65
テントＡの方が大きい。
（２）
山頂との標高差は、800－350＝450ｍ
100ｍで0.6℃下がるから、0.6×450/100＝2.7℃下がる。
山頂の気温は、20.8－2.7＝18.1℃
（３）
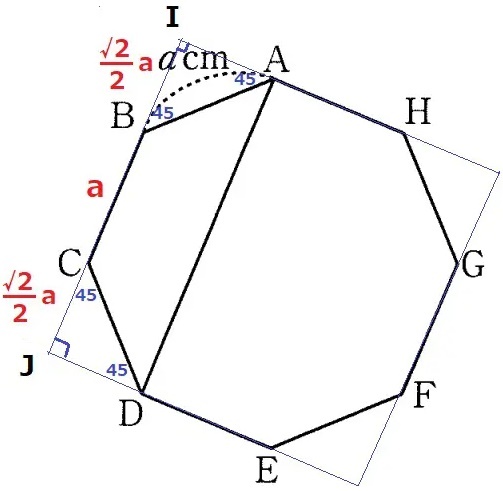
正八角形の１つの外角は、360÷８＝45°
上図のように正八角形を囲うと、外側は正方形で四隅は直角二等辺。
対角線ＡＤは正方形の１辺ＩＪと等しい。
直角二等辺の辺の比は１：１：√２→ＩＢ＝ＣＪ＝ａ×１/√２＝√２/２ａ
ＩＪ＝ａ＋√２/２ａ×２＝ａ＋√２ａ＝（１＋√２）ａｃｍ
大問１
配点５点。全問死守。
大問２
いずれも基本問題。
大問３
ここも典型題。
大問４
（２）差がつく。
平均の速さは鹿児島大問４で出題された（正答率22.4％）
ｘ＝２、４であるグラフ上の２点を結んだ一次関数の傾きに相当する。
アとイも同じ要領で解ける。
大問５
（２）特殊なサイコロゆえ、表で調べる。
確率が最も高いのは３と指摘すればいい。
大問６
（１）基礎的な割合の問題だが、他県の類題では正答率が軒並み低い。。20％はなさそう。
（２）問題文の文字数は多いが、設問は標準レベル。
大問７
（１）対頂角はわかるが、もう１つの等角を指摘できるか。
図形の特徴は二等辺と折り返し。等角を手掛かりに円を見つける。
円周角の定理の逆の言い回しはおさえておきたい。
（２）前問の円が見つけられることが前提。
まずは求められる長さを求めておく。ＣＤ＝ＣＦ＋ＦＤ→別の∽に切り替える。
大問８
（２）算数の範囲で解ける。間違いたくない。
（３）経験の差が出やすいか。外角45°を活用する。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント