2020年度　栃木県公立高校入試過去問【数学】解説

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）　98.3％
（－18）÷２＝－９

（２）　92.7％
４（ｘ＋ｙ）－３（２ｘ－ｙ）
＝４ｘ＋４ｙ－６ｘ＋３ｙ
＝－２ｘ＋７ｙ

（３）　76.4％
１/６ａ²×（－４ａｂ²）
＝－２/３ａ³ｂ²

（４）　79.7％
５√６×√３
＝５√18＝15√２

（５）　93.0％
（ｘ＋８）（ｘ－８）
＝ｘ²－64

（６）　81.0％
解が７→ｘ＝７を代入。
２×７－ａ＝－７＋５
ａ＝16

（７）　74.1％
割り算の式で整理するとわかりやすい。
100÷６＝ｘ…ｙ
６ｘ＋ｙ＝100
*公式解答は100－６ｘ＝ｙだが同じ。

（８）　84.5％

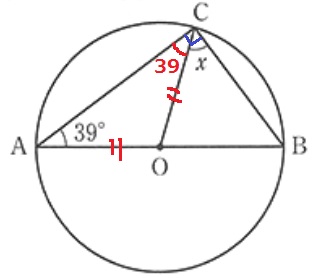
半円の弧に対する円周角は直角→∠ＡＣＢ＝90°
半径より△ＡＣＯは二等辺→∠ＡＣＯ＝39°
∠ｘ＝90－39＝51°

（９）　64.1％
ｘ²－９ｘ
＝ｘ（ｘ－９）＝０
ｘ＝０、９

（10）　72.4％
14個の玉から、赤と青の12個の玉を取り出せばいい。
12/14＝６/７

（11）　82.4％
半径３ｃｍ、高さ６ｃｍの円柱。
３×３×π×６＝54πｃｍ³

（12）　83.2％
対応する辺を取り違えないように。

錯角で等しい角に印をしてみよう。
４とｘ、５と２が対応する。
ｘ＝４×２/５＝８/５ｃｍ

（13）　74.7％
右下なので、傾きａは負。
切片ｂはｙ軸との交点→正。
ウ

（14）　90.1％
100個の中に２個の不良品。
この割合は母集団でも同じだとみなす。
4500×２/100＝90個

大問２（小問集合２）

（１）　62.4％
Ａを回転の中心として、Ｃを『時計回りに25°』回転させる。

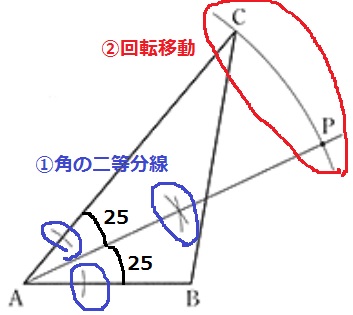
使うのは∠Ａ＝50°のみ。
①角の二等分線で25°を作成。
②ＡからＣの距離をとり、これを①の線上に移す。
その交点が点Ｐとなる。

（２）　71.5％（部分正答含む－85.3％）
ｂはａの６日後。
①…６

ｃはａの12日後。
②…12

ｂ²－ａｃ
＝（ａ＋６）²－ａ（ａ＋12）
＝ａ²＋12ａ＋36－ａ²－12ａ
＝36
結果が変数ａを含まない、定数項36。
よって、つねに36となる。
③…36

（３）　32.1％！
各々のｙ座標を調べる。

ＡＢ＝ａ＋４
ＣＤ＝16ａ＋１
７（ａ＋４）＝16ａ＋１
ａ＝３

大問３（方程式・標本調査）

（１）　47.5％（部分正答含む－79.8％）
途中式も記述する。
昨年のＡ中をｘ人、Ｂ中をｙ人とする。
１文目から、ｘ＋ｙ＝1225…①
２文目から昨年度からの増減の和で、合計の変化を等式であらわす。
〔Ａの４％－Ｂの２％＝４人〕
0.04ｘ－0.02ｙ＝４…②
これを100倍して、４ｘ－２ｙ＝400
さらに÷２して、２ｘ－ｙ＝200…③
①＋③
ｘ＋ｙ＝1225
＋)２ｘ－ｙ＝200
３ｘ　　＝1425
ｘ＝475
①に代入。ｙ＝1225－475＝750
Ａ中…475人、Ｂ中…750人
正確な処理能力が問われる。

（２）①　25.0％！
誤差の範囲。
小数第２位以下が切り捨てられている。
四捨五入を思い出そう！ポイントは”最後が５”。
28.65以上28.75未満
→28.65≦ａ＜28.75

②　66.0％
最頻値（モード）は、最もあらわれている値。
解答する際は階級値で答える。
すなわち、30と35の平均である32.5℃。

③　31.2％！（部分正答含む－42.9％）
表２より、最大値は34℃以上36℃未満の範囲にある。

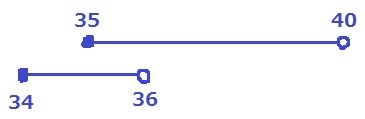
表１と合わせると、重なるところは35℃以上36℃未満。
最大値はかかる範囲に含まれる。

＠公式解答より引用＠
表１において35.0℃以上40.0℃未満の日が１日あり、
表２において36.0℃以上の日がないから。

大問４（図形）

（１）　24.5％！（部分正答含む－63.4％）
△ＡＤＦ≡△ＢＦＥの証明。

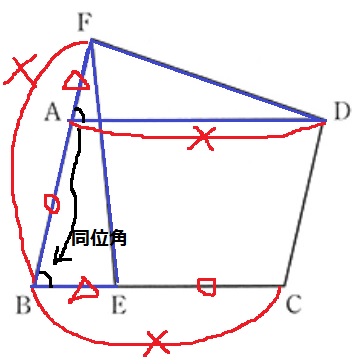
等辺をきっちりおさえよう。
平行四辺形の対辺と仮定から、ＡＤ＝ＢＦ（×）
×－〇＝△より、ＡＦ＝ＢＥ
同位角より、∠ＤＡＦ＝∠ＦＢＥ
以上から、２辺とあいだの角が等しく合同。

（２）①　52.0％
１辺２ｃｍの正三角形の面積。
半分にわって１：２：√３より、高さは√３ｃｍ。
２×√３÷２＝√３ｃｍ²

②　10.1％！
切断面を求積する。
取っ掛かりをつかむために、ひとまず辺の長さを調査する。

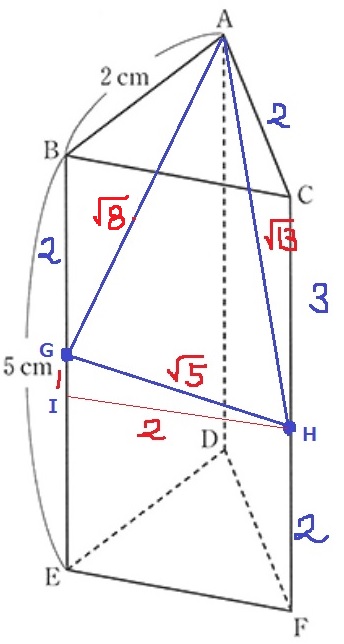
三平方を器用に使う。
ＧＨの長さは、うえのように△ＧＨＩで三平方を適用する。

ＡＧ＝√８の形にすると、あることが見えてくる…。
（√８）²＋（√５）²＝（√13）²
三平方の定理の逆から、△ＡＧＨは∠ＡＧＨ＝90°とする直角三角形。
√５×√８÷２＝√10ｃｍ²

大問５（数量変化）

（１）　72.2％
水泳300ｍにおいて、時間の比は、
明：拓也＝４：６＝２：３
速さは時間の逆比。
明：拓也＝３：２
よって、明の速さは拓也の３/２倍。

（２）　36.6％
明の自転車は12分で6000ｍを完走する。
6000÷12＝分速500ｍ
拓也がＡ地点に着いた６分後に、明はすでに２分間自転車で走っている。
500×２＝1000ｍ

（３）　34.2％（部分正答含む－52.7％）
記述式。
明は長距離走を10分間で2100ｍ走る。
傾きは、2100÷10＝210
ｙ＝ａｘ＋ｂにおいて、ａ＝210、（16、6300）を通る直線の式を求める。
6300＝210×16＋ｂ
ｂ＝2940
ｙ＝210ｘ＋2940

（４）　11.2％！
グラフに書き込みながら整理しよう。

明より３分遅れたので、拓也は29分にゴールする。
その10分前にＢ地点を通過。
パンクした2700ｍ～Ｂ地点までの3600ｍを分速600ｍで走るので、
3600÷600＝６分間走ったことになる。
つまり、パンクから復帰したのはスタートから13分後。

今度はＡ地点から攻める。
パンク前の拓也の自転車は明と同じ速度→（２）より分速500ｍ
（2700－300）÷500＝4.8分
パンクしたのはスタートから、4.8＋６＝10.8分後
よって、パンク修理にかかった時間は、13－10.8＝2.2分＝２分12秒

大問６（規則）

（１）　73.5％
『白→灰→黒→…』で１ループ。
４個目の灰色がでてくるのは３ループ＋２。
３×３＋２＝11番目

（２）　77.0％
20÷３＝６…２
６ループ＋２
余り２は〔白・灰〕で、黒を含まず。
よって、黒は６個。

（３）　19.9％！（部分正答含む－32.0％）
記述式。
半径＝ｎとして、最も外側の輪の面積をｎで表す。
〔半径ｎの円の面積〕－〔半径ｎ－１の円の面積〕
πｎ²－π（ｎ－１）²
＝π｛ｎ²－（ｎ－１）²｝
＝π（２ｎ－１）＝77π

２ｎ－１＝77
ｎ＝39

（４）①　1.1％!!（部分正答含む－3.8％）
難しい。

半径ａで５等分された外側のピースの周と、
半径ｂで９等分された外側のピースの周が等しくなった。
前問と同じように周りの長さを計算する。
中心角は72°：40°＝９：５（５等分：９等分の逆比）
弧の長さは中心角に比例するので、中心角の計算は⑨：⑤で算出。
また、直線部分の２はどちらも同じなので、あらかじめ両者から差し引いておく。
｛２πａ＋２π（ａ－１）｝×⑨
＝（４πａ－２π）×⑨
＝36πａ－18π

｛２πｂ＋２π（ｂ－１）｝×⑤
＝（４πｂ－２π）×⑤
＝20πｂ－10π

36πａ－18π＝20πｂ－10π　←π消去
36ａ－18＝20ｂ－10
20ｂ＝36ａ－８
ｂ＝（９ａ－２）/５

②
前問の答えを利用する。
ｂ＝（９ａ－２）/５　←両辺を５倍
５ｂ＝９ａ－２

５等分されたピースと９等分されたピースの周の長さが等しくなるとき、
９等分されたピースの方が中心角が小さいので、半径を長くとらなければならない。
すなわち、ｂ＞ａ。
同じ色は３の倍数個先なので、ａから３の倍数個足せばｂとなる。
ｂの値を最小にするから、ａに３・６・９・12…を足して順に確かめる。
◆ｂ＝ａ＋３のとき
５（ａ＋３）＝９ａ－２
４ａ＝17
ａ＝17/４　…ａは自然数なので×

◆ｂ＝ａ＋６のとき
５（ａ＋６）＝９ａ－２
４ａ＝32
ａ＝８　…〇
よって、ａ＝８