問題はコチラ→ＰＤＦファイル
60分100点満点
大問１（小問集合）
（１）
（ｘ＋３ｙ）：（４ｘ－２ｙ）＝３：５ …①
３ｘ－５ｙ＝12 …②
①内項と外項の積より、
３（４ｘ－２ｙ）＝５（ｘ＋３ｙ）
12ｘ－６ｙ＝５ｘ＋15ｙ
７ｘ＝21ｙ
ｘ＝３ｙ …③
②に代入。
３×３ｙ－５ｙ＝12
４ｙ＝12
ｙ＝３
③に代入。ｘ＝３×３＝９
ｘ＝９、ｙ＝３
（２）
高校レベルに突っ込んでる(;’∀’)
対称式を使います。
ａ＋ｂ＝（√３＋√15）＋（√３－√15）＝２√３
ａｂ＝（√３＋√15）（√３－√15）＝３2－152＝－12
式の変換ではａ＋ｂとａｂだけの形に持っていく。
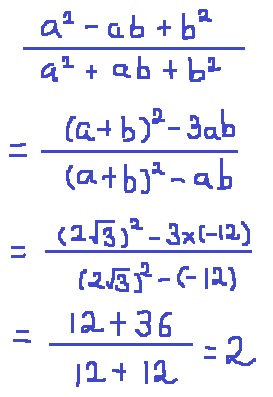
*ａ2－ａｂ＋ｂ2＝ａ2＋２ａｂ＋ｂ2－３ａｂ＝（ａ＋ｂ）2－３ａｂ
（３）
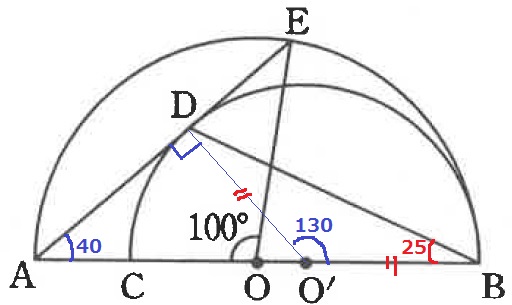
△ＡＥＯは半径より二等辺→∠ＥＡＯ＝（180－100）÷２＝40°
Ｏ’Ｄに補助線。
半径と接線は直交するので、∠ＡＤＯ’＝90°
△ＡＤＯ’の外角定理から、∠ＤＯ’Ｂ＝40＋90＝130°
△Ｏ’ＤＢも半径より二等辺→∠ＤＢＯ’＝（180－130）÷２＝25°
△ＡＤＢで外角定理→∠ＢＤＥ＝40＋25＝65°
（４）
（ｐ、ｑ）＝（19、１）（18、２）（17、３）…（11、９）の９通り。
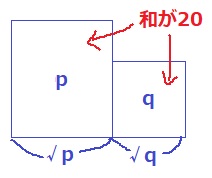
１辺が√ｐと√ｑの正方形があり、２つの面積の合計は20で一定。
このとき、√ｐ＋√ｑの長さがMaxになるのはどういうときだろう？(‘Д’)
…勘のイイ人はすぐ思いついてしまう(^^;
極端なケースを想定する。
条件はｑ＞０だが、仮にｑ＝０にしてｐの面積を20とすると、√ｐ＝√20
ｐ＞ｑを無視して、仮にｐ＝ｑ＝10とすると、√ｐ＋√ｑ＝√10＋√10＝２√10＝√40
√20＜√40だから、ｐとｑの面積が等しい場合に近いほど、長さの和が長くなるはず！
ということは、√ｐ＋√ｑにおいて最も値が大きいのは√11＋√９、
２番目は√12＋√８、３番目は√13＋√７となる。
（ｐ、ｑ）＝（13、７）
（５）
難しい(´ﾟωﾟ`;)
４ｍ3＋ｎ2＝2020
ｎ2＝2020－４ｍ3
ｎ2＝４（505－ｍ3）
左辺のｎ2が平方数。
４も平方数なので、505－ｍ3も平方数になるはず。
３乗が曲者だが…８×８×８＝512なのでｍは７以下。
ｍ＝１⇒505－１＝504×
ｍ＝２⇒505－８＝497×
ｍ＝３⇒505－27＝478×
ｍ＝４⇒505－64＝441＝21×21〇
ｍ＝５⇒505－125＝380×
ｍ＝６⇒505－216＝289＝17×17〇
ｍ＝７⇒505－343＝162×
*20までの平方数は暗記しておくのがベター。
ｍ、ｎは２組しかないとあるので、もう１個がでれば終了。
ｎの値は素因数に注目。（４＝２×２の２だけを抜き出す）
ｍ＝４のとき、ｎ＝２×21＝42
ｍ＝６のとき、ｎ＝２×17＝34
（ｍ、ｎ）＝（４、42）（６、34）
他に良い解法を編み出した方は、ぜひお問い合わせかコメント欄でお知らせ願いますm(＿)m
大問２（関数）
（１）
Ａはｙ＝ａｘ2とｙ＝ａ/ｘの交点。
ａｘ2＝ａ/ｘ ←両辺をｘ倍
ａｘ3＝ａ ←両辺を÷ａ
ｘ3＝１
高２で虚数ｉを用いて三乗根ω（オメガ）を習いますが、
中学の範囲では□×□×□＝１にあてはまる数は１しかないと感覚で答えるしかないと思う。
ｘ＝１
ｙ＝ａｘ2に代入して、A（１、ａ）
（２）
直線ＰＱの式をｙ＝ａｘ＋ｂとする。
ＰとＱはｙ＝ａｘ2とｙ＝ａｘ＋ｂの交点。
ａｘ2＝ａｘ＋ｂ
ａｘ2－ａｘ－ｂ＝０
ここで解の公式を適用。
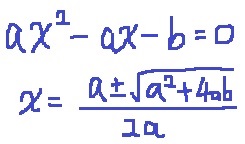
求めたいのはｐ＋ｑの値。ｐは負、ｑは正だから…
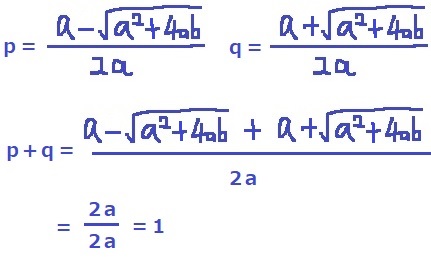
（３）
ｐとｑの座標の距離はｑ－ｐ。
Ｒのｘ座標はｐとｑの中点だから、
ｐから（ｑ－ｐ）/２を足せばいい。
ｐ＋（ｑ－ｐ）/２
＝（２ｐ＋ｑ－ｐ）/２
＝（ｐ＋ｑ）/２＝１/２
これをｙ＝ａ/ｘに代入。
Ｒのｙ座標は、ｙ＝ａ÷１/２＝２ａ
Ｒ（１/２、２ａ）
（４）
ｂがわかる。
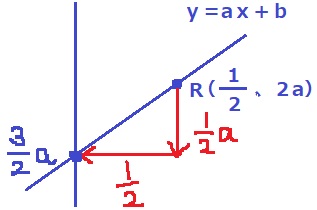
ｙ＝ａｘ＋ｂの傾きａは右に１いくと上にａあがる。
Ｒから切片に移動すると、下に１/２ａ、左に１/２。
ここから切片は、２ａ－１/２ａ＝３/２ａ
ＰとＱはｙ＝ａｘ2とｙ＝ａｘ＋３/２ａの交点だから、
ａｘ2＝ａｘ＋３/２ａ
ｘ2－ｘ－３/２＝０
２ｘ2－２ｘ－３＝０
解の公式を適用、ｂ＝２ｂ’が使える。
ｘ＝（１±√７）/２
ｐ＜０、ｑ＞０だから、ｐ＝（１－√７）/２、ｑ＝（１＋√７）/２
（５）
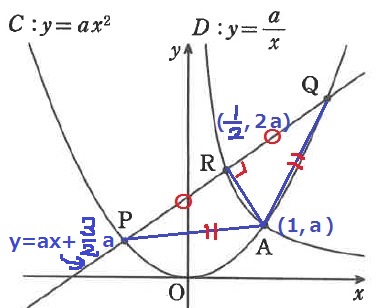
ＡＰ＝ＡＱなので、△ＡＰＱは二等辺三角形。
頂角Ａから底辺ＰＱの中点にあるＲを結ぶとＡＲ⊥ＰＱ。
ＡＲの傾きは、（ａ－２ａ）/（１－１/２）＝－２ａ
２本の直線が直交するとき、傾きの積は－１。
ＰＱの傾き…－１÷－２ａ＝１/（２ａ） ←ａは分母にある
これがｙ＝ａｘ＋３/２ａの傾きａと同じ。
ａ＝１/（２ａ） ←両辺を２ａ倍
２ａ2＝１
ａ2＝１/２
ａ＞０より、ａ＝√２/２
大問３（確率）
（１）
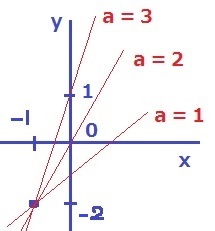
ａが３以上になって、切片ｂが１以上となる。切片ｂは６まで許容。
（ａ、ｂ）＝（３、１）（４、２）（５、３）（６、４）
４通り
（２）
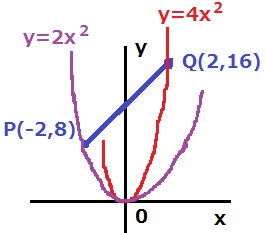
直線ＰＱではなく線分ＰＱに注意！(`ω´)
ｙ＝２ｘ2で線分Ｐに触れる。
ということは、これより開きが大きくなるｙ＝ｘ2では共有点なし。
ｃ＝２～６→５通り
（３）
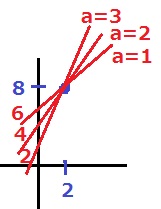
１≦ｂ≦６より、
（ａ、ｂ）＝（１、６）（２、４）（３、２）で３通り。
放物線はｙ＝２ｘ2しかない→ｃ＝２で１通り。
全部で６×６×６通りなので、
（３×１）/（６×６×６）＝１/72
（４）
ｃに１～６を代入して、ｘ＝２のときのｙ座標で場合分け。
◆ｃ＝１、ｙ＝４
（ａ、ｂ）＝（１、２）の１通り。
◆ｃ＝２、ｙ＝８
前問から３通り。
◆ｃ＝３、ｙ＝12
（３、６）（４、４）（５、２）の３通り。
◆ｃ＝４、ｙ＝16
（５、６）（６、４）の２通り。
◆ｃ＝５、ｙ＝20
ｙ＝６ｘ＋６にしてｘ＝２を代入すると18。
ｙの最大値は18なので無い。
◆ｃ＝６、ｙ＝24
同様に無い。
計９通り。
９/（６×６×６）＝１/24
（５）
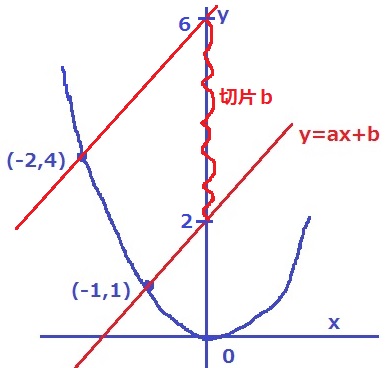
ｙ＝ａｘ＋ｂは右上に伸びるので、ｘ＜０の格子点に注目する。
（－１、１）か（－２、４）しかない。
なぜなら、切片ｂは１～６の範囲で、（－３、９）だと６を超えてしまうから。
まず、（－１、１）を基準に検証。
◆傾き１
（ａ、ｂ）＝（１、２）
傾き１は45度線で格子点を通る。〇
◆傾き２
（ａ、ｂ）＝（２、３）
ｙ＝ｘ2とｙ＝２ｘ＋３の交点を求める。
ｘ2＝２ｘ＋３
ｘ2－２ｘ－３＝（ｘ＋１）（ｘ－３）＝０
ｘ＝－１、３でＯＫ。〇
◆傾き３
（ａ、ｂ）＝（３、４）
ｘ2－３ｘ－４＝（ｘ＋１）（ｘ－４）＝０ＯＫ
◆傾き４
（ａ、ｂ）＝（４、５）
ｘ2－４ｘ－５＝（ｘ＋１）（ｘ－５）＝０ＯＫ
◆傾き５
ｘ2－５ｘ－６（ｘ＋１）（ｘ－６）＝０ＯＫ
次に、（－２、４）を基準とする。
傾き１で（１、６）しかない。
ｙ＝ｘ2とｙ＝ｘ＋６の交点座標は…
ｘ2－ｘ－６＝（ｘ＋２）（ｘ－３）＝０ＯＫ
計６通り
大問４（平面図形）
（１）
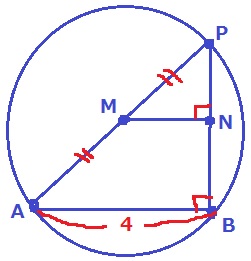
↑ＰＡが直径のとき。Ｍが中心Ｏ。
半円の弧に対する円周角は直角なので、∠ＡＢＰ＝90°
△ＰＭＮ∽△ＰＡＢより、ＭＮ＝４÷２＝２
（２）
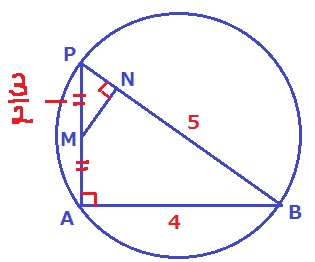
半円の弧に対する円周角で∠ＰＡＢ＝90°
△ＰＢＡは３：４：５の直角三角形。
面積は３×４÷２＝６
ＭＰ＝３÷２＝３/２
△ＰＢＡと△ＰＭＮの面積比を求める。
面背比は辺の比の２乗。
５2：（３/２）2
＝25：９/４＝100：９
よって、△ＰＭＮの面積は、６×９/100＝27/50
（３）
エエエ:(っ`ω´c):
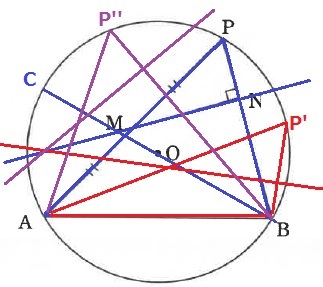
適当に調べてみると左のところに集まっている・・。
ＡとＣのあいだっぽい。
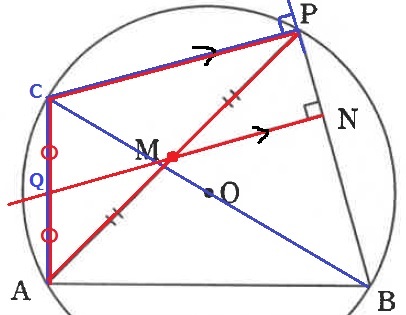
ＢＣは直径。これに対する円周角である∠ＢＰＣ＝90°
同位角が等しく、ＣＰ//ＭＮ。
ＭＮとＡＣの交点をＱとする。
ＣＰ//ＭＮから２角が等しく、△ＡＣＰ∽△ＡＱＭ
ＡＱ：ＱＣ＝ＡＭ：ＭＰ＝１：１
定点ＱはＡＣの中点にある。
（１）（２）の図から直線ＭＮを描いてＱの位置を探るのが良かったかな？
大問５（空間図形）
（１）
問題文に数字が２つしかない。。
球の半径が１なので、球と正四角錘が接するポイントを探す。
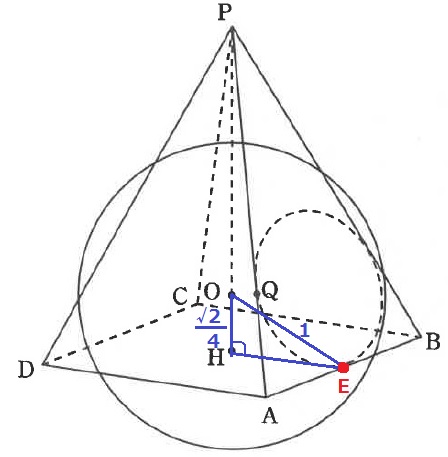
ＡＢの中点をＥとする。Ｅが接点！
△ＯＨＥで三平方。
ＨＥ2＝１2－（√２/４）2
＝１－１/８＝７/８
ＨＥ＞０より、ＨＥ＝√14/４
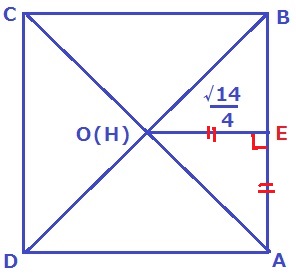
△ＨＥＡは直角二等辺だから。ＡＨ＝√14/４×√２＝√７/２
（２）
ＯＨ＝√２/４、ＡＨ＝√７/２
△ＯＡＨで三平方。
ＯＡ2＝（√２/４）2＋（√７/２）2＝15/８
ＯＡ＞０で、ＯＡ＝√30/４
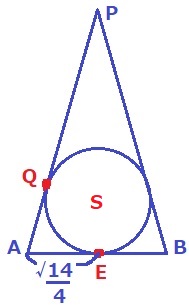
前問のＥを使う。
球面ＳとＰＡの接点がＱ。
Ｅも球面上にあるＡＢとの接点。
△ＡＰＢで球面ＳはＡＰ上でＱと、ＡＢ上でＥと接する。
そして、円外の点から接点までの接線の長さは等しい。
ＱＡ＝ＥＡ＝√14/４
（３）
（２）と同じ、２本の線分の長さを求めるが、
わざわざｘ、ｙに置き換えているということは連立を組めということ。
ＰＯとＰＱを１辺とする三角形で相似関係を見つける。
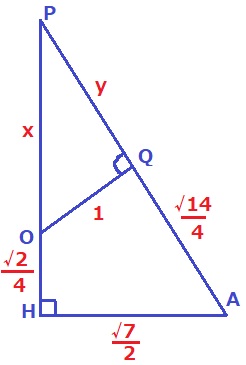
ズバリ、△ＰＡＨ∽△ＰＯＱ。
ＰＯ：ＯＱ＝ＰＡ：ＡＨから、
√７/２ｘ＝ｙ＋√14/４ …①
ＰＱ：ＱＯ＝ＰＨ：ＨＡから、
√７/２ｙ＝ｘ＋√２/４ …②
これを解けばいいが、計算処理がツライ(;´Д｀)
以下、代入法。
(*‘ω‘ *)ｷｯﾂｰ
ｘ＝３√２/２、ｙ＝√14/２
（４）
ＰＡ＝ＰＱ＋ＱＡ＝√14/２＋√14/４＝３√14/４
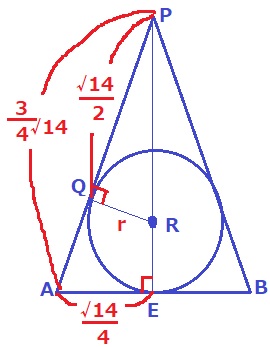
球面Ｓの中心をＲとする。
△ＡＰＥで三平方→ＰＥ＝√７
△ＡＰＥ∽△ＲＰＱよりＱＲの長さは、
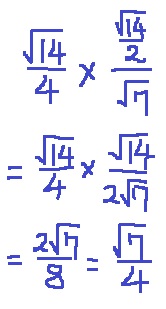
ｒ＝√７/４
＠データ＠
英国数理社各100点の500点満点
合格最高点348点、合格最低点257点
総合平均点（合格者）293点（受験者）239点
６割↑は欲しい。
公立高校入試解説ページに戻る
コメント