2014年度　千葉県公立高校入試【後期】数学解説

問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）－３＋８＝５

（２）７－（－６）²÷９
＝７－３６÷９
＝７－４
＝３

（３）６（１/３ａ－１/２ｂ）－２ａ＋ｂ
＝２ａ－３ｂ－２ａ＋ｂ
＝－２ｂ

（４）√８×（－√５）
＝－√４０
＝－２√１０

（５）ｘ＝－２のとき、ｘ²＋１０/ｘの値を求めなさい。
素直に代入。
（－２）²＋１０÷（－２）＝４－５＝－１

（６）ｘ²－ｘ－１２を因数分解しなさい。
（ｘ－４）（ｘ＋３）
*普段より簡単な問いなので、オールクリアを目指したい。

大問２（小問集合）

（１）エ
*絶対値の定義を知っていれば容易。
－４、－３、－２、－１、０、１、２、３、４。
絶対値とは、数直線上で原点０からの距離。
整数なので０や負の数を含む。

（２）
定価の４割引ということは、定価の６割で購入して６００円支払った。
よって、６００×１０/６=１０００

（３）
いびつな図形のように思えるが、立体図形を頭の中で組み立ててみると、
底辺が真ん中の台形、高さが３ｃｍの四角錐とわかる。台形の上底と下底を知りたい。

一番上の直角三角形は３：４：５で上底は４。
下底を求めたい。√１３があるが意味無し。
なぜか１つだけ４５°という角度が示されていることに注目！

下の点をＡ、そこから上に垂線を引き交点をＢ、右端をＣとおく。
△ＡＢＣは直角二等辺三角形 。
よって、２＝ＡＢ（●）＝ＢＣ（●）
○＝４－●＝４－２＝２・・台形の下底
よって、（４＋２）×２×１/２×３×１/３＝６ｃｍ³

（４）
どの辺が等しくなるか、３パターンある。
＠ＡＰ＝ＡＢ＠
試しに書いてみる。サイコロの目は１～６なので、
Ｐは（１、１）～（６、６）のどれか。よって、なし。
＠ＡＢ＝ＢＰ＠
同様になし。
＠ＡＢ＝ＡＰ＠
これしかない。
つまり、点Ｐが点Ａと点Ｂから等しい距離にある。
等しい距離といえば垂直二等分線。

ＡＢの中点Ｍの座標は、（１＋７）÷２、（８＋２）÷２＝５　Ｍ（４，５）
ＡＢの傾きは、７右いって７下がる→傾き＝－１
ということは、垂直二等分線の傾き＝１　*直角に交わる線分の傾きの積は－１

Ｍ（４，５）で傾きが１。数値を１個ずつずらしていけばＯＫ．
（大、小）＝（１，２）（２，３）（３，４）（４，５）（５，６）
ただし、Ｍ（４，５）はＭが直線ＡＢ上にくるので三角形にならない。
だから残りの４通りが答え。　確率は４/３６＝１/９

（５）
前期の作図と比べれば楽勝。
ただ、ひし形の性質を思い出して最初の突破口を見出せるかが正否の分かれ目。

ひし形の対角線は各々の角を２等分する。
ということは、点Ｃの反対側にくる点Ｐは、点Ｃの角の２等分線上にある。

初期状態。

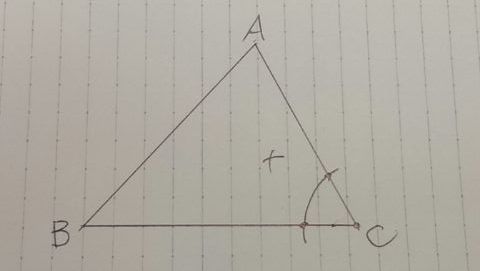
∠Ｃの二等分線の構え。

これだけでＰがでてしまう。
ひし形の対角線は各々の中点で交わり、かつ直角に交わるので、
ＰＣの垂直二等分線をひけばＱ、Ｒもでて終わり。

＠別解＠

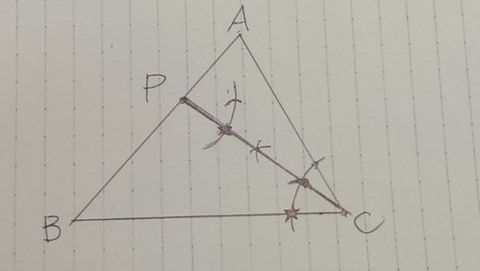
ひし形は平行四辺形の性質を併せ持つ。
そこでＰを通るＢＣに平行な線分をひきたい。
錯角を利用して∠ＢＣＰを∠Ｐに移す。
∠Ｃ→∠Ｐへひょこ、★から長さを頂いて上の★からひょこ。

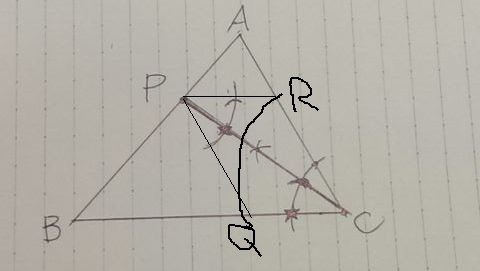
Ｒ完成。
ひし形は全ての辺の長さが等しいので、ＣＲをとって辺ＢＣに移せばＱ。
写真では平行四辺形になってしまいましたが・・・正確にやればひし形になります。

大問３（関数）

（１）
仮定から、Ａのｘ座標は４とわかっているので、ｙ＝２ｘ－６にあてはめる。
ｙ＝２×４－６＝２　　Ａ（４，２）
これをｙ＝ａｘ²にあてはめ。
２＝４²a
１６ａ＝２
ａ＝１/８

（２）
グラフ上での面積比を求める問題。
複雑で面倒くさいが地道に求める。

仮定からＢのｘ座標が－２。　（１）よりｙ＝１/８ｘ²に代入。
Ｂ（－２，１/２）

ＢＤはＯＡと平行。平行は傾きが一緒。
ＯＡの傾きは、右に４いって上に２あがるので１/２。
ＢＤの直線の式を求める。
１/２＝－２×１/２＋ｂ
ｂ＝３/２
ＢＤ：ｙ＝１/２ｘ＋３/２
これとｙ＝２ｘ－６との交点を求めてＤ（５、４）

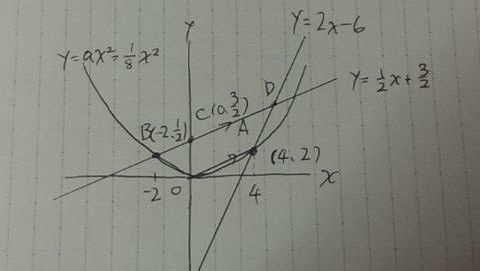
いろいろやり方があると思うが、ここでは王道の等積変形を用いる。
四角形ＯＡＤＣを、y軸に接する三角形に変形させる。
ＯＤに線分を引き、それと平行で点Ａを通る直線をひく。

四角形OADCの面積＝三角形A’DCの面積

ＯＤの傾きは右５上４→傾き４/５
点Ａ（４，２）だから、
ＡＡ’：２＝４×４/５＋ｂ
ｂ＝－６/５
ＡＡ’：ｙ＝４/５ｘ－６/５
Ａ’の座標は（０、－６/５）

△ＯＣＢと△Ａ’ＣＤには共通辺がないので、底辺×高さが面積比になる。
△ＯＣＢ：△Ａ’ＣＤ
＝３/２×２：(３/２＋６/５)×５
＝３：２７/２
＝６：２７
＝２：９
*処理がめんどいので、後回しにしても可。

＠別解＠

四角形ＢＯＡＤは台形。
三角形ＯＣＢと四角形ＯＡＤＣの面積比は、底辺の比からＢＣ：ＣＤ＋ＯＡとなる。
三平方の定理から、ＢＣ＝√４＋√１＝√５
ＣＤ＝√２５＋√(２５/４)＝５/２ √５
ＯＡ＝√１６＋√４＝２√５
ＢＣ：ＣＤ＋ＯＡ
＝√５：５/２ √５＋２√５
＝√５：９/２ √５　←√５でわる。
＝１：９/２
＝２：９

大問４（平面図形）

（１）
（a）…△ＯACとあるので、それを凝視。OAは半径。よってOC。　ａ…ウ
（ｂ）…【２】【３】より、△ＯＡＣは直角二等辺三角形なので、∠ＯＣＡ＝４５°　ｂ…エ

（ｃ）
前期と同様、昨年と比べれば簡単。
辺の情報が少ないので、角度で攻める。
【１】から共通角があげられているので、残りの２つの角に的をしぼる。
誘導のところで∠ＯＣＡ＝４５°とわかったので、△ＦＯＥの中で４５°になる角を探す。

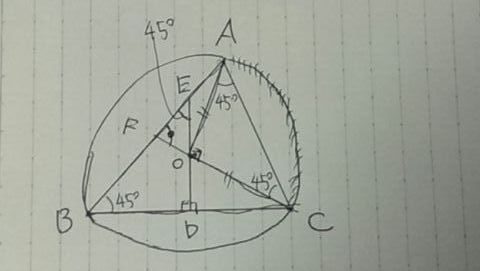
図形が円に囲まれている→円周角定理の活用
弧ＡＣの円周角∠ＡＢＣ＝４５°
△ＢＤＥにおいて、残りの角である∠ＤＥＦ＝４５°
以上から、２角が等しくなるので△ＦＯＥ∽△ＦＡＣ

以下、模範解答。
～～引用はじめ～～
△ＢＤＥにおいて、円周角の定理より、
∠ＡＢＣ＝１/２∠ＡＯＣ＝４５°　　　・・・【５】
仮定より、　　　∠ＢＤＥ＝９０°　　　・・・【６】
【５】、【６】より、　　∠ＤＥＢ＝４５°　・・・【７】
【４】、【７】より、　　∠ＦＥＯ＝∠ＦＣＡ　　・・・【８】
【１】、【８】より、２角が、それぞれ等しいので、
△ＦＯＥ∽△ＦＡＣ
～～引用おわり～～

（２）やや難問

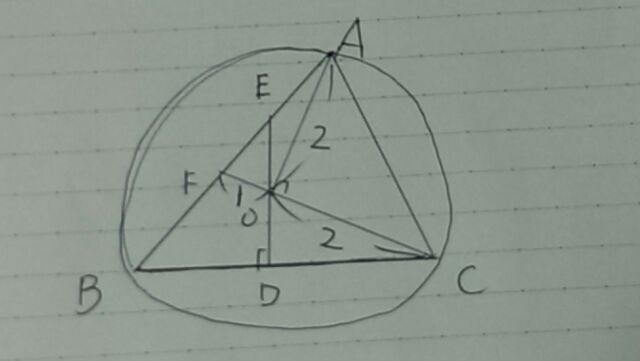
初期状態。
△ＦＯＥ内で底辺×高さ÷２をするより、
底辺と高さが既にわかっている三角形から相似で求めたほうが良さげ。
そこで、前問の△ＦＯＥ∽△ＦＡＣを利用する。
△ＡＦＯ内で三平方→ＦＡ＝√５

対応する辺がＦＯ：ＦＡとなり、△ＦＯＥ：△ＦＡＣ＝ＦＯ：ＦＡ＝ １：√５

ＦＣが３ｃｍ、先ほどの相似比をつかってＥＦの長さを出す。
３×１/√５＝３√５/５

△ＡＦＯの面積は、１×２÷２＝１ｃｍ²
同じ高さの三角形は底辺の長さの比が面積比になるので、
△ＡＦＯ：△ＦＯＥ＝√５：３/５ √５
よって、△ＦＯＥ＝１×(３√５/√５) / √５＝３/５ｃｍ²
上の写真の右のように、分子・分母を√５倍すれば分母を払える。

大問５（規則）

（１）

図３を見れば明らか。
４枚重なっている部分は、ど真ん中の小さな正方形。よって１ｃｍ²。

（２）
ア・・図２を見れば明らか。４×４－３×３＝７ｃｍ²
”それぞれ”なので１４ｃｍ²にしないこと！

イ＆ウ・・図３を駆使すれば、なんとかなる問題。

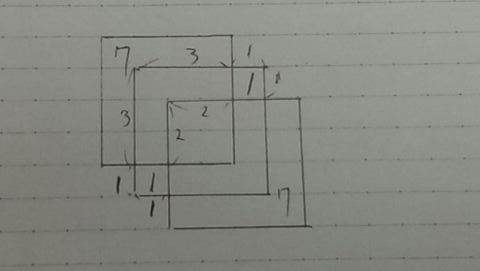
イ・・７ｃｍ²     ウ・・１＋１＝２ｃｍ²

エ・・規則性を見つける。実際に書いて調べてみる。

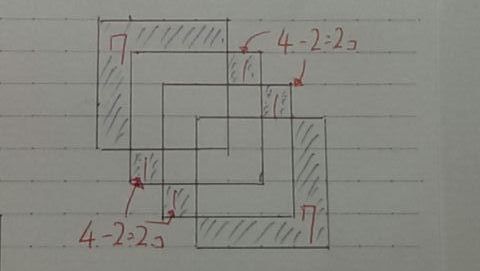
図３で下調べ。４枚重なったときに重ならないのは↑斜線の部分。
ここから右下にどんどん紙を貼り付けていく。
最初と最後の７は変わらない。
１枚貼り付けると上下の端っこの１ｃｍ²がペアで増えていく。
４枚重ねたときに１ｃｍ²の正方形のペアが２組。
つまり、ｎ枚重ねたときは（ｎ－２）個の正方形のペアが増える。
５枚重ねたときも書いてみよう。正方形のペアが３組できる。
よって、７＋７＋（ｎ－２）×２＝１４＋２ｎ－４＝２ｎ＋１０

（３）
小学４年のＳＡＰＩＸ生が類題を解いていたような…中学受験にも出そうな問題。
根気よく調べる。

７枚重ねてみた。２枚重なるところは１８ｃｍ² ↑
最初と最後は５で固定。正方形のペアは上下４組。
つまり、（７－３）個の正方形のペアができる 。
逆にいえば、正方形のペア数＋３＝全体の枚数
試しにやってみると・・
正方形１枚：０ｃｍ²　２枚：０ｃｍ²　３枚：１０ｃｍ²
４枚：１２ｃｍ²　　　５枚：１４ｃｍ² 　・・・
３枚目から１０ｃｍ²で、その後２ｃｍ²ずつ増えていますね。
文字式で書くと、ｎ枚目の紙が２枚重なっている部分の面積の合計は、
５×２＋（ｎ－３）×２＝２ｎ＋４

よって、２ｎ＋４＝３４
２ｎ＝３０　　ｎ＝１５　　　１５枚
公立高校入試解説ページに戻る