2019年度　奈良県公立高校入試問題過去問【数学】解説

平均27.2点（50点満点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）－78.5％

（１）①　97.8％
－５－７＝－12

②　90.1％
２×（－５²）
＝２×（－25）＝－50

③　92.4％
（－３ａ）²×２ｂ÷６ａｂ
＝３ａ

④　85.0％
（ｘ＋２）²－（ｘ＋２）（ｘ－２）
＝（ｘ＋２）{ｘ＋２－（ｘ－２）}　←共通因数（ｘ＋２）でくくる
＝４（ｘ＋２）＝４ｘ＋８

（２）　88.2％
下を上に代入する。
２ｘ－５（ｘ－５）＝－２
ｘ＝９、ｙ＝４

（３）　86.8％
ｘ²－７ｘ－18＝０
（ｘ＋２）（ｘ－９）＝０
ｘ＝－２、９

（４）　62.2％
根号がついているので、すべてを２乗する。
3.3²→10.89
（10/３）²→100/９＝11・１/９
（√11）²→11
よって、10/３が最も大きい。

（５）　72.4％
３×３×π×２＋３×２×π×９
＝72πｃｍ²

（６）　76.5％
円周角の定理から、∠ＢＯＣ（Ａを含まない方）＝116×２＝232°
ｘ＝360－232＝128°

（７）　70.4％
組合せを考える。
全体…₆Ｃ₂＝15通り
ア…₄Ｃ₂＝６通り
イ…₄Ｃ₁×₂Ｃ₁＝８通り
ウ…₂Ｃ₂＝１通り
したがって、最も大きいのはイで、８/15

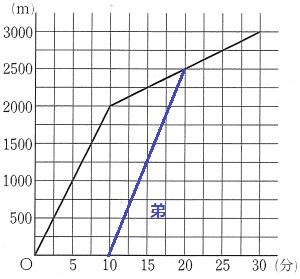
（８）①あ；92.3％、い；76.1％
あ…太郎が自宅から出発して10分後に花子宅へ。そこから20分で図書館に着く。20分後
い…太郎は15分後に2250ｍ歩いているので、3000－2250＝750ｍ

②　61.5％

10分で2500ｍだから、分速250ｍ。

大問２（データの活用）－45.1％

（１）　32.1％！
ア…範囲（レンジ）は最大値－最小値。
Ａ＝27－４＝23　Ｂ＝31－10＝21　Ｂの方が小さい。〇
イ…中央値（メジアン）は真ん中の人の値。
Ａ＝12番目と13番目の平均。（18＋19）÷２＝18.5
Ｂ＝８番目と９番目の平均。18　　Ｂの方が小さい。〇
ウ…最頻値（モード）は最もよく現れた値。
Ａ＝17　Ｂ＝17　ＡとＢで同じ。×
エ…Ａ－３　Ｂ－２。Ｂの方が小さい。○
オ…Ａ：４/24＝0.16…　Ｂ：３/16＝0.187…　Ｂの方が大きい。×
ア・イ・エ
*誤答ではオを含める解答が多かった。

（２）①　70.6％
平均の平均の出し方がおかしい理由。
平均値17.2は25人のデータ。
平均値21.6は15人のデータ。
つまり、17.2は40人中25人、21.6は40人中15人の話で、それぞれ値の重みが違う。
理由の文でいえば、生徒の人数がそれぞれ異なるから。
あ…ウ　い…オ

②ア；42.2％、イ；44.0％
平均の計算・・面倒くさい(´Д｀)
２組…（17.2×25＋21.6×15）÷40＝（430＋324）/40＝18.85→18.9分
３組…（17×18＋21.5×22）÷40＝（306＋473）/40＝19.47→19.5分
ア…18.9分　イ…19.5分

ちなみに、平均の値を直接使って、平均の平均を出すこともできる。
平均値に重み（人数の割合）をかける。
17.2×25/40＝86/８
21.6×15/40＝64.8/８
86/８＋64.8/８＝150.8/８＝18.85→18.9分
重みを掛けて計算する平均を加重平均といいます。

（３）　34.5％
250人中96人が該当者。全体では、
96×2485/250＝47712/50＝954…→950
およそ950人。

大問３（反比例）－39.1％

（１）　89.4％
反比例の比例定数ａ＝ｘｙ＝２×３＝６

（２）　83.5％
積が同じ→ウ

（３）①　9.2％!!
格子点の個数を数える。丁寧に認定していく。

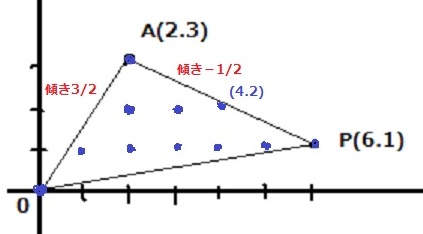
問題のグラフではＰが（１、６）っぽいところにあるが、（６、１）であるのに注意！

横のラインで判定していくのが良いかな？
ＯＡの傾きは３/２。
ｙ＝１のとき、（１、１）は三角形の内部に入るので６個。

ｙ＝２のとき、（１、２）は外部にくる（傾きが２未満だから）。
ＡＰの傾きは－１/２で、（４、２）の点がちょうどＡＰ上にくる→３個。
原点Ｏと点Ａもカウントすること！
１＋６＋３＋１＝11個

②　5.9％!!
まず、Ｃの位置を調べる。
Ｂ（－２、－３）→Ｐ（６、１）
右に８、上に４だから、傾きは１/２
⇒Ｂから〔右２上１〕ずつズラしていくと、ｘ軸との交点Ｃ（４、０）

ＢＤ：ＢＡ＝ａ：ｂとおく。
面積がおのおの等しいので、
ａ×③＝ｂ×④÷２
③ａ＝②ｂ
ａ：ｂ＝２：3
よって、ＢＤ：ＤＡ＝２：１となる。

ＡとＢのｘ座標から、
Ｄのｘ座標は、－２＋４×２/３＝２/３
同様に、Ｄのｙ座標⇒－３＋６×２/３＝１
Ｄ（２/３、１）

大問４（平面図形）－33.9％

（１）　69.9％
作図。
①ＣＤの垂直二等分線。
②Ｄを中心に、ＣＤの中点をＡＤ方向へ移動。

（２）　55.7％
△ＡＢＣ∽△ＥＤＣの証明。

平行四辺形の対角＋辺の１：２
→２辺の比と間の角が等しい→∽

（３）　10.9％！
先ほどの相似を用いる。
ＣＥ：ＣＡ＝ＣＤ：ＣＢ＝１：２
ＣＥ＝①、ＣＡ＝②

△ＡＦＥ∽△ＣＦＢ
ＡＦ：ＦＣ＝９：12＝３：４
ＡＦ＝②×３/７＝○６/７
ＡＦ：ＣＥ＝○６/７：１＝６：７
よって、ＣＥはＡＦの７/６倍。

（４）　3.8％!!
ＢＱ＝○、ＱＣ＝×として、辺を調査していく。

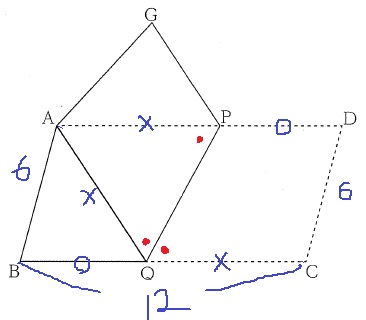
折り返しで、ＱＣ＝ＱＡ
折り返しで、∠ＰＱＣ＝∠ＰＱＡ
錯角から、∠ＰＱＣ＝∠ＱＰＡ
△ＡＱＰは二等辺で、ＡＰ＝×
○＋×＝12だから、ＰＤ＝○

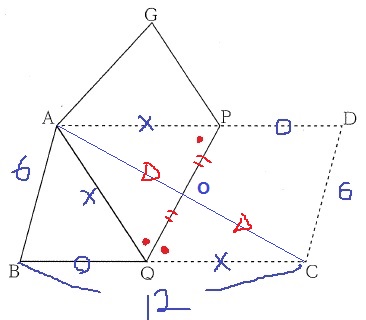
対角線ＡＣを追加。ＡＣとＰＱの交点をＯとおく。
△ＡＯＰ≡△ＣＯＱ（平行線を利用して１辺両端角）
ＡＯ＝ＯＣ、ＰＯ＝ＯＱ
Ｏは平行四辺形の中心点となる。

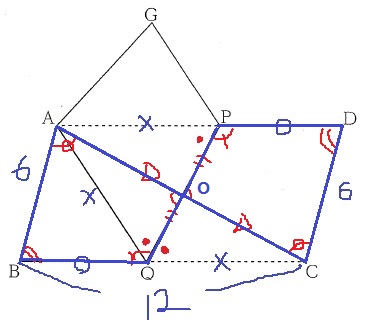
四角形ＡＢＱＯと四角形ＣＤＰＯに着目。
４つの辺が全て等しく、錯角や対頂角、平行四辺形の対角から４つの角も等しい。
四角形ＡＢＱＯ≡四角形ＣＤＰＯ。

求めたい四角形ＡＱＰＧは、折り返しで四角形ＣＱＰＤと同じ。
四角形ＣＱＰＤで、四角形ＯＣＤＰの部分を四角形ＯＱＢＡに移転。
すると、求積すべき図形は二等辺三角形ＡＢＣとなる。

底辺を６ｃｍとすると、高さは、√（12²－３²）＝３√15
６×３√15÷２＝９√15ｃｍ²
求めるべき場所を変えるのがポイント。

＠四角形の合同条件＠
・４辺と１角　・３辺とあいだの２角　・２辺と３角
なぜ、こうなるのか？三角形の合同条件をもとに考えてみよう。
公立高校入試解説ページに戻る