2022年度　福島県公立高校入試問題過去問【数学】解説

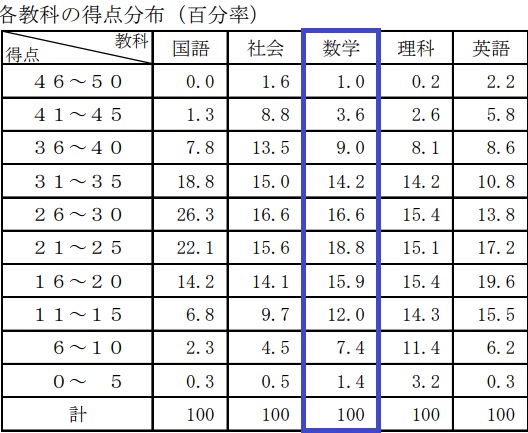
平均24.2点（前年比；±0.0点）

問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）①　99.1％
３－９
＝－６

②　97.3％
７/６×（－12）
＝－14

③　93.4％
５（ａ－２ｂ）－２（２ａ－３ｂ）
＝５ａ－10ｂ－４ａ＋６ｂ
＝ａ－４ｂ

④　88.6％（部分正答0.5％）
√12×√45
＝２√３×３√５
＝６√15

（２）　69.2％（部分正答0.2％）
５×５×π×72/360
＝５πｃｍ²
（*中心角72°は円の５分の１）

大問２（小問集合）

（１）　51.3％（部分正答9.3％）
原稿用紙16枚は16ａｇ。
これに封筒ｂｇを足したら250ｇ以上になった。
16ａ＋ｂ≧250

（２）　86.5％

傾きが正だと右上。切片が負であるウ。

（３）　55.3％（部分正答0.9％）
（ｘ－２）²－６＝０
（ｘ－２）²＝６
ｘ－２＝±√６
ｘ＝２±√６

（４）　80.9％
10人の中央値（メジアン）は５番目と６番目の平均。
11と13の平均で12分。

（５）　68.3％

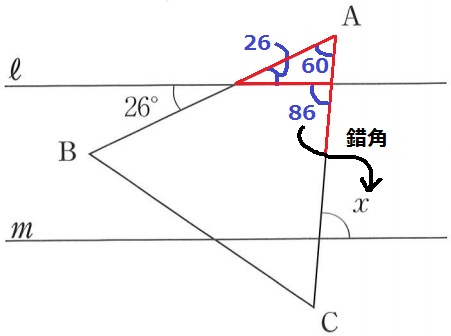
26°を対頂角で右側に移す。
赤線で外角定理を使って、26＋60＝86°
錯角でおろし、ｘ＝86°

大問３（確率＆整数）

（１）①　83.8％
ａ【１、３、５】
ｂ【－２、２】
ｃ【２、４、６】
ａｂ＋ｃ＝－４となる組み合わせを探す。

まず、計算結果が負なので、ｂ＝２だとａ～ｃすべてが正の数になるから不適！
ｂ＝－２が確定。ａｂを計算しておく。
ａｂ【－２、－６、－10】
ｃ【２、４、６】
このうち、条件を満たすのは－６＋２と－10＋６の２通り。

②　56.0％
ｂ＝２のときは必ず正の数になる→０か負の数の方が少ない。
余事象である０か負の数を探す。
ａｂ【－２、－６、－10】
ｃ【２、４、６】
（－２、２）
（－６、２～６）の３通り。
（－10、２～６）の３通り。
計７通り。
全体は３×２×３＝18通り
正の数となる確率は、１－７/18＝11/18

（２）①　67.7％
８段目の左端は８²＝64
８段目には８個の積み木が並ぶ。左端から右端はあいだの数である＋７。
64＋７＝71

②　12.1％！（部分正答27.6％）

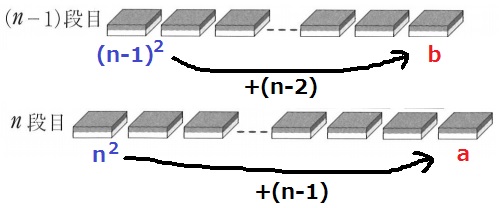
図に文字を書いてしまおう。
再度書くが、左端から右端はあいだの数を足すので〔段数－１〕。
ａ＝ｎ²＋（ｎ－１）＝ｎ²＋ｎ－１
ｂ＝（ｎ－１）²＋（ｎ－２）＝ｎ²－ｎ－１
ａ－ｂ＝（ｎ²＋ｎ－１）－（ｎ²－ｎ－１）＝２ｎ
ｎは自然数なので、２ｎは偶数。
したがって、ａ－ｂは偶数である。ア　

大問４（方程式）

30.8％！（部分正答23.4％）
結果は勝ち・負け・あいこの３通り。
重さで等式を立てるので、それぞれの結果が起きたときにもらえるメダルの重さを算出する。
勝ち…Ａが２枚で10ｇ
負け…Ｂが１枚で４ｇ
あいこ…Ａが１枚、Ｂが１枚で９ｇ

あいこが邪魔なので除外しておく。
あいこを除いた回数は、30－８＝22回
重さは、232－９×８＝160ｇ

そうたが勝った回数をｘ、そうたが負けた回数（ゆうなが勝った回数）をｙとする。
ｘ＋ｙ＝22　…①
10ｘ＋４ｙ＝160　…②
②－①×４をすると、ｘ＝12
ｙ＝22－12＝10
したがって、そうたが勝った回数は12回、ゆうなが勝った回数は10回。

大問５（平面図形）

10.5％!!（部分正答44.9％）
△ＡＢＤ≡△ＡＣＤの証明。

ＡＣ//ＢＥの錯角より、∠ＡＥＢ＝●
△ＡＢＥは二等辺三角形。ＡＢ＝ＡＥなので、ＡＢ＝ＡＣがいえる。
仮定の∠ＢＡＤ＝∠ＣＡＤと共通辺ＡＤをあわせ、２辺とあいだの角が等しいので合同。

＠＠＠

公式解答の２つ目を少々変えて説明すると、四角形ＡＢＥＣは菱形である。
菱形は対角線がおのおのの中点で交わるので、ＢＤ＝ＣＤが導ける。
３辺が等しいから、△ＡＢＤ≡△ＡＣＤとなる。
いずれにせよ、隣り合う辺が等しい点で△ＢＡＥが二等辺であることを指摘する必要がある。

大問６（関数）

（１）　38.5％
Ａはｙ＝ｘ＋４上にある点。
これにｘ＝－２を代入して、ｙ＝－２＋４＝２
Ａ（－２、２）
Ｃはｘ軸についてＡと対称だから、Ｃ（－２、－２）

（２）　26.7％！
同様にｙ＝ｘ＋４にｘ＝４を代入して、Ｂ（４、８）
Ｃ（－２、－２）⇒Ｂ（４、８）
右に６、上に10なので、傾きは10/６＝５/３
Ｃから右に２、上に２×５/３＝10/３あがるから、切片は－２＋10/３＝４/３
ｙ＝５/３ｘ＋４/３

（３）　1.2％!!

△ＰＢＣ：△ＡＣＢ＝①：④
△ＰＢＣが変な形をしているので、これをうまく変形させる。
前問の式、ＢＣ；ｙ＝５/３ｘ＋４/３を利用しよう。

ＡＣがｘ軸に垂直である点に注目。
Ｐを通るＢＣに平行な直線と、半直線ＡＣとの交点をＤとする。
等積変形で△ＰＢＣ＝△ＤＢＣ＝①
△ＡＣＢ：△ＤＢＣ＝④：①で高さ共通だから、底辺の比ＡＣ：ＣＤ＝４：１
ＡＣの距離がちょうど４なので、ＣＤの距離は１である⇒Ｄ（－２、－３）

ＤＰの傾きは５/３。
ｙ＝５/３ｘ＋ｂに（ｘ、ｙ）＝（－２、－３）を代入。
－３＝５/３×（－２）＋ｂ
ｂ＝１/３
ＤＰ；ｙ＝５/３ｘ＋１/３

ＰはＤＰとｙ＝１/２ｘ²の交点。Ｐのｘ座標をｔであらわすと、
１/２ｔ²＝５/３ｔ＋１/３
３ｔ²－10ｔ－２＝０
解の公式を適用。ｔの係数が２で割り切れるのでｂ＝２ｂ’が使える。
ｔ＞０より、ｔ＝（５＋√31）/３

大問７（空間図形）

（１）　61.7％

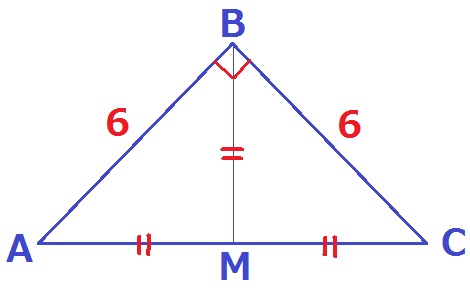
直角二等辺ＡＢＣをＢＭで真っ二つに割ると、△ＡＢＭも直角二等辺。
辺の比は１：１：√２だから、ＢＭ＝６×１/√２＝３√２ｃｍ

（２）①　28.9％！
直角二等辺三角形ＡＢＣの辺の比より、ＡＣ＝６√２ｃｍ

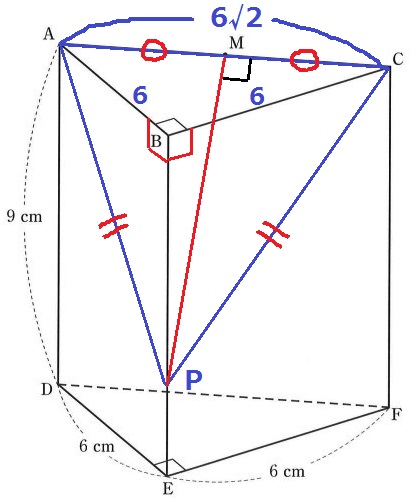
△ＡＰＣの特徴を捉える。
△ＡＢＰと△ＣＢＰに着目すると、ＡＢ＝ＣＢ＝６ｃｍ、
∠ＡＢＰ＝∠ＣＢＰ＝90°、共通辺ＢＰより、２辺と間の角度が等しいので合同。
ＡＰ＝ＣＰより、△ＡＰＣは二等辺三角形である。
（Ｂ・Ｅ・Ｍを通る面で三角柱全体を切断すると左右に二等分される）
ＡＭ＝ＣＭより、ＰＭは頂点Ｐから底辺ＡＣを二等分しているので、
二等辺三角形ＡＰＣの高さにあたる。
30×２÷６√２＝５√２ｃｍ

②　4.6％!!
三角錐Ｂ―ＡＰＣにおいて、底面の△ＡＰＣ＝30ｃｍ²がわかっているから、
あとは三角錐の体積がわかれば、求めたい高さ（距離）がでる。

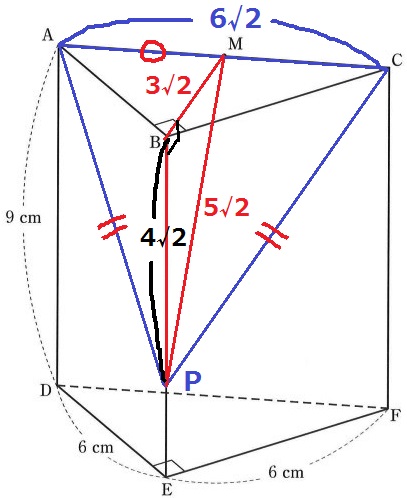
面ＡＢＣとＢＥは直角⇒∠ＭＢＰ＝90°
△ＢＭＰで三平方→辺の比は３：４：５だからＢＰ＝４√２ｃｍ
底面積（△ＡＢＣ）×高さ（ＢＰ）÷底面積（△ＡＰＣ）＝求めたい高さ
６×６÷２×４√２÷30＝12√２/５ｃｍ