平均47.1点(前年比;-14.2点)
問題はこちら→リセマムさん
大問1(小問集合)
(1)
5+(-3)×2
=5-6
=-1
(2)
3xy2÷(-2x2y)×4y
=-6y2/x
(3)
√45+√5-√20
=3√5+√5-2√5
=2√5
(4)
a(a+2)-2(a+2) ←共通因数a+2
=(a-2)(a+2)
=a2-4 ←代入
=(√6)2-4
=6-4=2
(5)
3x+2y=7
2x+y=6
加減法がやりやすいかな?
連立を解いて、x=5、y=-4
(6)
x2+6x-16
=(x+8)(x-2)=0
x=-8、2
(7)
1500円のa割→1500×a/10=150a円
定価-a割
=1500-150a円
(8)
∠PAB=∠PBAをどう使うか。

線対称で対応する角は等しい。
ABの垂直二等分線をひき、ACとの交点がPとなる。
(9)
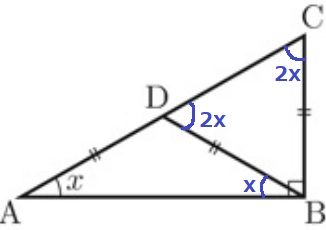
△ABDは二等辺→∠DBA=x
△ABDで外角定理→∠BDC=x+x=2x
△BCDは二等辺→∠BCD=2x
△ABCの内角より、x+2x+90°=180°
x=30°
(10)
最頻値(モード)…最もあらわれている値。
階級値で答えること!
7.0と7.5の平均である7.25秒。
大問2(関数)
(1)
x=0のとき、最小値y=0
x=3のとき、最大値y=9
0≦y≦9
(2)
グラフの式に代入して、座標を確認。
A(1、1)⇒B(3、9)
右に2、上に8だから、傾きは4。
Aから左に1、下に4移動して、切片は1-4=-3
y=4x-3
(3)
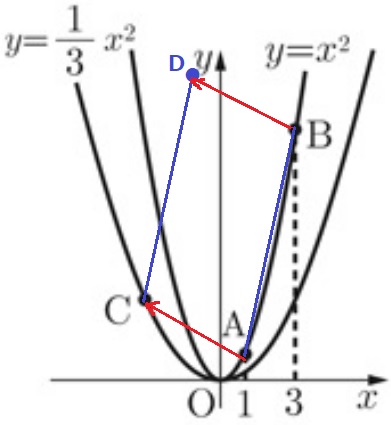
線分ABを平行移動して線分CDに移す。
AがC、BがDに移動する。(Dは必ずしもグラフ上の点ではない)
四角形ABCDは平行四辺形である。
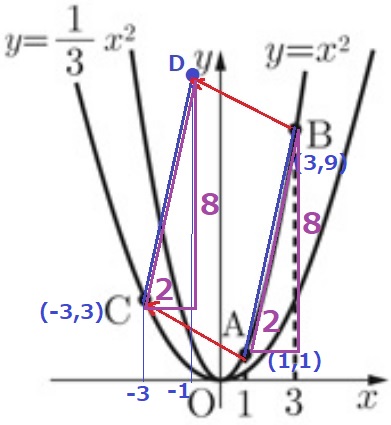
Bから下に8、左に2移動してA。
Dから下に8、左に2移動してC。
Dのx座標が-1だから、Cのx座標は-3となる。
y=1/3x2に代入。
Cのy座標は、1/3×(-3)2=3
Dのy座標は、3+8=11
大問3(確率)
(1)
OB上にくるということは、大・小の目が同じ。
6通りだから、6/36=1/6
(2)
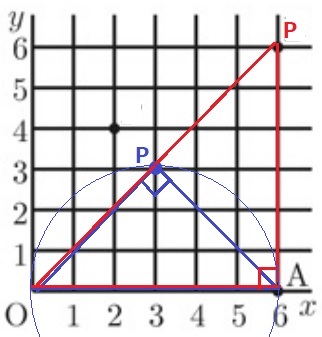
OAの長さは6で固定なので、AO=APからP(6、6)
0は出せないのでこれしかない。
今度はOAを斜辺と捉えると、
OAを直径とする半円の弧に対する円周角からP(3、3)
以上、2通り
2/36=1/18
(3)

Oから半径の長さが4となる円を描く。
気を付けるべき点は、(3、3)は含まない!
Oから(3、3)までの距離は3√2
(3√2)2>42だから、3√2>4となる。
格子点の数は8個。
8/36=2/9
大問4(規則)
(1)

三角形の数に注目。
1番目…1個、2番目…3個、3番目…6個、4番目…10個
6番目の三角形の数は1~6の和。1+2+3+4+5+6=21個
棒の本数は、3×21=63本
(2)

1辺2の正三角形の個数を各段で数えてみると、
2段目1個、3段目2個、4段目3個…10段目9個。
1~9の和を求める。
(1+9)×9÷2=45個
(3)
(1)と同じ考え。
234÷3=78個の正三角形ができるのは何番目か。
数字が小さいので足していった方が早い。
1~10までの和が55だから、
55+11=66
66+12=78!
したがって、12番目
大問5(空間図形)
(1)
△OABは1辺4cmの正三角形。
斜辺を4cmとする1:2:√3の直角三角形より、高さは4×√3/2=2√3cm
4×2√3÷2=4√3cm2
(2)
最短距離なので展開図を作成。
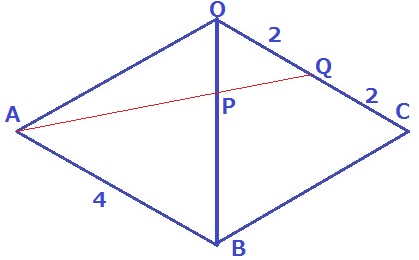
四角形ABCOは1辺4cmの菱形。
△ABP∽△QOPより、OP:PB=OQ:AB=1:2
OB=4cmだから、OP=4×1/3=4/3cm
(3)
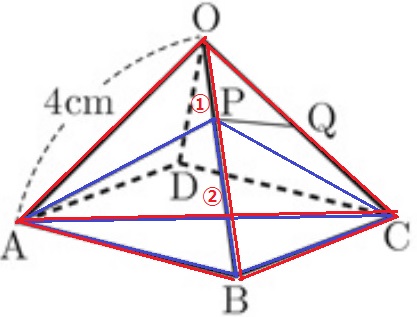
A、C、Pで切断したとき、底面は△ABCになる。
→ポイントは【三角錐O-ABC⇒三角錐P-ABC】
OB:PBがこれらの高さの比にあたる。
PB=4-4/3=8/3cm
OB:PB=4:8/3=③:②
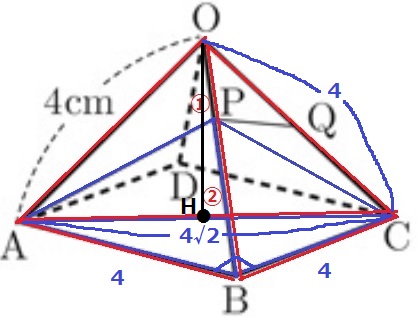
Oの真下をHとする。三角錐O-ABCの高さOHを求める。
△ABCは直角二等辺で辺の比は1:1:√2→AC=4√2
△OACの辺の比を調べると、4:4:4√2=1:1:√2
△OACも直角二等辺である。
それを二等分した△OAHも同様に直角二等辺。OH=4×1/√2=2√2cm
求積すべき体積は、4×4÷2×2√2÷3×2/3=32√2/9cm3
大問6(数量変化)
(1)
6秒後の様子を描く。
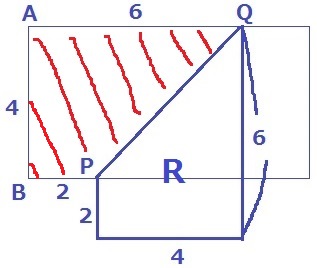
折り返したRは台形ABPQと面積が等しい。
y=(6+2)×4÷2=16
(2)
転換点に注意する。

Rは折り返された部分と合同。
0≦x≦4では、△APQの底辺と高さがともに伸びる。
面積はy=ax2で増加し、x=4のとき、y=4×4÷2=8
4≦x≦8では、台形ABPQは上底と下底が伸びる。
面積は一次関数で増加し、x=8のとき、y=(8+4)×4÷2=24
8≦x≦10では、△DPQの部分が底辺のみ伸びる。
面積は一次関数で増加し、x=10のとき、y=24+2×4÷2=28
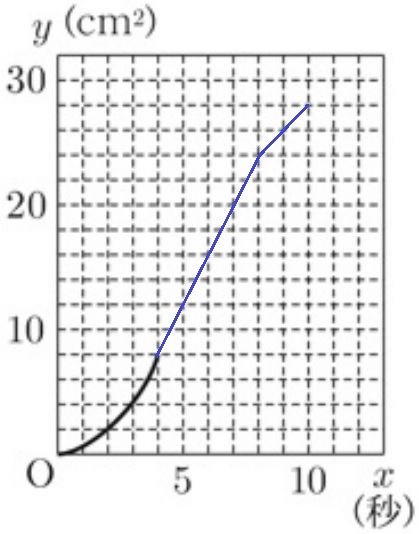
↑まとめるとこうなる。
(3)
ここも転換点に気を付けながら調べる。

0≦x≦4はSとRは同じ。
4≦x≦8はSは等積のまま右に移動する。
8≦x≦10は高さが小さくなるので、Sの値も小さくなる。
オ
(4)
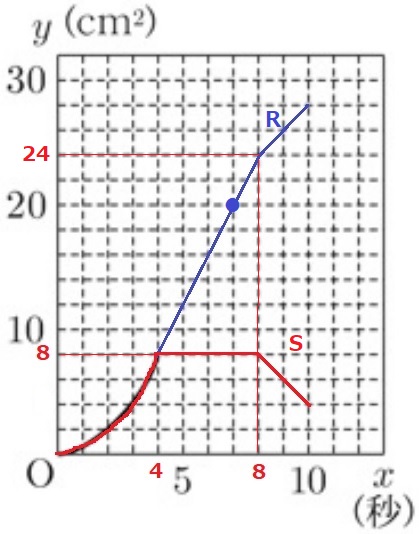
先ほどのグラフにRを描く。
Sの面積が8cm2のときが長いので、このときのRを計算すると、
R=8×5/2=20cm2
グラフより7秒後
大問7(平面図形)
(1)
△ABD∽△O’BPの証明。
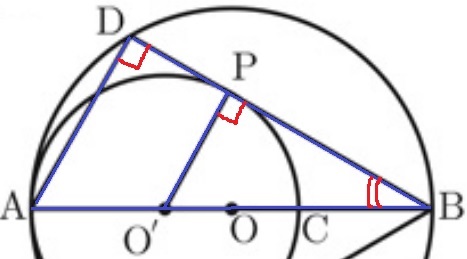
1つは共通角。
半径OPと接線DBは垂直だから、∠O’PB=90°
半円の弧に対する円周角である∠ADB=90°
2角が等しいので∽
(2)①
ここから難しくなります。
PEが変な位置にあるので、図形の特徴をつかむために少し調べる。
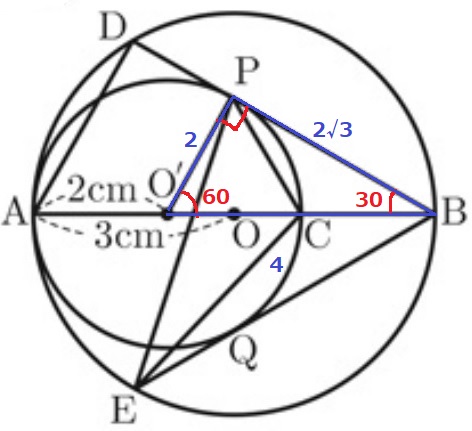
O’P=2cm、O’B=4cm、∠O’PB=90°から、
△O’BPの辺の比が1:2:√3である直角三角形であることに勘づきたい。
∠PBO’=30°
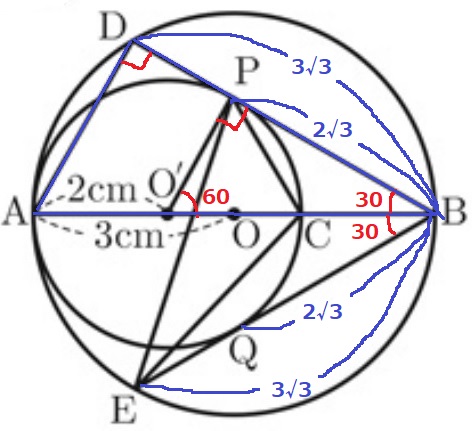
前問で△ABD∽△O’BPだから、△ABDの辺の比も1:2:√3
AB=6cmより、BD=6×√3/2=3√3cm
BDとBEは円O’の接線であり、PとQはそれぞれの接点である。
円外の点から接点までの距離(接線の長さ)は等しいので、BQ=BP=2√3cm
その延長線でBから円Oとの交点までの距離も等しく、BE=BD=3√3cm
ようするに、直径ABを対称の軸としてこれらが上下で線対称の関係にある。
∠O’BQ=30°
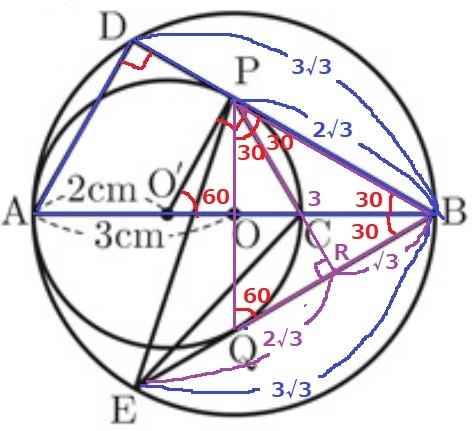
ごちゃごちゃして申し訳ない(;`ω´)
PからBEに向けて垂線、その足をRとする。
△BPRの内角も30°-60°-90°で1:2:√3から、PR=3cm、BR=√3cm
(△O’CPは正三角形で∠BPC=30°。すなわち、CはPR上にある)
ER=3√3-√3=2√3cm
△PREで三平方→PE=√21cm
*ちなみに、△BPQは正三角形。
②
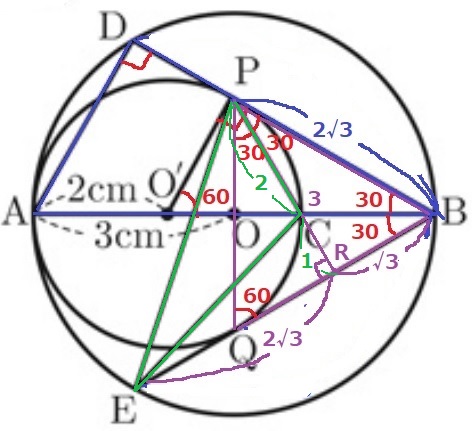
△BCRも1:2:√3→CR=1cm
PC=3-1=2cm
△CPEは底辺PCで高さERだから、2×2√3÷2=2√3cm2
●講評●
大問1
ここはミスを最小限におさえたい。
大問ごとの後ろの小問がやりにくいので重要な得点源。
大問2
(3)Dは必ずしもグラフ上の点とは限らない。
ここを踏まえないとおかしくなる。
大問3
(2)いろいろありそうだが2通りしかない。
OAが斜辺かそうでないかで場合分けが良いかも。
(3)(3、3)は含まない!
大問4
(2)ここも問題文の条件を的確に。段ごとで調べると規則がある。
大問5
(3)断面APCを作図⇒底面は四角形ABCDではなく△ABC。
前問から高さの比。正四角錘の高さも素早く求めたい。
大問6
(2)(3)時間が足りないので、要領良く調べ上げたい。
大問7
(2)①PEを1辺とする直角三角形が見当たらないので作る。
辺の比に注意して1:2:√3を早々に気がつきたい。
問題文に角度の情報がないので見つけにくいが、図形問題でつまったら角度の調査!
円の中心OとO’が直径AB上にあり、2本の接線から上下で線対称。
処理自体は多くはないが、図形の特徴を正確にひもとくのが大変な問題であった。
30°か60°がでたら垂線をひくと便利な直角三角形がつくれる。ぜひ応用してみよう。



コメント