平均点23.3点（前年比；＋0.4点）
問題はコチラ→ＰＤＦファイル
大問１（計算）
（１）
0.5×0.7
＝0.35
（２）
－９＋８÷４
＝－９＋２
＝－７
（３）
（ｘ＋３ｙ）/４＋（７ｘ－５ｙ）/８
＝｛２（ｘ＋３ｙ）＋（７ｘ－５ｙ）｝/８
＝（２ｘ＋６ｙ＋７ｘ－５ｙ）/８
＝（９ｘ＋ｙ）/８
（４）
６ａｂ÷（－９ａ2ｂ2）×３ａ2ｂ
＝－２ａ
（５）
（２ｘ－３）2－４ｘ（ｘ－１）
＝４ｘ2－12ｘ＋９－４ｘ2＋４ｘ
＝－８ｘ＋９
（６）
（√６－２）（√３＋√２）＋６/√２
＝３√２＋２√３－２√３－２√２＋３√２
＝４√２
大問２（小問集合）
（１）
３ｘ－７＝８－２ｘ
５ｘ＝15
ｘ＝３
（２）
２ｘ2＋７ｘ＋１＝０
解の公式を適用して、ｘ＝（－７±√41）/４
（３）①
14人の中央値（メジアン）は７番目と８番目の平均。
12と14の平均→13ｍ
②
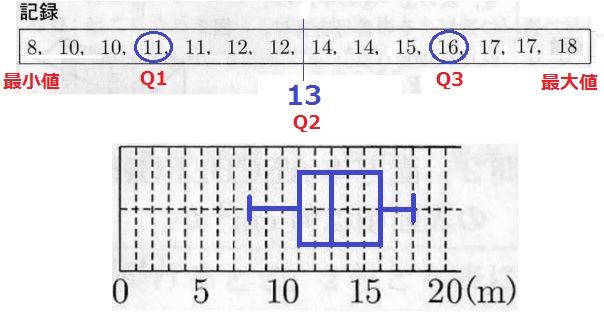
第２四分位数（Ｑ2；中央値）が13ｍ。
第１四分位数（Ｑ1）は、下位７人の中央値11ｍ（下から４番目）。
第３四分位数（Ｑ3）は、上位７人の中央値16ｍ（上から４番目）。
最小値８ｍ、最大値18ｍ。 以上をもとに描くと、うえの箱ひげ図になる。
（４）
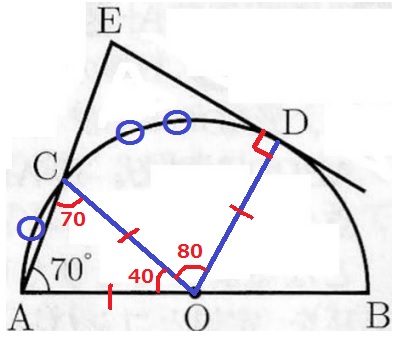
半径から△ＡＯＣは二等辺三角形。
∠ＣＯＡ＝180－70×２＝40°
中心角の大きさは弧の長さに比例する。 ∠ＣＯＤ＝40×２＝80°
半径は接線と直交する→∠ＯＤＥ＝90°
四角形ＡＯＤＥの内角より、∠ＣＥＤ＝360－（70＋120＋90）＝80°
（５）
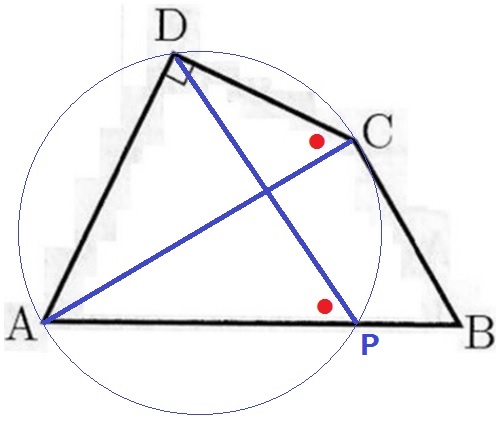
試しに、∠ＡＰＤ＝∠ＡＣＤとなるようなＰをＡＢ上に描いてみる。
ＣとＰがＡＤについて同じ側にあって２つの角が等しいから、
円周角定理の逆より４点Ａ、Ｐ、Ｃ、Ｄは同一円周上にある。
→この円の中心の位置が知りたい。
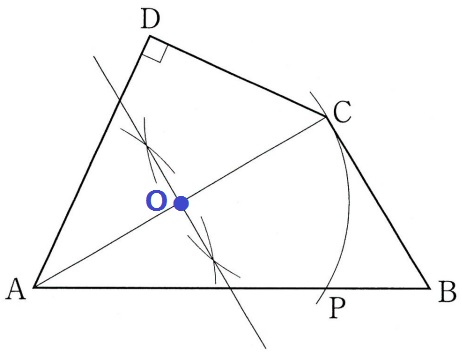
円の中心ＯはＡＤとＤＣそれぞれの垂直二等分線の交点である。
それでも良いが、では公式解答は何をやってるかというと、
直径に対する円周角は90°なので、∠ＡＤＣ＝90°から直径はＡＣ。
この中点が中心Ｏである。
①ＡＣの垂直二等分線、円の中心Ｏを特定。
②半径ＯＣの長さをＡＢ上に移す。円周とＡＢの交点がＰ。
（６）①
小問扱いだが、問題文が長くなる(´ﾟωﾟ)
条件を整理する。
●３個同色→和
●２個同色→同×同＋異
１×２＋３＝５点
②
全体は、2Ｃ1×4Ｃ2＝12通り
得点が奇数になる組み合わせを調べる。
●赤３個
（１＋０＋２）の１通り。
●赤２個＋白１個
白がＡの偶数２の場合、Ｂの赤２個の積は奇数である。
しかし、そのような組み合わせはない。
白がＢの奇数３の場合、赤２個の積は偶数である。
（１×０＋３）（１×２＋３）の２通り。
●赤１個＋白２個
白の積は２×３＝６と偶数なので、Ｂの赤は奇数である。
（２×３＋３）の１通り。
合計４通りで、確率は４/12＝１/３
（７）①
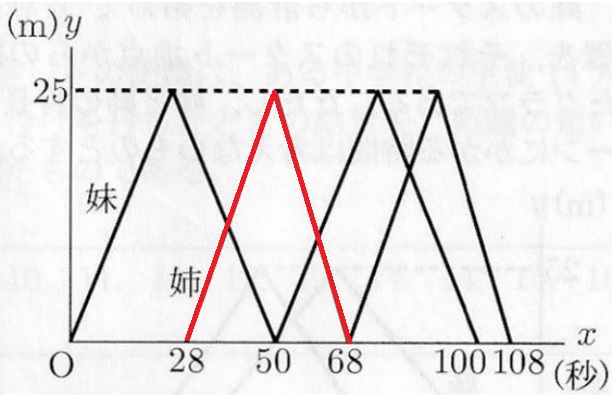
２回目にすれちがった場所は●の交点。
妹は片道25秒ずつなので、1.5往復は75秒後。
姉の片道は28と68の平均で48秒後。
青線の相似に着目する。 相似比は、27：18＝３：２
姉の48～68秒の20秒間の時間を⑤とすると、③＝20×③/⑤＝12秒
交点の時間は、48＋12＝60秒後
②
情報を整理する。
妹は前日と同じ速さで２往復するので様子は変わらない。
姉のゴールも８秒遅れで変わらず、２往復目のクロールの速さも変わらない。
ということは、姉の１往復目（平泳ぎ）だけが変わっている。
姉の１往復目のゴールは68秒後。
グラフの赤線部分だけを変えて、２回目のすれ違いが58秒後になるようにする。
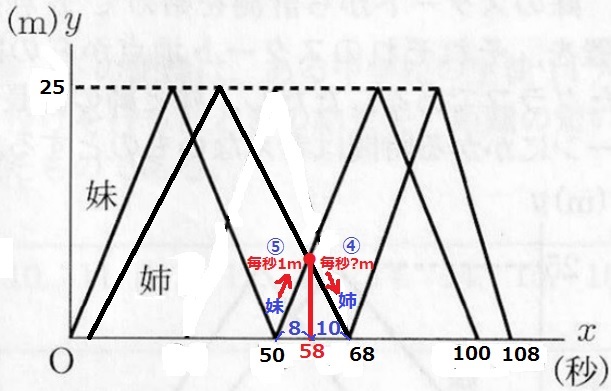
赤線に着目する。 この距離を妹は８秒、姉は10秒の時間で泳いだ。
速さの比は時間の逆比、妹：姉＝10：８＝⑤：④
妹の速さは25ｍ÷25秒＝毎秒１ｍだから、姉の速さは１×④/⑤＝毎秒0.8ｍ
姉の１往復の時間は、50÷0.8＝62.5秒
姉のスタートは、68－62.5＝5.5秒後
ａ＝5.5、ｂ＝0.8
大問３（データの活用）
（１）①
ア：最頻値（モード）は最もあらわれている値。
値といっても、度数ではなく階級値の37.5ｋｇ。×
イ：累積度数とは、最も小さい階級からその階級までの度数の合計。
45ｋｇ以上の度数が２＋１＝３人なので、45ｋｇ未満の和は15－３＝12人。〇
ウ：範囲（レンジ）＝最大値－最小値
表１は25-30ｋｇと50-55ｋｇがなく、表２より範囲は小さい。×
エ：４/25＜３/15＝１/５＝５/25。〇
イ・エ
②
答案では累積相対度数を用いて理由を説明する。
各々の確率を出して比較すれば良い。
●１組の計25人から１人を選ぶ。 （０＋４＋11）/25＝0.6
●１組と２組の計40人から１人を選ぶ。 （15＋１＋３＋３）/40＝0.55
0.6＞0.55だから、アの方が40ｋｇ未満が選ばれやすい。
（２）
下の長方形は、美咲の現実の握力（21ｋｇ）のときの15人の総和。
もし、美咲の握力がａｋｇでもう少し強かったら、
赤い長方形が追加されて15人の平均値は＋0.4ｋｇ増える。
15人の総和の増加分（赤い長方形）面積は、0.4×15＝６ｋｇ
現実の美咲の握力は21ｋｇだから、ａ＝21＋６＝27
後半は赤い長方形の面積を40人で均せばいい。
40人の平均値の増加分は、ｂ＝６÷40＝0.15
ア…27、イ…0.15
大問４（空間図形）
（１）
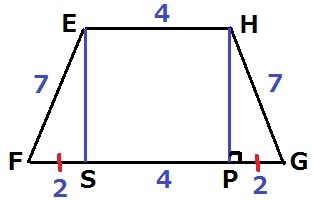
Ｅから垂線をおろし、足をＳとする。
ＳＰ＝ＥＨ＝４ｃｍ
四角形ＥＦＧＨは等脚台形で左右対称だからＳＦ＝ＰＧ。
ＰＧ＝（８－４）÷２＝２ｃｍ
（２）
△ＨＰＱで三平方→ＨＰ＝３√５ｃｍ
（３）
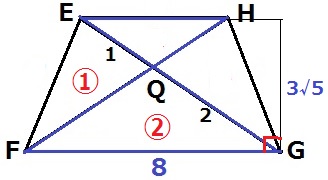
△ＥＱＨ∽△ＧＱＦで、ＥＱ：ＱＧ＝１：２。
△ＥＦＱ：△ＱＦＧ＝①：②
【△ＥＦＧ⇒△ＥＦＱ】
８×３√５÷２×①/③＝ ＝４√５ｃｍ2
（４）
三角錐Ｒ―ＥＦＱにおいて底面積は△ＥＦＱ＝４√５ｃｍ2
高さがわかれば、三角錐の体積が求まる。
ＲはＣＥと△ＡＦＨの交点。
Ｒの位置を特定するために、ＣＥを含む面ＡＥＧＣに着目する。
前問の相似から、ＥＱ：ＱＧ＝１：２→ＡＣ＝３
△ＡＲＣ∽△ＱＲＥより、ＥＲ：ＲＣ＝①：③
三角錐の高さは、10×①/④＝５/２ｃｍ
三角錐Ｒ―ＥＦＱの体積は、４√５×５/２÷３＝10√５/３ｃｍ3
大問５（関数）
（１）
ｙ＝ａｘ2にＡの座標（４、４）を代入する。
４＝16ａ
ａ＝１/４
（２）
ｙ＝－ｘ2にｘ＝－２を代入して、Ｂ（－２、－４）
Ｃはｙ軸に関してＢに対称だから、Ｃ（２、－４）
Ｃ（２、－４）⇒Ａ（４、４）
右に２、上に８移動して傾きは４。
Ｃから左に２、下に８移動して、切片は－４－８＝－12
ｙ＝４ｘ－12
（３）①
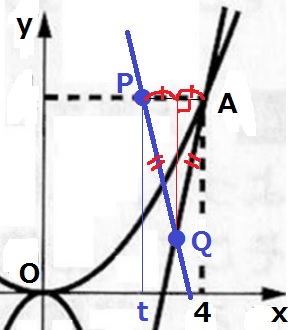
ＱＡ＝ＱＰだから、△ＡＰＱは二等辺三角形。
底辺ＰＡの垂直二等分線上にＱがあるので、Ｑのｘ座標はＰとＡの平均。
（ｔ＋４）÷２＝１/２ｔ＋２
②
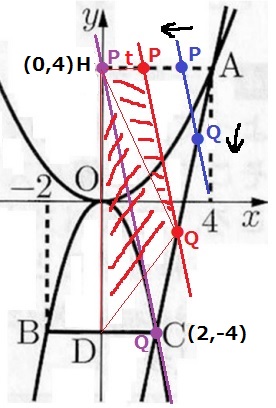
まずは動きを確認します。
ＰはＡＨ上、ＱがＡＣ上の点で、ＡからＰを左、Ｑを左下に移動させてみる。
△ＡＰＱは常に二等辺三角形で、ＰがＨに着くとＱはちょうどＣに着く。
△ＱＨＤは底辺ＨＤ＝８で固定、高さが減少するので面積は減少する。
△ＰＨＱは底辺ＰＨ＝４、高さ０の状態から面積が増加、
終わりは底辺ＰＨ＝０、高さ８で面積が０に戻る。
…ということは、△ＰＨＱの面積は途中まで増加してどこかで減少に転ずる。
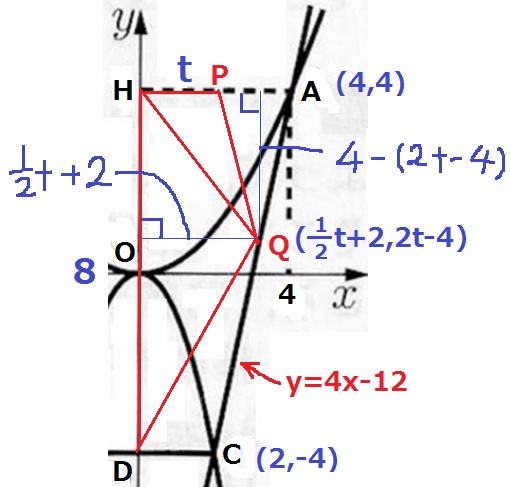
Ｐのｘ座標がｔ、Ｑのｘ座標は前問より１/２ｔ＋２。
Ｑのｙ座標は、ｙ＝４ｘ－12にｘ＝１/２ｔ＋２を代入して、
ｙ＝４×（１/２ｔ＋２）－12＝２ｔ－４
△ＱＨＤ…８×（１/２ｔ＋２）÷２＝２ｔ＋８
△ＰＨＱ…ｔ×｛４－（２ｔ－４）｝÷２
＝－ｔ2＋４ｔ
３（－ｔ2＋４ｔ）＝２ｔ＋８
３ｔ2－10ｔ＋８
＝（３ｔ－４）（ｔ－２）＝０
ｔ＝４/３、２
ＰはＡＨ上の点だから、０≦ｔ≦４で条件に適する。
＠余談＠
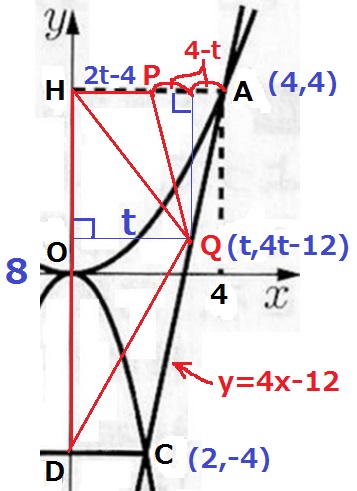
Ｑのｘ座標をｔにおいた方がいんじゃね？(･Д･)
と思って試したら、△ＰＨＱがひどかったです(;`ω´)
△ＱＨＤ…８×ｔ÷２＝４ｔ
△ＰＨＱ…（２ｔ－４）（－４ｔ＋16）÷２
＝２（ｔ－２）（－４ｔ＋16）÷２＝－４ｔ2＋24ｔ－32
３（－４ｔ2＋24ｔ－32）＝４ｔ
12ｔ2－68ｔ＋96＝０
３ｔ2－17ｔ＋24＝（３ｔ－８）（ｔ－３）＝０
ｔ＝８/３、３
２ｔ－４＝４/３、２
素直に誘導に従いましょう(;`ω´)
大問６（平面図形）
（１）
△ＡＢＥ∽△ＢＣＧの証明。
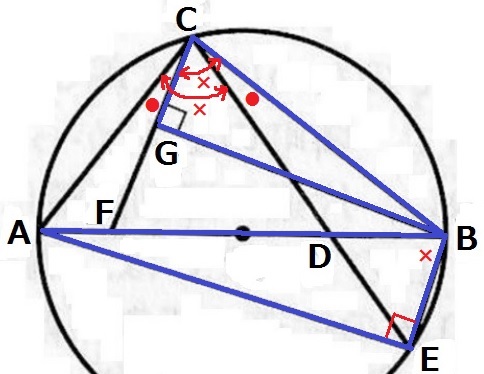
直径に対する円周角で∠ＡＥＢ＝90°
∠ＡＢＥ＝×として、弧ＡＥの円周角より∠ＡＣＥ＝×
仮定より∠ＡＣＦ＝∠ＢＣＤ＝●とおく。
∠ＡＣＥ（×）＝●＋∠ＦＣＤ＝∠ＢＣＧ（×）
90°と×の２角が等しく∽。
（２）
ＣＧは△ＢＣＧの１辺。
前問の△ＡＢＥ∽△ＢＣＧを使うのだろうと想像する。
ＣＧに対応するＢＥの長さが知りたいところ。
△ＡＢＣに着目すると、ＡＣ：ＡＢ＝６：10＝３：５
辺の比が３：４：５の直角三角形だから、ＢＣ＝８ｃｍ
ここから悩む(´～`)
△ＣＡＤが二等辺三角形であることに着目する。
Ｃから垂線をひき、ＡＤとの交点をＨとする。
直角三角形の頻出の相似形、２角相等で△ＡＢＣ∽△ＡＣＨ。
ＡＣ＝⑤とおくと、ＡＨ＝③
また、ＣＨは二等辺三角形ＣＡＤを２等分するので、ＤＨ＝ＡＨ＝③
ＡＤ＝６×⑥/⑤＝36/５ｃｍ
ＤＢ＝10－36/５＝14/５ｃｍ
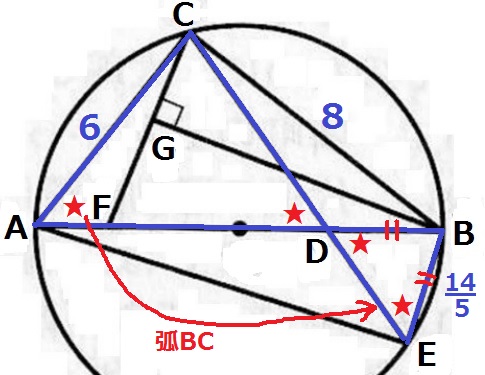
二等辺三角形ＣＡＤの底角を★とする。
対頂角で∠ＢＤＥ＝★、弧ＢＣの円周角で∠ＢＥＤ＝★
△ＢＤＥも二等辺だから、ＢＥ＝ＢＤ＝14/５ｃｍ
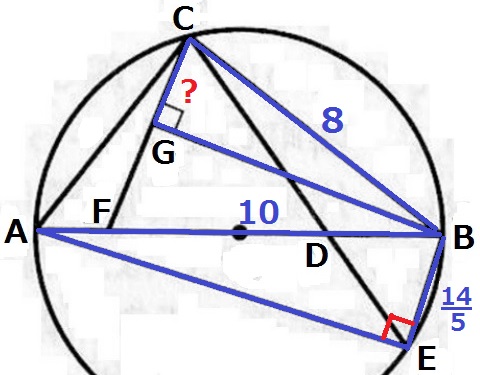
最後に△ＡＢＥ∽△ＢＣＧ。
ＣＧ＝14/５×８/10＝56/25ｃｍ
大問１
ここだけで配点が10点もある。
大問２
（４）円周上の点と円の中心を結ぶと何とかなる。
（５）円周角で２つの角が等しくなる。円を描くには中心が必要。
（６）条件がやや複雑。ここでまごつくと時間配分が危うくなる。
②赤は３～１個（白は０～２個）の３通り。
それぞれのなかで条件に合う組み合わせを調べ上げる。
（７）大問が６個もあるのに、ここの２問で時間を消費してしまう。。
①グラフ上で相似を使うと処理が速い。
②姉の平泳ぎだけが変わる。
58秒後の出会いから、姉の平泳ぎの速さが先に求まる。
大問３
（１）②おのおのの累積相対度数を比べればＯＫ。
（２）解説では中学受験の面積図で解いた。
大問４
次の小問の前提になるのでドミノ倒しの危険がある。
（１）等脚台形は公立入試でよく登場する。
（３）同様。高得点を狙うには、ここまで時間をかけたくない。
（４）ＣＥを含む面で切り取る。ＲはＣＥとＡＱの交点。
大問５
（３）①二等辺三角形の底辺ＰＡの垂直二等分線上にＱがある。
②処理が大変(´ﾟдﾟ｀)50分で間に合うのか？Ｑのｙ座標がポイント。
大問６
（１）ある角の左右に等角がある。∠ＡＣＥを∠ＢＣＧにズラす。
（２）ここも大変。対応する辺に狙いをしぼる。
ＡＢ＝10ｃｍに対応するＢＣは直角三角形ＡＢＣからわかる。
△ＡＢＥと△ＢＣＧの相似比がでるので、ＣＧに対応するＢＥが知りたい。
３：４：５の辺の比を二等辺三角形で使う。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント