2021年度　長崎県公立高校入試・後期過去問【数学】解説

問題はコチラ→ＰＤＦファイル
出題範囲の縮小は中２の確率、中３の円と標本調査。

大問１（小問集合）

（１）
（３²－１）÷（－２）
＝８÷（－２）
＝－４

（２）
√45－10/√５
＝３√５－２√５
＝√５

（３）
反比例の比例定数ａは積ｘｙで一定。
ｙ＝４×８÷２＝16

（４）
配る予定の個数は４ｘ個。
しかし、30個ではｙ個不足する。
４ｘ＝30＋ｙ
４ｘ－ｙ＝30

（５）
ｘ＋２ｙ＝－１　…①
３ｘ－４ｙ＝17　…②
①×２＋②をすると、５ｘ＝15
ｘ＝３
①に代入して、ｙ＝－２
ｘ＝３、ｙ＝－２

（６）
（ｘ－２）²－５＝０
（ｘ－２）²＝５
ｘ－２＝±√５
ｘ＝２±√５

（７）

同位角で74°を上げる。
外角定理を適用して、ｘ＝110－74＝36°

（８）
最も大きい数⇒5000
千の位が４⇒4100、4010、4001
千の位が３⇒3200
５番目は3200。

（９）

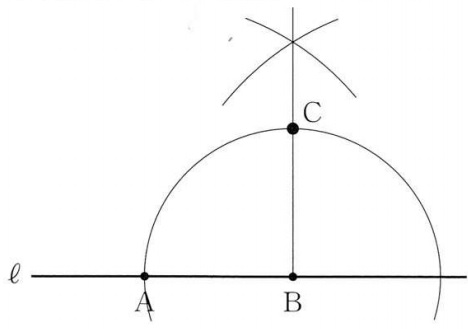
①∠ＡＢＣ＝90°だから、Ｂを通る垂線を引く。
②ＡＢの長さを垂線へ移す。

（10）

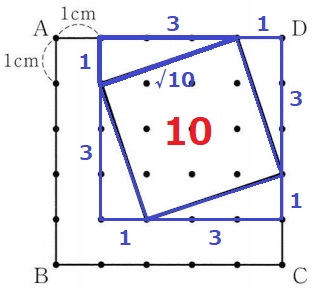
10は平方数ではないので、正方形の１辺は斜めになると予測する。
直角三角形の２辺をａ、ｂとすると、
三平方の定理より、ａ²＋ｂ²＝３²＋１²＝10
斜辺以外の長さが３ｃｍ、１ｃｍである直角三角形の斜辺√10ｃｍが正方形の１辺となる。

大問２（データの活用・整数）

（１）①
７÷20＝７/20=35/100=0.35

②
（０×０＋１×１＋２×４＋３×７＋４×２＋５×６）÷20
＝68÷20＝3.4冊

③
①：１年２冊の相対度数は４÷20＝0.20で１年生の方が大きい。〇
②：２年４冊以上は25×0.36＝９人で２年生の方が大きい。×
③：２年生の最頻値は相対度数が最も大きい３冊で１年生と同じ。×
④：１年生の中央値は10番目と11番目の平均⇒３冊
２年生の中央値は相対度数の和が0.5以上に達する３冊で同じ。〇
①、④

（２）①ア
中央が８のとき、周りの４つの和が32だった。
周り４つの和＝中央×４
中央の数は、44÷４＝11

②

８を中心に数字の位置関係が対称的がある。
こういう場合は中央の数ｃをｘとおく。
残りの４つの数はｘ－７、ｘ－１、ｘ＋１、ｘ＋７。
イ…ｃ、ウ…ｘ＋７

③
Ｐ＝ａ＋ｂ＋ｃ＋ｄ
＝（ｘ－７）＋（ｘ－１）＋（ｘ＋１）＋（ｘ＋７）
＝４ｘ
ｘは整数だから、４ｘは４の倍数。
したがって、中央以外の４つの数の和は４の倍数になる。

大問３（関数）

（１）
ｙ＝ｘ²にｘ＝２を代入。
ｙ＝２²＝４

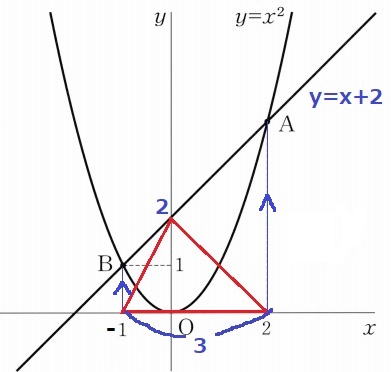
（２）
ｙ＝ｘ²にｙ＝１を代入してＢ（－１、１）
Ｂ（－１、１）⇒Ａ（２、４）
右に３、上に３だから傾きは１。
Ｂから右に１、上に１移動して切片は２。
ｙ＝ｘ＋２

（３）
ｘ＝０のとき、最小値ｙ＝０
ｘ＝－２のとき、最大値ｙ＝４
０≦ｙ≦４

（４）

△ＯＡＢは幅３、高さ２だから、３×２÷２＝３

（５）

ｙ＝ｘ＋２にｙ＝０を代入してＤ（－２、０）
Ｃ（０、２）を通る傾き－１の直線はｙ＝ｘ＋２とｙ軸上の（０、２）で交わる。
この点をＥとする。
２つの直線の傾きの積が－１だから垂直に交わる！

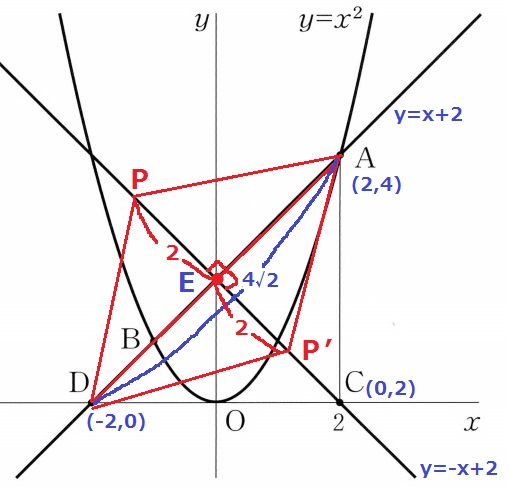
△ＡＣＤは直角二等辺三角形。
１：１：√２より、ＡＤ＝４√２

△ＡＰＤの高さは、４√２×２÷４√２＝２
つまり、ＰＥ＝２となればいい。
傾き－１⇒１：１：√２より、Ｐのｘ座標は－√２と√２。

大問４（空間図形）

（１）
側面積は展開図にすると長方形になる。
縦は円柱の高さ４ｃｍ、横は底面の円周。
４×６π＝24πｃｍ²

（２）
２×２×π×４÷３＝16/３πｃｍ³

（３）

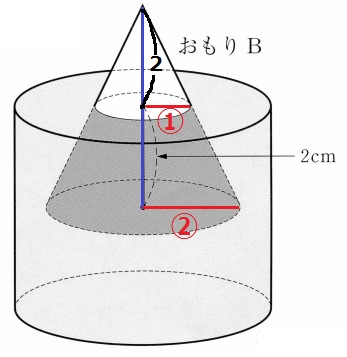
おもりが沈んだ分だけ水があふれる。
体積比は相似比の３乗→水面上：おもり全体＝１³：２³＝１：８
水面上：水面下＝１：７
16/３π×７/８＝14/３πｃｍ³

（４）

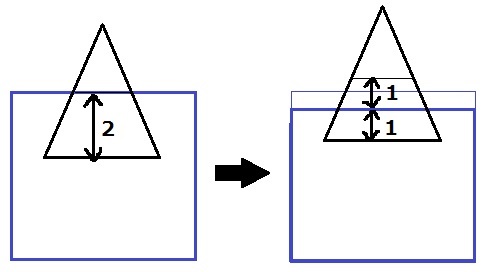
おもりを上げると、おもりの底面から水面までの高さが２ｃｍから１ｃｍになった。
こういうタイプの問題は、変化の前後で体積が同じ場所を見つける。

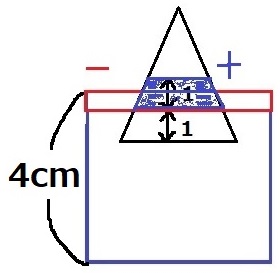
赤枠は水面が下がったところ。
赤枠のマイナス分は、変化前は水面下にあったが変化後に水面より上にくる青いプラスの部分と体積が等しい。
（両者は重複部分もあるが、それを含めて体積が等しい）
青い部分の体積⇒赤枠の体積を円柱の底面積で割る⇒４ｃｍから下がった水面の高さを引く。

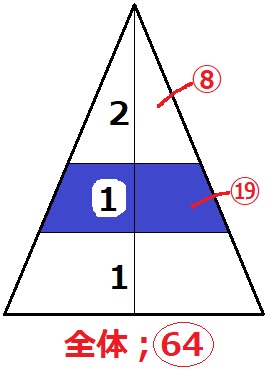
おもり全体の体積比は、４³＝〇64
青い部分の体積比は、３³－２³＝⑲
青の体積は、16/３π×⑲/〇64＝19/12πｃｍ³

下がった水面の高さは、19/12π÷９π＝19/108ｃｍ
水面の高さは、４－19/108＝413/108ｃｍ

大問５（平面図形）

（１）
菱形の定義は『４辺が等しい四角形』
平行四辺形は対辺が等しい。
これにくわえて隣り合う辺が等しくなれば、４辺が等しくなって菱形。
④
*菱形の性質は『２本の対角線が垂直に交わる』
ＰＲ⊥ＳＱでも菱形になる。菱形は特別な平行四辺形。

（２）
△ＡＰＳ≡△ＣＲＱの証明。

仮定よりＡＰ＝ＣＲ
平行四辺形の対辺でＰＳ＝ＲＱ
長方形の内角から∠ＰＡＳ＝∠ＲＣＱ
斜辺と他の１辺が等しい直角三角形より合同。

（３）

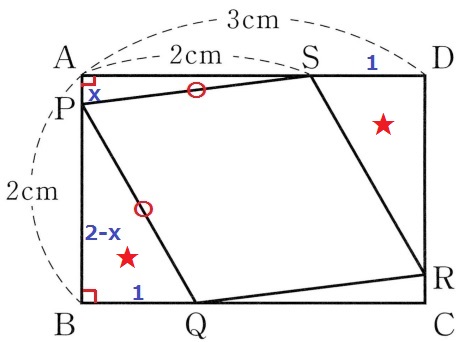
求めたいＡＰをｘとおく。
ＰＢ＝２－ｘ
前問の△ＡＰＳ≡△ＣＲＱと同じ要領で△ＢＰＱ≡△ＤＲＳ
対応する辺からＢＱ＝ＤＳ＝１ｃｍ

四角形ＰＱＲＳは菱形だから、ＰＳ＝ＰＱ
△ＡＰＳと△ＢＰＱの斜辺が等しい⇒三平方の定理で等式。
ＡＰ²＋ＡＳ²＝ＢＰ²＋ＢＱ²
ｘ²＋２²＝（２－ｘ）²＋１²
ｘ²＋４＝４－４ｘ＋ｘ²＋１
４ｘ＝１
ｘ＝１/４
ＡＰの長さは１/４ｃｍ

（４）①
錯角で∠ＡＳＢ＝60°
△ＡＢＳの内角は30°―60°―90°だから、辺の比が１：２：√３の直角三角形。
菱形よりＢＳ＝ＢＱ＝８√３ｃｍ
ＡＢの長さは、８√３×√３/２＝12ｃｍ

②

ひとまず長方形全体を調べてみる。
ＱＣ＝ＡＳ＝12×１/√３＝４√３ｃｍ
菱形ＥＦＧＨの面積…対角線×対角線÷２＝12√３×12÷２＝72√３ｃｍ²
左右の不要な２つの三角形を除けば斜線部分が出る。

直角三角形ＢＥＦに着目する。
ＥＢ＝12÷２＝６ｃｍ
ＢＦ＝12√３÷２＝６√３ｃｍ
ＥＢ：ＢＦ＝６：６√３＝１：√３
辺の比が１：２：√３の直角三角形で、内角は30°―60°―90°である。

角度の調査。ＢＳとＥＦ、ＥＨの交点をそれぞれＩ、Ｊとする。
∠ＢＥＦ＝60°、∠ＡＢＳ＝30°
→∠ＥＩＢ＝90°となり、ＢＳとＥＦは直交する。

△ＡＥＨ≡△ＢＥＦより∠ＡＥＨ＝60°
∠ＪＥＩ＝180－60×２＝60°
→△ＥＩＪの内角も30°ー60°ー90°で辺の比は１：２：√３
ＥＩ＝６×１/２＝３ｃｍ
ＩＪ＝３√３ｃｍ

図形全体が点対称。対称性から右側の三角形も△ＥＩＪと合同である。
求積すべき図形の面積は、72√３－３×３√３÷２×２＝63√３ｃｍ²

大問６（文章題）

（１）
◆令子が１を選ぶ
和男は２・３を同時に取れないので令子が勝つ。
◆令子が２を選ぶ
和男が３を選べば１・３を取れる。令子の負け。
◆令子が３を選ぶ
和男が２を選べば全部とれる。令子負け。
ア…勝ち、イ…負け、ウ…負け

（２）
『１手目で令子が必ず勝つ』といえるには、１手目で令子が３枚取り、
２手目で和男が残りの２枚を同時に取れないと３手目で令子が勝つ。

ｎ＝５のとき、令子は１手目で４を選んで１・２・４の３枚を取ればいい。
和男は残りの３・５を同時に取れず、３手目で令子の勝利。
４

（３）①
説明問題。
１手目に令子が１・２を取る。２手目に和男が４を取る。
残りは〔３・５・６・７〕
令子が２枚取り、残りの２枚が同時に取れない組み合わせだと、
和男⇒令子で令子が勝つ。

令子が６を選んで３・６を取ると、残りの５・７を和男は２枚取れず、
令子が最後のカードをとることができる。
６

②
発想力が求められる。
令子の１手目終了後の残りは〔２・４・５・６・７〕
もし、２枚以上取れない組み合わせが連続すれば、
和男⇒令子⇒和男⇒令子⇒和男で和男の勝利。
２手目で和男が２を選ぶと、残りの〔４・５・６・７〕は１枚ずつしか取れない。
２

③
めんどい(´ﾟдﾟ｀)
時間が余った限り調べ尽くすしかない。

ただ、（２）で１手目に令子が４を選んで２手目に和男が６を選ぶと、
３手目に令子が何を選んでも和男が必ず勝つとあったから４は違う。
残り６分の１…。

消しやすいものから考えてみる。
１手目令子が最も約数の多い６を選ぶ。
残りは〔４・５・７〕でこれらは１枚ずつしか取れない。
和男⇒令子⇒和男で男の勝ち。×

１手目令子が５を選ぶ。
残りは〔２・３・４・６・７〕だが、２手目和男が６を選ぶと〔４・７〕
令子⇒和男で男の勝ち。×！

これと同じことが７にも言える。
５・７は素数であり、２と３と違って４・６を選んでも一緒に取れない。×！

今度は１手目令子が３を選ぶ。
前問と同じで２手目和男が２を選べば和男が勝つ。

２でも似たような現象が起こる。
残りは〔３・４・５・６・７〕で和男が３を選ぶと、
残りの４枚は１枚ずつしか取れなくなるから令子⇒和男⇒令子⇒和男で男の勝ち。

したがって、答えは１となる。
２手目で和男が選ぶ６パターンを調べてみると、適切な数字を選べば必ず令子が勝ちます。
１

2018年度　東京学芸大学附属小金井中学過去問【算数】大問４解説

問題ＰＤＦ 次のようなルールのゲームがあります。 〔ルール〕 ・２人組で行う。 ・１人ずつ交互に、１から順に数を言っていく。 ・１回に少なくとも１つ、（い）最大で３つまで数を言う。 ・（ろ）30を言ってしまったら負け。 〔例〕ＡさんとＢさん...

sabotensabo.com

2019.11.01

ルールは異なりますが、ゲームの必勝法を解明する問題がでました。
お時間がある方はどうぞです。