平均21.1点（前年比；＋2.1点）
100点―１人、０点―23人
問題はコチラ→ＰＤＦファイル
出題範囲の縮小は資料の活用（標本調査）。
大問１（小問集合）
（１）① 93.0％
２－（－５）－９
＝２＋５－９
＝－２
② 76.7％
（３ｘ－ｙ）/４－（ｘ＋２ｙ）/３
＝｛３（３ｘ－ｙ）－４（ｘ＋２ｙ）｝/12
＝（９ｘ－３ｙ－４ｘ－８ｙ）/12
＝（５ｘ－11ｙ）/12
③ 74.2％
ａ2ｂ×（－３ｂ）÷６ａｂ2
＝－ａ/２
④ 82.4％
12/√２－√32
＝６√２－４√２
＝２√２
（２） 71.6％
全体は50本、配った本数は７ａ本。
ｂ＝50－７ａ
（３） 33.1％！
ア：－１/２するので小さくなる。
イ：－と－は＋だから大きくなる。
ウ：ａは正の数。＋と－をかけるので－になる。
エ：＋を－で割って－になる。
ア・ウ・エ
（４） 50.4％
（ｘ－４）（ｘ＋２）＝３ｘ－２
ｘ2－２ｘ－８＝３ｘ－２
ｘ2－５ｘ－６
＝（ｘ＋１）（ｘ－６）＝０
ｘ＝－１、６
（５） 43.9％
ｙの変域に注目。
ｙ≧０だからグラフは下に凸でａ＞０。
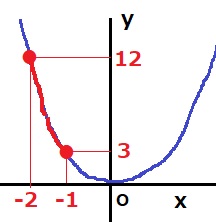
ｘ＝－１のとき、ｙ＝３
これをｙ＝ａｘ2に代入すると、
３＝１2ａ
ａ＝３
（６） 33.8％
高さをｈとする。アだけ底面の向きが違う点に注意！
ア：三角柱。底面は底辺６ｃｍ、高さ６ｃｍの三角形。
６×６÷２×ｈ＝18ｈｃｍ3
イ：円柱。底面は半径３ｃｍの円。
３×３×π×ｈ＝９πｈｃｍ3
ウ：四角錐。底面は１辺が６ｃｍの正方形。
６×６×ｈ÷３＝12ｈｃｍ3
π＝3.14…なので、イが最も大きい。
ウ＜ア＜イ
（７） 38.2％
40人の中央値（メジアン）は20番目と21番目の平均。
いずれも9.0～9.5秒の階級に含まれる。
相対度数は、10÷40＝0.25
（８） 28.7％！（部分点1.3％、無答19.9％）
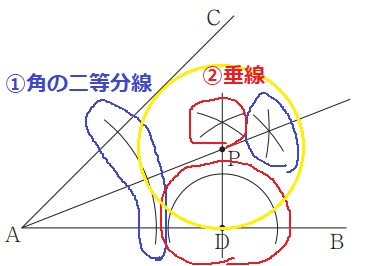
①円が２つの半直線に接する。
⇒円の中心は半直線ＡＢ、ＡＣから等距離（半径の長さ）にある。
⇒∠ＣＡＢの二等分線
②円は点Ｄで接する
⇒半径ＰＤと接線ＡＢは垂直に交わる。
⇒Ｄを通るＡＢの垂線
交点がＰである。
大問２（方程式）
（１） 67.4％
〔 あ 〕＝23
右辺が23だから、時間の合計で等式を立てている。
240ｘ＋75ｙ＝〔 い 〕
定数の4200がここで登場すると予測できる。
速さ×時間＝距離だから、ＡＰ間の距離とＰＢ間の距離を足して、
距離の合計で等式を立てる。
よって、ｘはＡＰ間の時間で、ｙはＰＢ間の時間を表している。
ウ
（２） 61.0％
１つ目は時間の合計で、ｘ＋ｙ＝23
２つ目は距離の合計で、420ｘ＋75ｙ＝4200
あ…ｘ＋ｙ、い…4200
（３） 55.0％
ｘ＋ｙ＝4200
右辺が距離の合計である4200ｍだから、
ｘはＡＰ間の距離、ｙはＰＢ間の距離を表す。
〔 う 〕＝23
23分は時間の合計。
時間＝距離÷速さなので、ｘ/240＋ｙ/75＝23
イ
大問３（数量変化）
（１） 43.1％
０≦ｘ≦５は直角三角形。
ｙ＝３×３÷２＝９/２
（２） 19.7％！（無答22.5％）
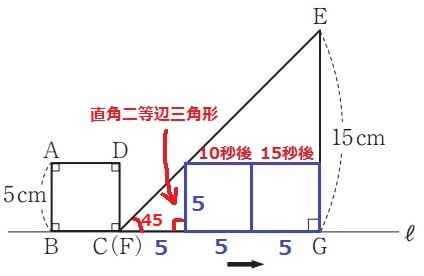
ｙの値が最大になる⇒正方形全体が直角三角形の中に入る。
Ｃの位置から10秒後～15秒後。
10≦ｘ≦15
（３） 2.6％!!（無答28.4％）
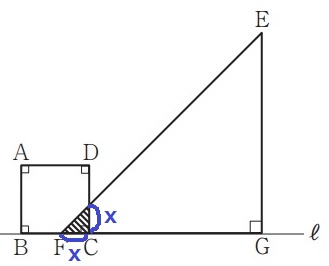
０≦ｘ≦５のときは、ｙ＝ｘ×ｘ×１/２＝１/２ｘ2
これにｙ＝８を代入。
８＝１/２ｘ2
ｘ＞０より、ｘ＝４
もう１つは、正方形が直角三角形からフェードアウトしていく15≦ｘ≦20。
直角三角形の外に出た部分の面積は、５×５－８＝17ｃｍ2
ＧＣ＝17÷５＝17/５ｃｍ
ｘ＝15＋17/５＝92/５
ｘ＝４、92/５
大問４（確率）
（１） 53.2％
１回目…６個の中から３個ある奇数を取り出す⇒３/６
２回目…残りの５個から２個ある奇数を取り出す⇒２/５
３/６×２/５＝１/５
（２） 27.1％！
ｍ2＞４ｎ
サボはｍ2で場合分けしました。
◆ｍ2＝１
これより小さい４ｎはない。
◆ｍ2＝４
同様に無い。
◆ｍ2＝９
ｎ＝１、２
◆ｍ2＝16
ｎ＝１～３
◆ｍ2＝25
ｎ＝１～６
◆ｍ2＝36
ｎ＝１～６
全部で17通り。確率は17/36。
大問５（関数）
（１） 71.3％
ｙ＝６/ｘにｘ＝２を放り込む。
ｙ＝６/２＝３
（２） 7.5％！（無答27.4％）
△ＡＯＢのどこが直角になりうるか。
Ａはｙ＝６/ｘ上の点。
反比例はｙ軸と交わらないので、∠ＡＯＢは直角にならない。
ＡＯ＝ＡＢから∠ＡＢＯも直角にならない。
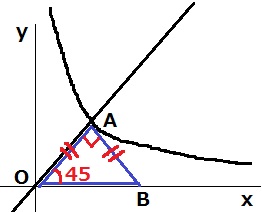
となると、∠ＯＡＢ＝90°しかない。
∠ＡＯＢ＝45°ゆえ、ｙ＝ｘ
（３） 1.6％!!!（部分点0.8％、無答53.2％！）
説明問題。
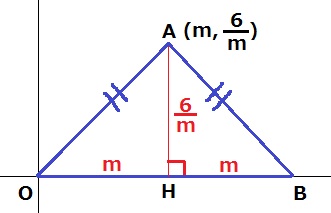
ｙ＝６/ｘから、Ａ（ｍ、６/ｍ）
ＡからＯＢに垂線。
交点をＨとすると、△ＡＯＢは二等辺三角形だからＨはＯＢの中点。
底辺ＯＢは２ｍ、高さＡＨは６/ｍ。
△ＡＯＢの面積は、２ｍ×６/ｍ÷２＝６
計算結果が変数を含まない定数。
したがって、ｍがどんな値であっても、△ＡＯＢの面積は６で一定である。
大問６（平面図形）
（１） 6.4％!!（部分点25.1％、無答25.6％）
△ＡＥＣ∽△ＤＥＢの証明。
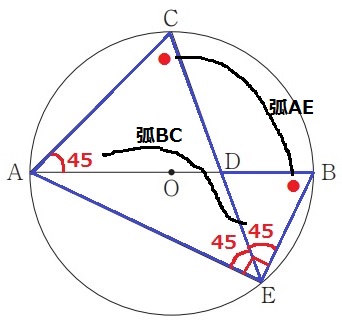
弧ＡＥの円周角で、∠ＡＣＥ＝∠ＤＢＥ
弧ＢＣの円周角で、∠ＣＡＢ＝∠ＤＥＢ＝45°
直径ＡＢに対する円周角で、∠ＡＥＢ＝90°
∠ＡＥＣ＝90－45＝45°
∠ＡＥＣ＝∠ＤＥＢ＝45°
２角が等しく、∽。
（２）① 28.9％！（無答17.3％）
ＣＯに補助線。
半径より、ＯＡ＝ＯＣ
∠ＣＡＯ＝45°であるから、△ＡＣＯは直角二等辺三角形。
辺の比は１：１：√２→ＡＣ＝６√２ｃｍ
② 0.2％!!!（無答28.2％）
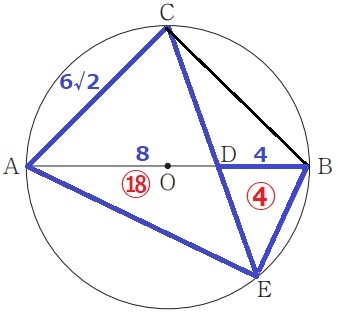
ＡＤ＝６＋２＝８
ＤＢ＝６－２＝４
前問の相似を利用する。
ＡＣ：ＤＢ＝６√２：４＝３√２：２
面積比は辺の比の２乗だから、
△ＡＥＣ：△ＤＥＢ＝⑱：④
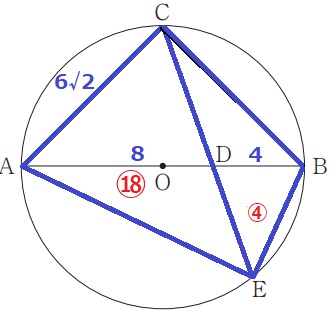
ここから四角形ＡＥＢＣの面積比を求める。
△ＡＥＣと△ＢＥＣの底辺をＣＥとすると、
高さはの比はＡＤ：ＤＢ＝８：４＝２：１
→△ＡＥＣと△ＢＥＣの面積比は２：１
→△ＡＥＣと四角形ＡＥＢＣの面積比は２：３
四角形ＡＥＢＣの面積は、⑱×３/２＝㉗
四角形ＡＥＢＣの面積は△ＤＥＢの27/４倍。
大問１
（３）ａに具体的な正の数を当てはめてもよい。
（５）ｙ≧０に注目してａ＞０を先に確定する。
（６）アだけ横向きである。
大問２
文章題は線分図や表で情報整理することをオススメします。
大問３
（２）正方形がスッポリ入るタイミングを調べる。
調査に時間を要しないレベルだが無答率がやや高い。
（３）正方形が入っていく途中と出て行く途中である。
よくある出題形式で、計算も複雑ではないが正答率が低い！
大問４
（２）ひたすら調べていくしかない。
大問５
（２）急に正答率が落ちる。どこが直角になるかが勝負。
（３）Ａ座標をｍで表す⇒△ＡＯＢの面積もｍで表そうと試みる。
すると変数ｍが消え、値は定数だから面積は一定である。
難しい流れではないと思う。
大問６
（１）２角相等は見当がつく。45°は計算で出す。
数値が与えられたときは計算を想定する。
（２）②45°から有名三角形を探さなくても解ける。
ＣＥが内接四角形ＡＥＢＣの対角線であることから、
△ＡＥＣの面積比さえ出せれば四角形ＡＥＢＣもわかる。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント