2022年度　福井県公立高校入試・選択問題Ｂ過去問【数学】解説

平均55.5点（前年比；＋6.3点）
問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）ア
12ｘｙ÷６ｙ×（－３ｘ）
＝－６ｘ²

イ
２/３ａ－（ａ－ｂ）/２　←６で通分
＝｛２×２ａ－３（ａ－ｂ）｝/６
＝（ａ＋３ｂ）/６

（２）
３ａｘ²＋12ａｘ＋９ａ　←共通因数３ａ
＝３ａ（ｘ²＋４ｘ＋３）
＝３ａ（ｘ＋１）（ｘ＋３）

（３）
３ｘ²＋３ｘ－１＝０
解の公式を適用して、ｘ＝（－３±√21）/６

（４）
千の位と一の位をｘ、百の位と十の位をｙとすると、
４桁の整数は1000ｘ＋100ｙ＋10ｙ＋ｘと表せる。
1000ｘ＋100ｙ＋10ｙ＋ｘ
＝1001ｘ＋110ｙ
＝11（91ｘ＋10ｙ）
91ｘ＋10ｙは整数なので、11（91ｘ＋10ｙ）は11の倍数である。
したがって、千の位と一の位の数が等しく、百の位と十の位の数が等しい数は11の倍数である。

（５）

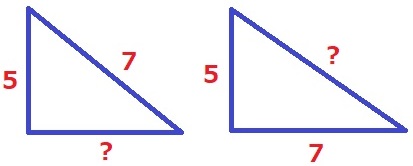
他の辺を？とする。
直角三角形の斜辺は最も長い辺なので、斜辺は７か？の２通りである。
√（７²－５²）＝２√６ｃｍ
√（５²＋７²）＝√74ｃｍ
２√６ｃｍ、√74ｃｍ

（６）
答案では説明も書く。
平均３冊から、ａ＋ｂの和を求める。
３×10－（２＋４＋１＋１＋６＋５＋４＋２）
＝30－25＝５冊
（ａ、ｂ）＝（０、５）（１、４）（２、３）の３通りが考えられる。
10個の中央値（メジアン）は５番目と６番目の平均で、これが３冊になる組み合わせは、
（ａ、ｂ）＝（０、５）（１、４）

（７）

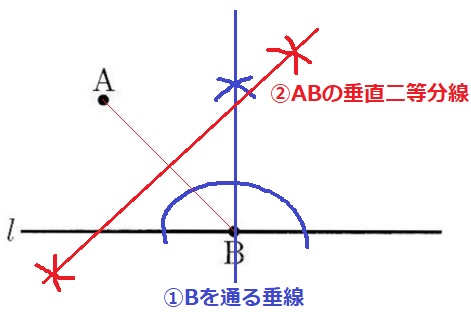
円は直線ｌと点Ｂで接する。半径と接線は接点Ｂで直交する。
また、ＡとＢは円周上の２点で、半径ＯＡ＝ＯＢとなるからＯはＡとＢから等距離にある。
→ＡＢの垂直二等分線はＡ、Ｂから等距離にある点の集合で、これのどこかにＯがある。
①Ｂを通る垂線と②ＡＢの垂直二等分線の交点が円の中心Ｏ。

大問２（確率）

（１）ア
全体は３×３＝９通り
積が６となる組み合わせは（ａ、ｂ）＝（２、３）（６、１）の２通り。
確率は２/９

イ
120を素因数分解すると、120＝２³×３×５
ａ（２・４・６）
ｂ（１・３・５）
パッと見た感じ、120/ａｂのほとんどが割り切れて自然数になる。
ｂ＝１ならば、ａは何でもいい。
ｂ＝５でも同様。
しかし、３の素因数は１つしかないので、ｂ＝３のとき、ａ＝６だけは無理。
残りの８通りはＯＫなので、確率は８/９。

（２）
確率１ということは、（ａ、ｂ）の組み合わせが何であっても120/ａｂが自然数になる。
前問より（ａ、ｂ）＝（６、３）のときだけダメなので、Ｂの３を何かと入れ替える。
ａ＝６だとすると、ｂの最大数は120÷６＝20…と答えたくなるが、
仮にｂを20に入れ替えると、ａ＝４のとき、120÷20÷４が割り切れない！

ａ＝４のとき、ｂの最大数は120÷４＝30＝２×３×５
ａ＝６のとき、ｂの最大数は120÷６＝20＝２²×５
共通する因数から、ｂの最大数は２×５＝10
ア…３、イ…10

＠別解＠
ａの数を２・４・６の最小公倍数12とする。
ｂの最大数は、120÷12＝10

大問３（方程式）

（１）
問題文の情報を図であらわす。

ＡとＢのあいだは、100－（ｘ＋ｙ）ｋｍ。

（２）ア

１つ目は【学校～Ａ＋Ｂ～目的地】の時間で等式を立てる。
全体は90分＝３/２時間
時間は全体の５/９倍だから、３/２×５/９＝５/６時間
道のり÷速さ＝時間
ｘ/50＋ｙ/45＝５/６　…①

２つ目は【Ａ～Ｂ】で等式を立てる。
時間は３/２×４/９＝２/３時間
先ほどのように道のり÷速さ＝時間で、｛100－（ｘ＋ｙ）｝/90＝２/３としても良いが、
速さと時間が確定しているから、ＡＢ間の道のりは90×２/３＝60ｋｍとわかる。
ということは、それ以外の【学校～Ａ＋Ｂ～目的地】の道のりが100－60＝40ｋｍ
道のりで等式を立てると、ｘ＋ｙ＝40　…②
（例）
ｘ/50＋ｙ/45＝３/２×５/９
ｘ＋ｙ＝100－90×（３/２×４/９）
（*どの程度まで式を加工すべきか判断に迷う。理屈があっていれば間違いにはならない）

イ
ｘ/50＋ｙ/45＝５/６　…①
ｘ＋ｙ＝40　…②

①を450倍して、９ｘ＋10ｙ＝375　…③
③－②×９をすると、ｙ＝15
②に代入して、ｘ＝40－15＝25
ｘ＝25、ｙ＝15

大問４（関数）

（１）

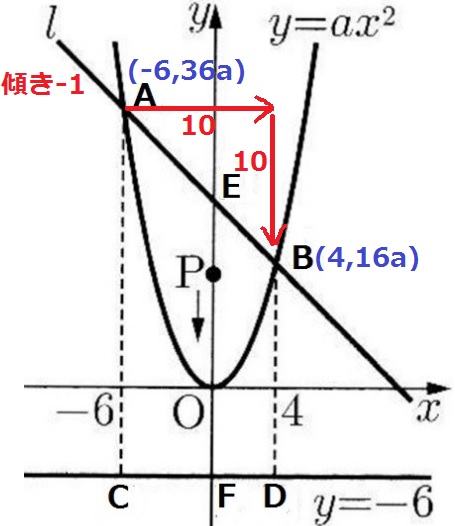
ｙ＝ａｘ²にｘ座標を代入すると、Ａ（－６、36ａ）Ｂ（４、16ａ）
直線ｌの傾きは－１。
Ａ⇒Ｂは右に10、下に10移動する。
ＡとＢのｙ座標で等式。
36ａ－16ａ＝10
ａ＝１/２

（２）
前問のａに代入して座標を確定する。
Ａ（－６、18）Ｂ（４、８）
Ａから左に６、下に６移動して、切片は18－６＝12
ｙ＝－ｘ＋12

（３）ア
△ＰＢＡの幅は10ｃｍ、高さはＥＰ＝ｔｃｍなので、
△ＰＢＡの面積は、10×ｔ÷２＝５ｔｃｍ²

イ
答案では説明も記述する。
△ＰＢＡ＝５ｔとわかったので、△ＰＣＤの面積もｔで表してみる。

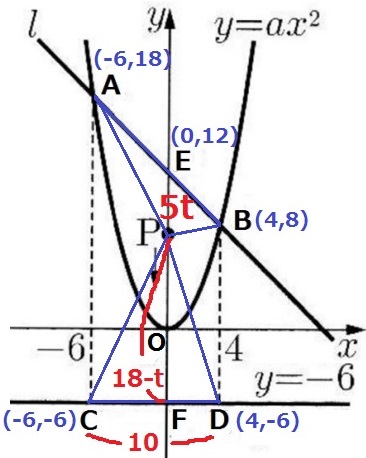
座標を確認。
底辺ＣＤ＝10ｃｍ、高さＰＦ＝ＥＦ－ＥＰ＝18－ｔｃｍ
△ＰＣＤの面積は、10×（18－ｔ）÷２＝90－５ｔｃｍ²
△ＰＢＡ＋△ＰＣＤ＝５ｔ＋（90－５ｔ）＝90ｃｍ²
ｔの値に関係なく、90ｃｍ²で一定である。

＠別解＠

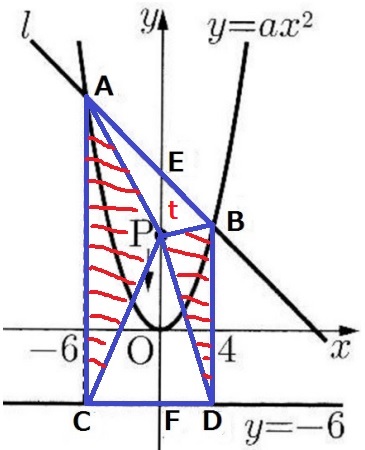
△ＰＢＡ＋△ＰＣＤ＝四角形ＡＣＤＢ－（△ＰＡＣ＋△ＰＢＤ）
ＰがＥ⇒Ｆに移動しても等積変形で△ＰＡＣと△ＰＢＤの面積は変わらないから、
△ＰＢＡ＋△ＰＣＤは一定である。

（４）

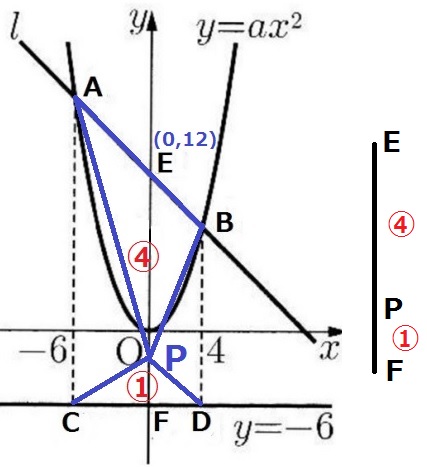
２つの三角形の面積の和は一定。
底辺もともに一定で、各々の高さだけが変動する。
→高さの比が４：１であれば、面積比も４：１。
ＥＰ：ＰＦ＝④：①
ＥＦ＝18ｃｍでＰの速さは毎秒１ｃｍだから、18×④/⑤÷１＝72/５秒後

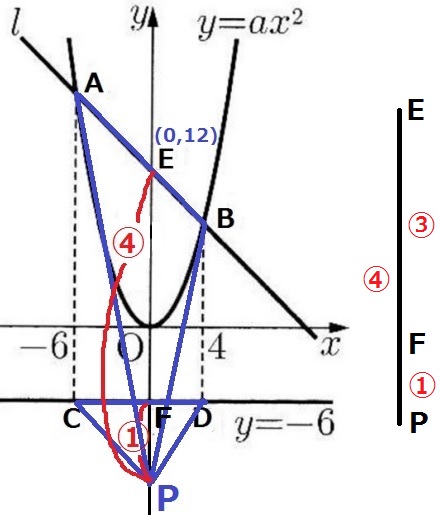
もう１つはＰがＦを通り越した場合。
ＥＰ：ＦＰ＝④：①
ＥＦ＝③＝18だから、18×④/③÷１＝24秒後
72/５秒後、24秒後

大問５（平面図形）

（１）
△ＡＢＤ∽△ＤＣＦの証明。

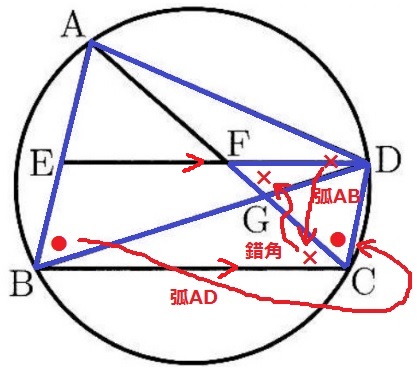
弧ＡＤに対する円周角（●）
弧ＡＢに対する円周角→ＥＤ//ＢＣの錯角（×）
２角が等しいので∽

（２）

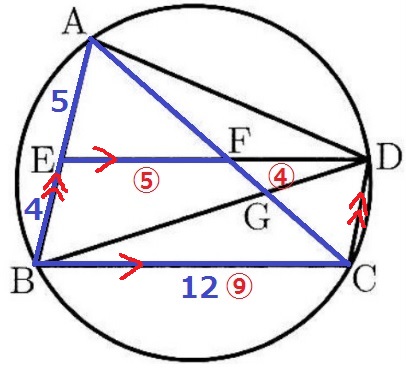
△ＡＥＦ∽△ＡＢＣより、ＥＦ：ＢＣ＝ＡＥ：ＡＢ＝⑤：⑨
平行四辺形ＥＢＣＤの対辺は等しいので、ＥＤ＝⑨
ＤＦ＝⑨－⑤＝④
ＤＦ＝12×④/⑨＝16/３ｃｍ

ＡＤは△ＡＢＤの１辺→（１）△ＡＢＤ∽△ＤＣＦを活用する。
平行四辺形の対辺から、ＤＣ＝ＥＢ＝４ｃｍ
相似比は△ＡＢＤ：△ＤＣＦ＝⑨：④
ＡＤ＝16/３×⑨/④＝12ｃｍ
ＤＦ＝16/３ｃｍ、ＡＤ＝12ｃｍ

（３）

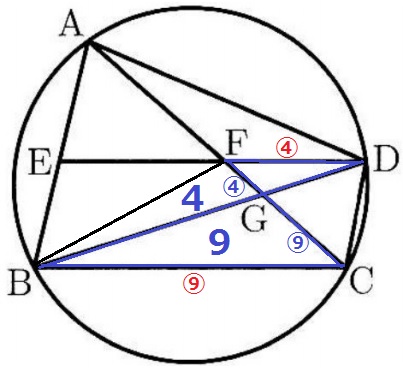
（２）より、ＦＤ：ＢＣ＝④：⑨
△ＦＤＧ∽△ＣＢＧより、ＦＧ：ＧＣ＝④：⑨
→△ＢＦＧ：△ＢＧＣ＝４：９
△ＢＣＦ＝13、平行四辺形ＢＣＤＥ＝13×２＝26
四角形ＢＣＤＥ（Ｓ）：△ＢＦＧ（Ｔ）
＝26：４＝13：２