2023年度　山梨県公立高校入試問題過去問【数学】解説

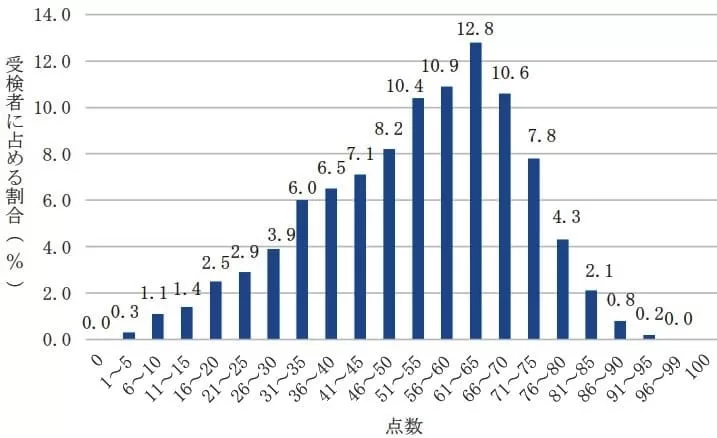
平均52.8点（前年比；－2.0点）
最高点：93点、最低点：０点

問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）　94％
６－（－７）
＝６＋７
＝13

（２）　94％
14÷（－７/２）
＝14×（－２/７）
＝－４

（３）　93％
－２²＋（－５）²
＝－４＋25
＝21

（４）　70％
√８－３√６×√３
＝２√２－９√２
＝－７√２

（５）　73％
９ｘ²ｙ×４ｘ÷（－８ｘｙ）
＝－９/２ｘ²

（６）　85％
ｘ（３ｘ＋４）－３（ｘ²＋９）
＝３ｘ²＋４ｘ－３ｘ²－27
＝４ｘ－27

大問２（小問集合）

（１）　75％
ｘ²－９ｘ－36
＝（ｘ＋３）（ｘ－12）＝０
ｘ＝－３、12

（２）　58％

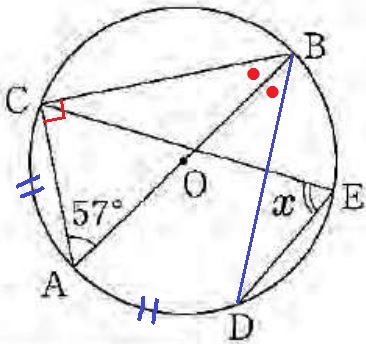
ｘは弧ＣＤに対する円周角。
ＢＤに補助線、∠ＣＢＤを求めればいい。
直径に対する円周角から∠ＡＣＢ＝90
∠ＣＢＡ＝180－（90＋57）＝33°
弧ＡＣ＝弧ＡＤより、∠ＣＢＡ＝∠ＤＢＡ（●）
ｘ＝33×２＝66°

（３）　72％
反比例の比例定数はｘとｙの積。
４×（－５）＝－20

（４）　45％（部分正答17％）

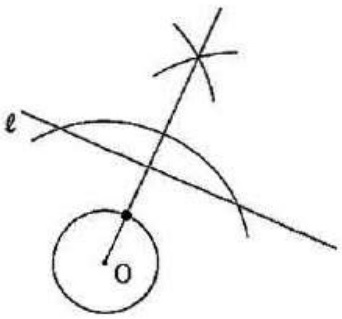
直線ℓに最も近い、円Ｏの円周上にある点の作図。
Ｏを通る直線ℓの垂線を作図し、直線ℓ側の円周との交点が答え。

（５）①　74％
四分位範囲＝第３四分位数－第１四分位数
130－80＝50冊

②　63％
箱ひげ図を描く。

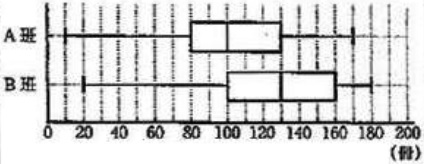
最小値20冊、最大値180冊。
15人の中央値（第２四分位数）は８番目の130冊。
第１四分位数は下位７人の真ん中、下から４番目の100冊。
第３四分位数は上位７人の真ん中、上から４番目の160冊。

大問３（方程式＆確率）

（１）①　54％
イスがｘ個。
通路沿いの両端にイスがあり、（ｘ－１）はイスとイスの間の個数。
ウ

②記号：72％、説明：32％！（部分正答20％）
答案では説明も記述する。
0.5ｘ＋1.5（ｘ－１）＋２ｙにｘ＝12、ｙ＝3.5を代入する。
0.5×12＋1.5（12－１）＋２×3.5
＝６＋16.5＋７
＝29.5＞29
29ｍを超えるので、できない。
イ

（２）①　68％
６人から２人選ぶ→₆Ｃ₂＝15通り

②　58％（部分正答９％）
Ａが選ばれない確率は６人中４人。
続けて、Ｂが選ばれない確率は残りの５人中３人。
４/６×３/５＝２/５

大問４（数量変化）

（１）　60％（部分正答14％）
５分後の姉と弟の道のりの差を説明する。
ｘ＝５のときの姉（グラフ①）と弟（グラフ②）のｙ座標の差を求める。

（２）　60％
②の０≦ｘ≦10は（10、800）を通る比例。
ｙ＝80ｘ

（３）花屋：44％、ケーキ屋：49％

姉は自宅から花屋までの片道2400ｍを10分で移動している。
もし、花屋からとんぼ返りしたら往復で20分。
実際に自宅へ到着したのは35分後だから、２つの店で合計15分間滞在していた。

花屋～ケーキ屋の移動時間は、10×960/2400＝４分
花屋の出発時刻は10：26の４分前である10：22。
花屋の滞在時間は、10：22－10：10＝12分間
ケーキ屋の滞在時間は、15－12＝３分間
花屋…12分間、ケーキ屋…３分間

（４）　15％！
中学受験の戦法を使います。

最初の10分で姉は弟の３倍の距離を移動している。
速さの比は、姉：弟＝３：１
距離一定の場合、時間の比は逆比で姉：弟＝①：③

ラスト５分を拾い上げる。
姉が弟に追いついた地点から自宅まで、姉は①の時間、弟は③の時間がかかる。
②＝５分だから、弟の時間は５×③/②＝15/２分
弟の速さは分速80ｍなので、80×15/２＝600ｍ

大問５（関数＆平面図形）

（１）①　50％
ｙ＝１/４ｘ²にそれぞれのｘ座標を代入。
Ａ（－６、９）→Ｂ（４、４）
右に10、下に５だから、傾きは－５/10＝－１/２
Ｂから右に４、上に２移動して、切片は４＋２＝６
ｙ＝－１/２ｘ＋６

②　５％!!（部分正答０％）

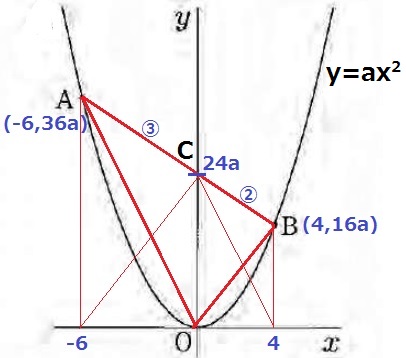
各座標をａで表すと、Ａ（－６、36ａ）Ｂ（４、16ａ）
ＡＢの切片をＣとする。
ｘ座標の差より、ＡＣ：ＣＢ＝６：４＝③：②
Ｃのｙ座標は、16ａ＋（36ａ－16ａ）×②/⑤＝24ａ
（内分点の公式を知っている人は、（36ａ×②＋16ａ×③）/（③＋②）＝24ａ）
△ＯＡＢは底辺10、高さ24ａの三角形だから、
10×24ａ÷２＝20
ａ＝１/６

（２）①　16％！（部分正答52％）
△ＡＢＤ∽△ＢＣＤの証明。

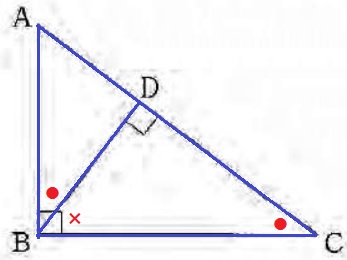
∠ＡＤＢ＝∠ＢＤＣ＝90°
∠ＡＢＤ（●）＝90°－∠ＤＢＣ（×）
△ＢＤＣの内角で、∠ＢＣＤ＝180－（90＋×）＝90－×＝●
２角相等で∽。

②Ｘ：74％、Ｙ：82％

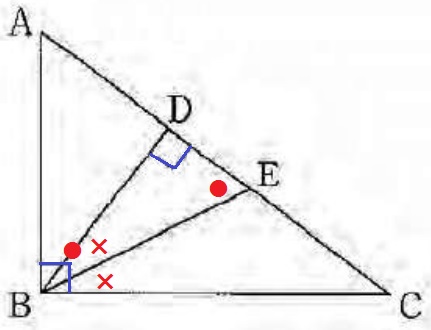
∠ＡＢＥ（●）＋∠ＥＢＣ（×）＝90°
仮定より、∠ＥＢＣ＝∠ＤＢＥ（×）
直角三角形ＤＢＥの内角より、∠ＤＥＢ＋∠ＤＢＥ（×）＝90°だから、
∠ＤＥＢ（∠ＡＥＢ）＝●
△ＡＢＥは２つの角が等しい→二等辺三角形
ＡＢ＝ＡＥ
Ｘ…エ、Ｙ…カ

③　２％!!（部分正答０％）

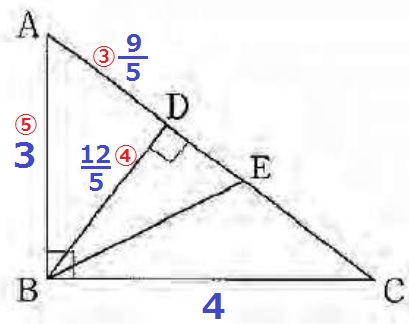
ＡＢ：ＢＣ＝３：４から、△ＡＢＣの辺の比は３：４：５。
△ＡＢＣ∽△ＡＤＢより、△ＡＤＢも同様に３：４：５。
ＡＤ＝３×③/⑤＝９/５ｃｍ
ＢＤ＝３×④/⑤＝12/５ｃｍ

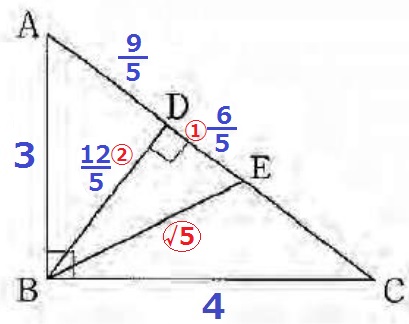
前問より、ＡＥ＝ＡＢ＝３ｃｍだから、ＤＥ＝３－９/５＝６/５ｃｍ
△ＢＥＤで三平方。ＢＤ：ＤＥ＝②：①なので、ＢＥ＝〇√５
ＢＥ＝６/５×〇√５＝６√５/５ｃｍ

大問６（空間図形）

（１）　39％（部分正答０％）
△ＡＢＣは辺の比が１：１：√２の直角二等辺三角形。
対角線ＡＣ＝８√２ｃｍ

（２）①　14％！

ＡＣで区切る。
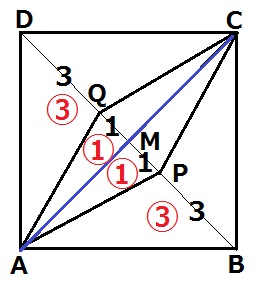
△ＤＡＣ：△ＱＡＣ＝ＤＭ：ＱＭ＝④：①
対称性から、△ＢＡＣ：△ＰＡＣ＝④：①で、
全体で合わせると、四角形ＡＰＣＱは正方形ＡＢＣＤの１/４。
 
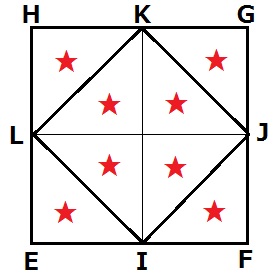
★は同じ面積。
四角形ＬＩＪＫは正方形ＥＦＧＨの１/２。
正方形ＡＢＣＤと正方形ＥＦＧＨは同じ面積だから、
四角形ＡＰＣＱ：四角形ＬＩＪＫ＝１/４：１/２＝１：２

②　４％!!

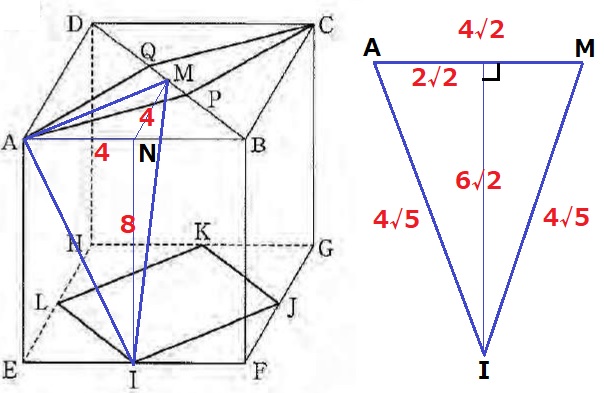
ＡＢの中点をＮとする。
△ＡＮＭは辺の比が１：１：√２の直角二等辺→ＡＭ＝４√２ｃｍ
△ＡＩＮで三平方→辺の比は１：２：√５で、ＡＩ＝４√５ｃｍ
また、△ＡＩＮと△ＭＩＮは共通辺ＮＩ、ＡＮ＝ＭＮ、∠ＡＮＩ＝∠ＭＮＩ＝90°より、
２辺とあいだの角が等しく合同。
ＡＩ＝ＭＩで、△ＡＩＭは二等辺三角形。高さを三平方でだすと６√２ｃｍ。
△ＡＩＭの面積は、４√２×６√２÷２＝24ｃｍ²

＠別解＠

三角錘Ｉ―ＡＮＭはＡＮ：ＭＮ：ＮＩ＝１：１：２、∠ＡＮＭ＝∠ＡＮＩ＝∠ＭＮＩ＝90°
中学受験にでてくる有名錘で、これを展開すると正方形になる。
△ＡＩＭの面積は、８×８－（４×４÷２＋８×４÷２×２）＝24ｃｍ²

③　０％!!!（部分正答０％）

あれこれ試行錯誤してみたのですが、そのまま断頭三角柱で求積するのが良いと思いました。
ＬＩとＫＪの中点をそれぞれＲ、Ｓとする。
四角錘Ａ―ＰＱＬＩ…底面積は△ＡＲＭ、高さはＡ、ＩＬ、ＰＱの平均。
四角錘Ｃ―ＰＱＫＪ…対称性から、四角錘Ａ―ＰＱＬＩと等積。
立体ＰＱ―ＬＩＪＫ…底面積は△ＭＲＳ、高さはＰＱ、ＩＬ、ＪＫの平均。

ＡＭ＝ＡＣ÷２＝８√２÷２＝４√２ｃｍ
ＰＱ＝ＢＤ÷４＝８√２÷４＝２√２ｃｍ
四角錘Ａ―ＰＱＬＩ×２＋立体ＰＱ―ＬＩＪＫ
＝４√２×８÷２×（０＋４√２＋２√２）/３×２＋４√２×８÷２×（２√２＋４√２＋４√２）/３
＝128＋320/３
＝704/３ｃｍ³