平均22.39点(前年比;-3.00点)

問題はこちら→東進ハイスクールさん(解答)
出題範囲の除外はなし。
大問1(計算)
(1)ア 96.4%
18÷(-6)-9
=-3-9
=-12
イ 85.2%
(-2a)2×÷8a×6b
=4a2÷8a×6b
=3ab
ウ 86.4%
(4x-y)/7-(x+2y)/3
={3(4x-y)-7(x+2y)}/21
=(12x-3y-7x-14y)/21
=(5x-17y)/21
エ 79.8%
(√5+√3)2-9√15
=5+2√15+3-9√15
=8-7√15
(2) 83.9%
16a2-b
=(4a+b)(4a-b)
=(4×11+43)(4×11-43)
=87×1
=87
(3) 87.6%
(x-2)(x-3)=38-x
x2-5x+6=38-x
x2-4x-32
=(x+4)(x-8)=0
x=-4、8
大問2(小問集合)
(1) 72.0%
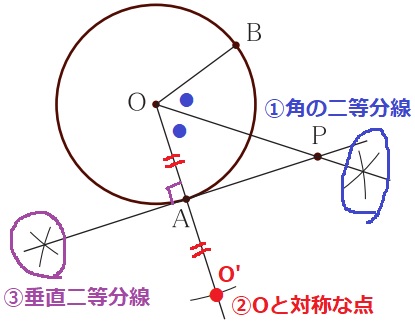
∠AOP=∠BOP→∠AOBの二等分線
半径と接線は直交するので、∠OAP=90°をつくりたい。
OAを延長してAを通る垂線上にPがある。
①∠AOBの二等分線。
②OAを延長。OAの長さをとり、Aに針を合わせてO’を作る。
OとO’は垂線に対して対称にある点(対応する点)
③OO’の垂直二等分線。①との交点がP。
(2)ア 28.1%!
小さい方からa番目の数…a
大きい方からb番目の数…1番目が14、2番目が13、3番目が12、b番目は15-b。
a+(15-b)
=a-b+15
*誤答はa-b+14が目立つ。
イ 30.2%!
7と8の正六角形は必ず残る。
◆丸だけをなくす
〇は全部取るので3以上…4通り
□は1枚以上残すので5未満…4通り
4×4=16通り
◆四角だけをなくす
〇は1枚以上残すので3未満…2通り
□は全部取るので5以上…2通り
2×2=4通り
計20通り、確率は20/36=5/9
*誤答は1/2や7/12などがみられる。
大問3(データの活用)
(1) 40.8%
それぞれの値を書いておこう。
ア・イ・ウ・エ
最大値…85・75・55・65
中央値…65・45・35・55
(*便宜上、最大値は階級値で示した。
30人の中央値は15番目と16番目の平均)
『最大値は2組の方が大きい』『中央値は1組の方が大きい』
アは最大値、中央値ともに最大だから、1組でも2組でもない。
ウは最大値、中央値ともに最小で、1組でも2組でもない。
残りのイ・エで中央値が大きいエが1組、最大値が大きいイが2組。
3年1組…エ、3年2組…イ
*誤答は1組エ、2組アが目立つ。
(2) 31.7%!

面積図で表す。
上位10位を均すと高さが62.9cm、60人全員を均すと高さが45.4cmの長方形。
?が残り50人の平均値。
45.4より上の部分と下の部分を均して45.4になるから、赤い部分の面積が等しい。

左上の長方形は、(62.9-45.4)×10=175
右上の長方形の高さは、175÷50=3.5cm
残り50人の平均値は、45.4-3.5=41.9cm
*誤答は17.5などが見られた。62.9-45.4=17.5?
大問4(方程式)
19.5%!
説明問題。表を使って情報を整理しよう。
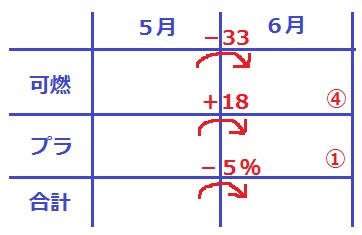
可燃が33kg減少、プラは18kg増加、合計は5%減少。
6月の可燃はプラの4倍であった。
6月のプラをxとすると、いろんなところがxで表せそう。

合計で等式を立てる。
(5x+15)×95/100=5x
95x+285=100x
x=57
4x=57×4=228
6月の可燃ごみ…228kg、6月のプラスチックごみ…57kg
*正答率が低い。数量関係の正しい立式ができていないものが多い。
また、どのような数量をxやyで表しているのかを明記していないものもみられる。
大問5(空間図形)
(1) 77.0%

底面BCDと辺ADが垂直なので、直角は∠ADB、∠ADC
(2) 11.3%!
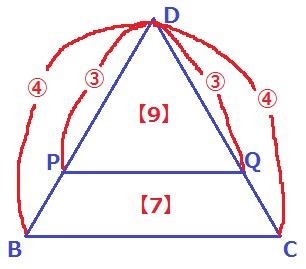
正三角形DBCと正三角形DPQの相似比は、12:9=④:③
△DBCの面積…④×④=【16】
△DPQの面積…③×③=【9】
四角形BCQPの面積…【16】-【9】=【7】
四角形BCQPは△BCDの7/16倍。
*相似比と面積比の関係を正しく捉えていないための誤答が目立つ。
(3) 2.0%!!
手早く処理するには経験を積むしかない。
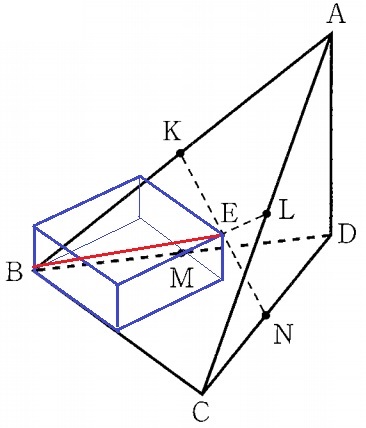
斜め線を求めるとき、それを対角線とする直方体をイメージする。
BEを対角線とする青い直方体の縦×横×高さを調べる。

直方体の頂点をF、Gとする。
K・L・M・Nは各々の辺の中点で、EはKN、LMの中点。
三角錐を上から眺めると、Eを中心にK・LとM・Nは左右対称にある。
底面の正三角形DBCにおいて、Eの真下にあるGはMNの中点にあり、
右図のようにDから底辺BCに垂線をひくと、GとFを通過する。
BF=12÷2=6cm
△DBFの内角は30°-60°-90°で辺の比は1:2:√3→GF=6√3÷2=3√3cm
AD=8cm
△ACD∽△LCN→LN=8÷2=4cm
△LMN∽△EMG=EG=4÷2=2cm
【辺の長さがa、b、cの直方体の対角線の長さ→√(a2+b2+c2)】
BE=√{62+(3√3)2+22}
=√67cm
*正答率が低く、無答も多い。
大問6(関数)
(1) 78.5%
y=-1/2x2は上に凸のグラフ。
x=0のとき、最大値y=0
x=2のとき、最小値y=-1/2×22=-2
-2≦y≦0
(2) 67.5%
y=-1/2x2にx=4を代入。
y=-1/2×42=-8
D(4、-8)
Eはy軸についてDを対称移動させた点。
E(-4、-8)
*誤答では(4、-8)が目立つ。
(3) 14.5%!
解答では求める過程も記述する。

AからBに移動するには右に7、上に7a→傾きはa
Aから右に3、上に3a移動。9a+3a=12a
G(0、12a)
OからAに移動するには左に3、上に9a。
B(4、16a)から左に3、上に9a移動してF(1、25a)
FCの傾き…(0-25a)÷(4-1)=-25/3a
GDの傾き…(-8-12a)÷(4-0)=-3a-2
FC//GDゆえ、-25/3a=-3a-2
a=3/8
*問題を解くのに必要な点座標を正しく求められないための誤答が目立ち、無答も多い。
大問7(平面図形)
(1) 22.8%!
△BOE≡△DOGの証明。
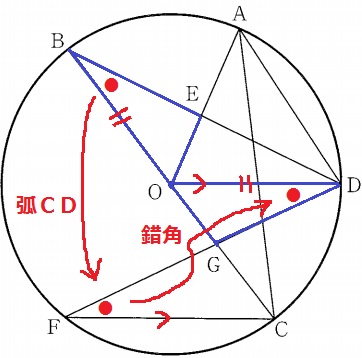
半径より、BO=DO
弧CDに対する円周角とOD//FCの錯角で、∠OBE=∠ODG
問題はもう1つの等角…。
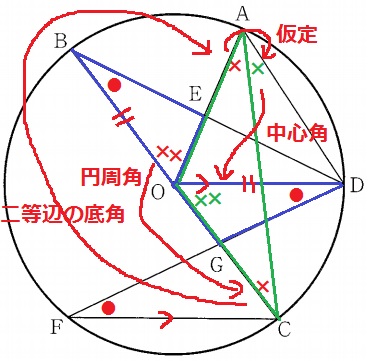
ポイントは半径OC=OAから、△OCAが二等辺三角形であること。
∠BOE=××とする。
弧ABに対する円周角∠ACB=×
二等辺三角形OCAの底角∠OAC=×
仮定より、∠CAD=×
弧CDに対する中心角∠DOG=××
∠BOE=∠DOG=××
以上、1辺と両端角が等しく合同。
*OB=OD、∠OBE=∠ODGは説明されているが、もう1組の対応する角が等しい理由について、
論理の飛躍をしているものや説明不十分なものが目立つ。
(2) 7.4%!!
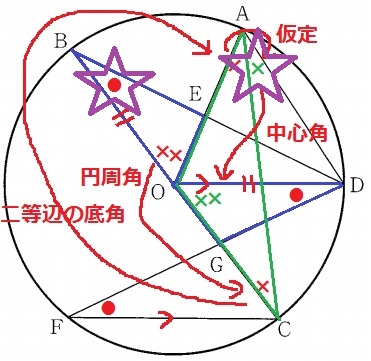
先ほどの図を観察すると、弧CDに対する円周角から∠CBD=∠CAD
つまり、●と×は同じ角度である。
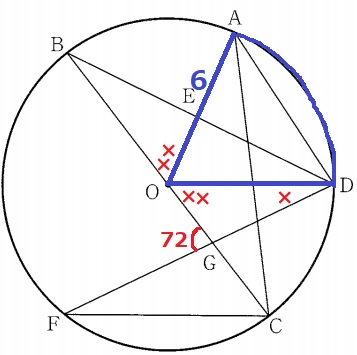
中心角∠AODさえわかれば、弧ADの長さがでる。
△ODGで外角定理→×××=72°
前問の証明より、∠BOE=∠DOG
∠BOE+∠DOG=××××=72×4/3=96°
∠AOD=180-96=84°
弧ADの長さは、6×2×π×84/360=14/5πcm
*誤答では2πなどがみられる。無答も多い。
●講評●
大問1
死守。
大問2
(2)良い問題だと思う。
正六角形は必ず残るので、〇を残すか□を残すかで場合分け。
大問3
(1)推論を含む。少し焦るが、落ち着いて対処しよう。
(2)平均。解説では面積図を利用した。
大問4
表で情報整理をする。内容があっていれば別の式でも良い。
大問5
(3)大問7まであるので、なるべく時間をかけたくない。
無理そうであれば後回し推奨。
真上から見た図、正面から見た図をイメージする。
大問6
(3)変化の割合からG座標を算出。
2直線の傾きの処理。時間をかけ過ぎないようにしたい。
大問7
(1)記述が大変(´゚д゚`)
△OCDが二等辺であることを掴まないと繋げられない。
(2)前問の角度を利用するので、(1)を間違えると立て続けに間違える。



コメント