2023年度　広島県公立高校入試問題過去問【数学】解説

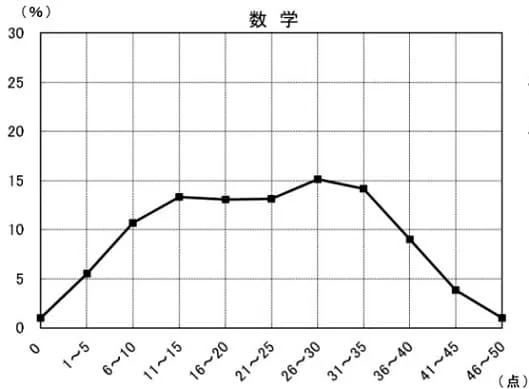
平均22.6点（前年比；＋2.4点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）　91.3％
－８－（－２）＋３
＝－８＋２＋３
＝－３

（２）　95.2％（部分正答0.1％）
28ｘ²÷７ｘ
＝４ｘ

（３）　81.0％（部分正答0.2％）
√50－６/√２
＝５√２－３√２
＝２√２

（４）　74.8％（部分正答0.1％）
（ｘ－６ｙ）²
＝ｘ²－12ｘｙ＋36ｙ²

（５）　71.4％（部分正答1.1％）
ｘ²＋３ｘ－５＝０
解の公式を適用して、
ｘ＝（－３±√29）/２

（６）　18.0％！（部分正答0.1％）
反比例はｘとｙの積が比例定数ａで一定。
ｙ＝16/ｘ
ｘｙ＝16
（ｘ、ｙ）＝（－16、－１）（－８、－２）（－４、－４）（－２、－８）（－１、－16）
（１、16）（２、８）（４、４）（８、２）（16、１）
10個

（７）　41.3％（部分正答0.1％）
底面は正方形→対角線×対角線÷２
４×４÷２×６÷３
＝16ｃｍ³

（８）　64.6％（部分正答0.1％）
四分位範囲＝第３四分位数－第１四分位数
箱の長さが最も長いウ。

大問２（小問集合２）

（１）　46.9％（部分正答2.1％）
ｙ＝ａｘ²に（ｘ、ｙ）＝（３、５）を代入。
５＝９ａ
ａ＝５/９

ｙ＝５/９ｘ²において、
ｘ＝０のとき、最小値ｙ＝０
ｘ＝－６のとき、最大値ｙ＝20
０≦ｙ≦20

（２）　35.5％（部分正答1.5％）

60～120の相対度数は、11/50＝22/100＝0.22
累積相対度数は、その階級以下の相対度数の合計。
累積相対度数の差をとると、相対度数が最が大きいのは120～180の階級。
→度数が最も多い階級は120分以上180分未満。
その階級値は120と180の平均で150分。

（３）　35.8％（部分正答15.0％）
説明問題。
９の倍数を証明したいので、最終的に９でくくる形にもっていく。

もとの数は10ａ＋ｂ。
十の位と一の位を入れ替えた数は10ｂ＋ａ。
４（10ａ＋ｂ）＋５（10ｂ＋ａ）
＝45ａ＋54ｂ
＝９（５ａ＋６ｂ）
５ａ＋６ｂは整数だから、９（５ａ＋６ｂ）は９の倍数。
よって、もとの自然数を４倍した数と、入れ替えた自然数を５倍した数の和は９の倍数。

大問３（平面図形）

（１）　50.1％（部分正答0.1％）

ＡＤ//ＢＣの錯角と仮定で、∠ＢＡＧ＝70°
△ＡＢＧの内角から、∠ＡＢＧ＝180－70×２＝40°
平行四辺形ＡＢＣＤの対角は等しい。∠ＡＤＣ＝40°

（２）　10.3％！（部分正答0.4％）

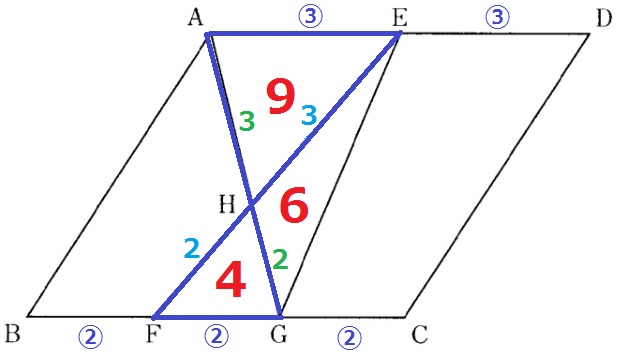
ＡＤを２等分、ＢＣを３等分するので、
ＡＤ、ＢＣの長さを最小公倍数⑥とすると、ＡＥ＝③、ＦＧ＝②
△ＡＥＨ∽△ＧＦＨの相似比は３：２。
ＡＨ：ＨＧ＝３：２より、△ＥＨＧ＝９×２/３＝６
ＥＨ：ＨＦ＝３：２より、△ＥＦＧ＝６×５/３＝10

大問４（関数）

（１）　44.0％（部分正答1.2％）
ＡＣがｘ軸と平行→Ｃのｙ座標はＡと同じ８。
ｙ＝２/３ｘ＋２にｙ＝８を代入する。
８＝２/３ｘ＋２
ｘ＝９

（２）　6.3％!!（部分正答0.4％）

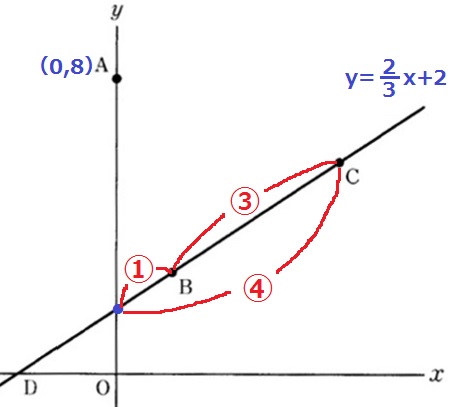
Ｂのｘ座標の４倍がＣのｘ座標。
上図の線分の比が①：③になる。

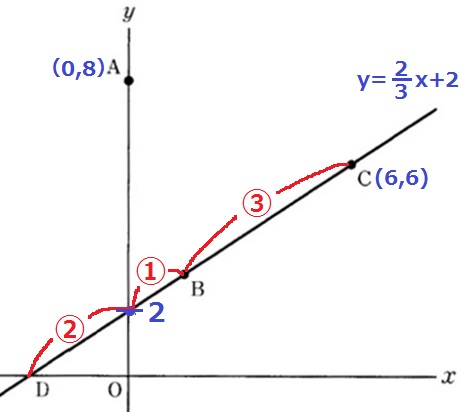
ＤＢ＝ＢＣ＝③、Ｄから切片までは③－①＝②
Ｄから②進むと切片のｙ座標２。
Ｄから⑥進むとＣのｙ座標６。
ｙ＝２/３ｘ＋２にｙ＝６を代入して、Ｃ（６、６）

Ａ（０、８）→Ｃ（６、６）
右に６、下に２なので、傾きは－２/６＝－１/３

大問５（方程式）

（１）　69.4％（部分正答1.5％）
難しくない。
選ばれるのは５人中２人だから２/５。
Ｑが選ばれるのもＳが選ばれるのもみな同様に確率は２/５である。

（２）　11.3％！（部分正答26.3％）
答案では求める過程も記述する。
在校生インタビューと部活動紹介の配分時間の合計は、
15分－（30秒＋６分＋３分＋30秒）＝５分＝300秒
（*公式答案によると、この過程は省いてもＯＫ）

１人あたりの在校生インタビューをｘ秒とする。
１つの部活動紹介に割り当てる時間は1.5ｘ秒なので、
３ｘ+（３×1.5ｘ＋30）＝300
7.5ｘ＝270
ｘ＝36
在校生インタビューの配分時間は、３ｘ＝108秒＝１分48秒
部活動紹介の配分時間は、300－108＝192秒＝３分12秒
ア…１分48秒、イ…３分12秒

大問６（平面図形２）

（１）　28.1％（部分正答36.0％）
△ＣＥＤ≡△ＣＧＢの証明。

正方形ＡＢＣＤの１辺から、ＣＤ＝ＣＢ
正方形ＣＥＦＧの１辺から、ＣＥ＝ＣＧ
∠ＤＣＢ＝∠ＥＣＧ＝∠90°から、あいだの∠ＤＣＧを引くと∠ＤＣＥ＝∠ＢＣＧ
２辺とあいだの角が等しいので合同。

（２）　7.2％!!（部分正答1.1％）

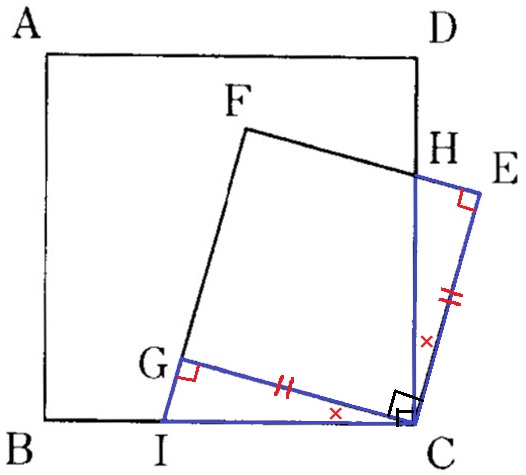
△ＣＥＨ≡△ＣＧＩの理由を一応確認しておくと、
ＣＥ＝ＣＧ（正方形１辺）、∠ＨＥＣ＝∠ＩＧＣ＝90°、
∠ＨＣＥ＝∠ＩＣＧ（90－あいだの∠ＨＣＧ）より、１辺と両端角が等しいから合同。

ア：四角形ＡＩＣＨは菱形である。

菱形は４辺が等しい四角形。隣り合うＡＩ＝ＩＣがいえるか。
ＢＩ＝■、ＩＣ＝〇とする。
正方形の１辺から、ＡＢ＝■＋〇。
ＡＩは直角三角形ＡＢＩの斜辺なので、■＋〇よりも長い。
ＡＩ＞ＩＣから、四角形ＡＩＣＨは菱形ではない。×

イ：四角形ＡＩＣＨの面積は、△ＣＤＩの面積の２倍である。

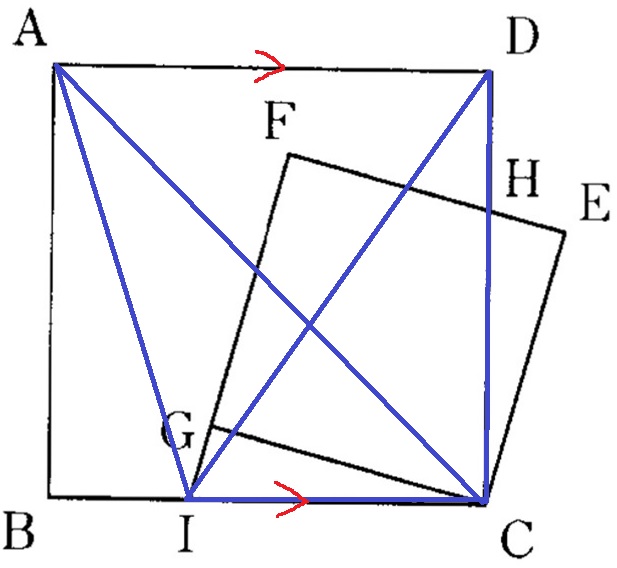
ＡＤ//ＢＣより、等積変形で△ＣＤＩ＝△ＣＡＩ

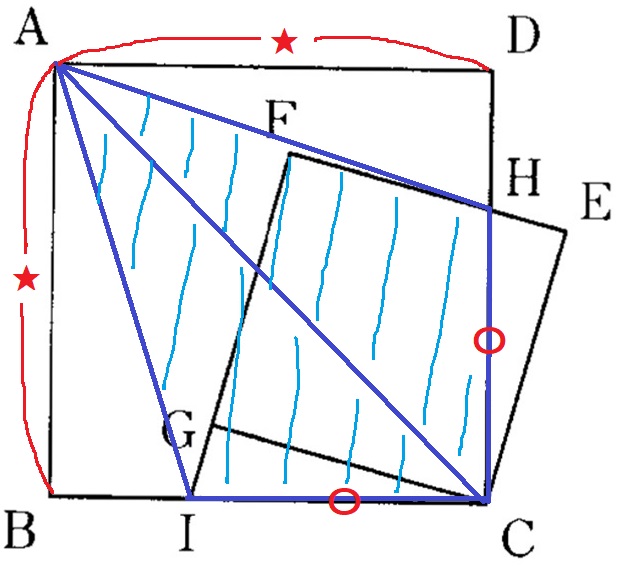
△ＣＡＩの底辺はＩＣ＝〇、高さはＡＢ＝★
△ＣＡＨも底辺はＨＣ＝〇、高さはＡＤ＝★で等積。
四角形ＡＩＣＨの面積は、△ＣＤＩの面積の２倍といえる。〇

ウ：線分ＢＤと線分ＩＨは平行である。

ＢＣ：ＩＣ＝ＤＣ：ＨＣと直角から２辺の比とあいだの角が等しく、△ＢＣＤ∽△ＩＣＨ。
対応する角から同位角が等しく、ＢＤ//ＩＨがいえる。〇

エ：△ＢＩＨ≡△ＤＨＧである。

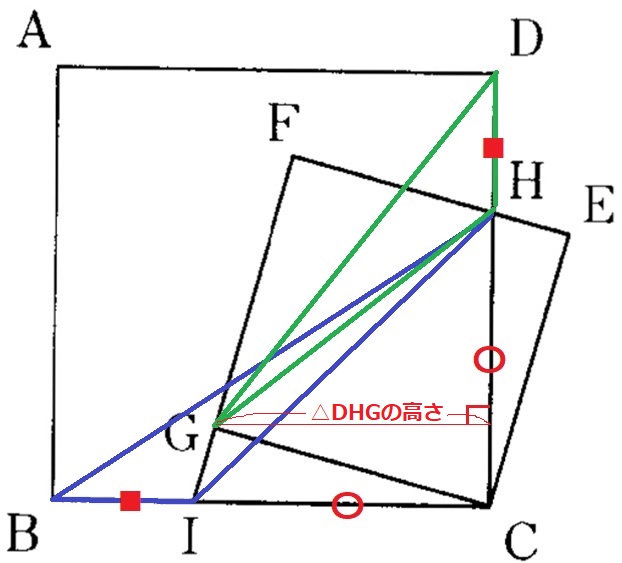
△ＢＩＨの底辺ＢＩ＝■、高さＨＣ＝〇
△ＤＨＧの底辺ＤＨ＝■だが、高さはＩＣ＝〇より短い。
△ＤＨＧの方が面積が小さく、合同とはいえない。×

オ：４点Ｃ、Ｈ、Ｆ、Ｉは１つの円周上にある。

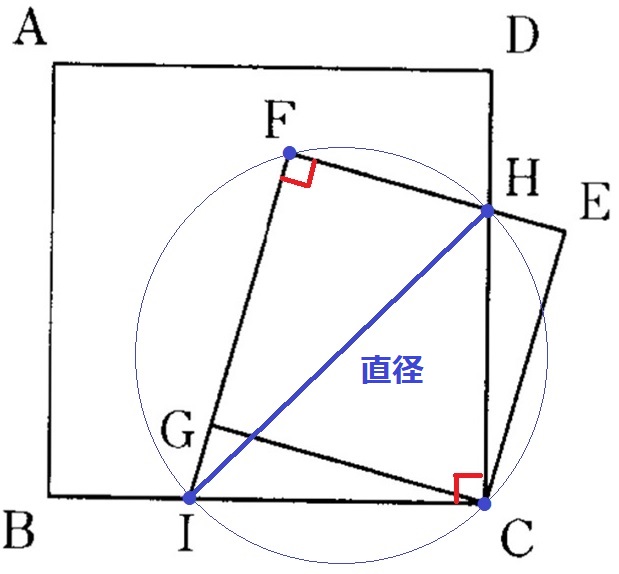
直径に対する円周角は90°。
∠ＨＦＩ＝∠ＨＣＩより、直径をＨＩとする円の円周上に４点Ｃ、Ｈ、Ｆ、Ｉがある。〇
答えはイ・ウ・オ。