2021年度　島根県公立高校入試問題過去問【数学】解説

平均24.9点（前年比；＋0.8点）

問題はコチラ→ＰＤＦファイル
出題範囲の削減はなし。

大問１（小問集合）

（１）
４－12÷２
＝４－６＝－２

（２）
ｘ²＋８ｘ＋12
＝（ｘ＋６）（ｘ＋２）＝０
ｘ＝－６、－２

（３）
連立方程式。
３ｘ－２ｙ＝０　…①
２ｘ＋ｙ＝７　…②
①＋②×２が多いかな？
これを解いてｘ＝２、ｙ＝３

（４）
100ｇあたりａ円⇒300ｇでは３ａ円
100ｇあたりｂ円⇒500ｇでは５ｂ円
３ａ＋５ｂ＝1685

（５）
√８－２/√２
＝２√２－√２
＝√２

（６）
絶対値とは、数直線上で原点０からの距離。
すべて正の数に変え、最も大きな数を選べばいい。
√３＝1.7320508…（人並みにおごれや）
７/３＝2.33…
０＜√３＜２＜７/３
したがって、ウ。

（７）
反比例はｘとｙの積が比例定数ａで一定。
ａ＝－４×２＝－８
ｙ＝－８/ｘ

（８）

△ＥＡＦは二等辺三角形。∠ＥＡＦ＝（180－30）÷２＝75°
平行四辺形に対角は等しいから、∠ＢＡＤ＝130°
ｘ＝130－75＝55°

（９）

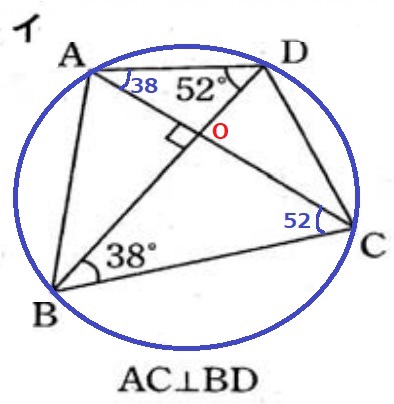
ＡＣとＢＤの交点をＯとする。
外角定理より、∠ＢＣＯ＝90－38＝52°

ここで、円周角の定理の逆を用いる。
『２点Ｃ、Ｄが直線ＡＢについて同じ側にあって、∠ＡＣＢ＝∠ＡＤＢだから、
４点Ａ、Ｂ、Ｃ、Ｄは同一円周上にある』
（∠ＣＡＤ＝∠ＣＢＤを指摘してもよい）
イ

（10）
取り出し方は、３×３＝９通り
50点以下となる組み合わせは、
（０、０）（０、50）（50、０）の３通り。
確率は３/９＝１/３

大問２（データの活用＆整数）

（１）①【１】
昇順に並べると〔１・１・１・２・３・４・４・６・８・10〕。
10個の中央値（メジアン）は５番目と６番目の平均だから3.5点。

【２】
（１＋１＋１＋２＋３＋４＋４＋６＋８＋10）÷10
＝40÷10＝4.0点

②
ａ以外の８個において、平均5.0点との差の合計は、
－４＋（－２）＋５＋（－３）＋１＋０＋（－３）＋（－２）＝－８
２個のａで〔平均＋８〕にすれば、10個の平均が5.0点⇒１個のａは〔平均＋４〕。
ａ＝５＋４＝９

③
１班の中央値3.5点を大きくする。
⇒３点以下の誰かを４点以上の誰かにチェンジ。

平均値は１班10人が4.0点、２班10人が5.0点。
１組の合計…10×4.0＝40点
２組の合計…10×5.0＝50点
１組と２組の平均が等しい⇒１&２組20人全体の平均は、90÷20＝4.5点
（*１組と２組は各10人で同じだから、そのまま4.0と5.0の平均をとっても良い）

１組の平均値を＋0.5点にするので、１組の合計は（＋0.5）×10＝＋５点。
⇒交換する生徒の点数差は５点である。

中央値の条件から交換すべき１班の生徒は１点・２点・３点のいずれか。
１点→６点
２点→７点
３点→８点
２班には７点と８点がいない。
ということは、１班の１点、２班の６点をチェンジした。
ｘ＝１、ｙ＝６

（２）①
３ずつ増えていくので、ア…ｎ＋３　イ…ｎ＋12

ウ…
ｎ＋（ｎ＋３）＋（ｎ＋６）＋（ｎ＋９）＋（ｎ＋12）
＝５ｎ＋30＝５（ｎ＋６）
３列目の数ｎ＋６の５倍である。

②
まず、20行目１列目の数を調べる。
１列目【１、16、31、45…】
初項１、公差15の等差数列。
20行目１列目は、１＋15×（20－１）＝286
前問の式に代入。
５×（286＋６）＝1460

大問３（数量変化）

（１）
「基本支給額」が切片、「部員数によって決まる支給額」が傾き。
図１より、切片は2000。
傾きは（3000－2000）÷10＝100
ア…2000、イ…100

（２）
Ａ中の一次関数の式は、ｙ＝100ｘ＋2000
ｘ＝50を代入。
100×50＋2000＝7000円

（３）①②
先に②のグラフから。

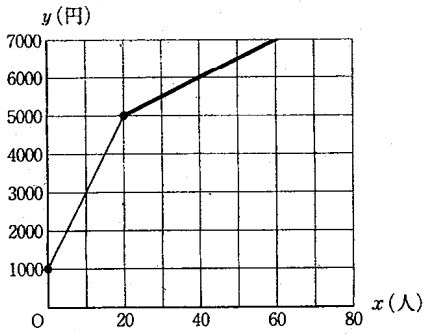
ｘ≧20のとき、傾きは50。
⇒10人で500円増加、20人で1000円増加。
（20、5000）から右２マス、上１マスの傾きで直線をひく。

切片はこの直線をｙ軸方向へ延長すると（０、4000）に交わる。
①ｙ＝50ｘ＋4000

（４）①

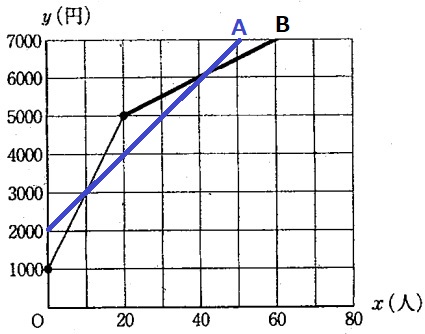
先ほどのグラフにＡを記入。
活動費が等しい⇒ｙの値が等しい、部員数が等しい⇒ｘの値が等しい
グラフの交点のｘ座標が答え。
10人と40人

②

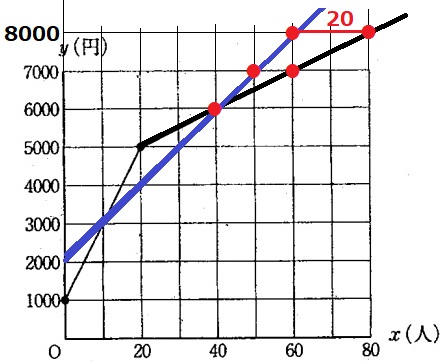
ｙ座標が同じとき、ｘ座標の差が20になるところを探す。
上に延長すると、差が横２マス分はｙ＝8000のとき。
8000円

大問４（関数）

（１）①
ｘ＝０のとき、最小値ｙ＝０
ｘ＝４のとき、最大値ｙ＝８
０≦ｙ≦８

②
ＡＢの傾きを調べる。
Ａ（－２、２）⇒Ｂ（４、８）
右に６、上に６だから傾きは１。
切片にあたるＣのｙ座標はＡから右に２上に２だから、２＋２＝４

③

△ＯＡＢを等積変形。
６×４÷２＝12

（２）①

等積変形。ＡＯ//ＢＰで△ＯＡＢと△ＯＡＰが等積となる。
すなわち、Ｂを通るＡＯに平行な線をひき、ｍとの交点がＰ。
ＡＯの傾きが－１なので、うえのような直角二等辺三角形の相似を描くと見えやすい。
右の大きい直角二等辺の等辺は、ＡとＢのｙ座標の差で６。
Ｐのｘ座標は、４＋６＝10
ｍはｙ＝２の直線だから、Ｐのｙ座標は２。
Ｐ（10、２）

②

四角形ＯＡＢＰは台形。
上底と下底の比の大きさが等しくなれば、台形は二等分される。
先ほどの直角二等辺の相似を手がかりに、ＡＯ＝②、ＢＰ＝⑥とする。
上底と下底の和が⑧だから、④ずつに分ければいい。

△ＡＢＱはＢＱ＝④
四角形ＯＡＱＰは上底②＋下底②＝④（平行四辺形である）

ＢＱ：ＱＰ＝④：②＝２：１
最後にＢＰを２：１に内分するＱの座標を求める。
Ｑ（８、４）

大問５（平面図形）

（１）
三平方の定理。
公式が与えられているのは、コロナによる授業の遅れに配慮したからか。
ｃ²＝３²＋１²＝10
ｃ＞０で、ｃ＝√10

（２）
三平方の定理が成り立つものを探す。
３²＋４²＝５²
イ
*３：４：５で普通に選べる。

（３）

Ｆを通るＤＥにひいた垂線。基本。

（４）①
△ＡＣＨ∽△ＣＢＨの証明。頻出である。

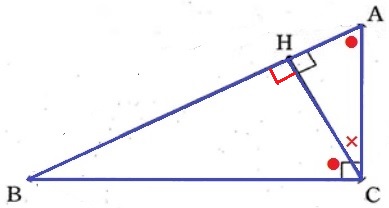
∠ＡＨＣ＝∠ＣＨＢ＝90°
△ＡＣＨの内角で、∠ＣＡＨ（●）＋∠ＡＣＨ（×）＝180－90＝90°
∠ＢＣＨ＝90－×＝●
２角が等しく∽。

②
誘導に従う。

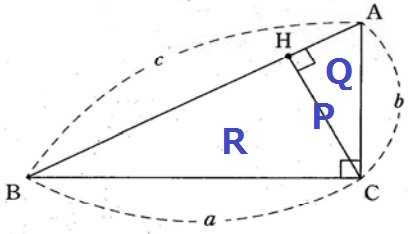
Ｑ（△ＡＣＨ）＋Ｒ（△ＣＢＨ）＝Ｐ（△ＡＢＣ）　…（Ⅰ）

Ｐ：Ｑの相似比はＡＢ：ＡＣ＝ｃ：ｂ。
面積比は相似比の２乗だから、Ｐ：Ｑ＝ｃ²：ｂ²
比例式。内項と外項の積から、Ｑ×ｃ²＝Ｐ×ｂ²
Ｑ＝ｂ²/ｃ²×Ｐ　…（Ⅱ）

ＰとＲも同様。
相似比はＰ：Ｒ＝ＡＢ：ＣＢ＝ｃ：ａ
面積比はＰ：Ｒ＝ｃ²：ａ²
内項と外項の積から、Ｒ×ｃ²＝Ｐ×ａ²
Ｒ＝ａ²/ｃ²×Ｐ　…（Ⅲ）
ア…ｃ²、イ…ｂ²、ウ…ｂ²/ｃ²、エ…ｃ、オ…ａ、カ…ａ²/ｃ²

＠＠
解答はこれで終わりだが、続きを検証する。
Ｑ＋Ｒ＝Ｐ　…（Ⅰ）
Ｑ＝ｂ²/ｃ²×Ｐ　…（Ⅱ）
Ｒ＝ａ²/ｃ²×Ｐ　…（Ⅲ）

Ⅱ、ⅢをⅠに代入。

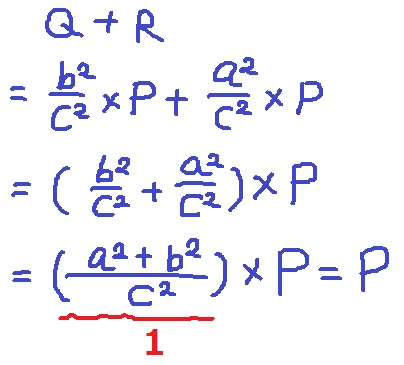
途中で分配法則を適用。
１×Ｐ＝Ｐで等式が成り立つから、赤線のカッコ内が１。

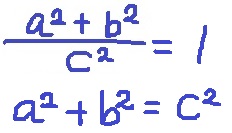
両辺にｃ²をかけるとａ²＋ｂ²＝ｃ²となり、三平方の定理が導けた。