2020年度　山口県公立高校入試問題過去問【数学】解説

平均21.3点（50点満点、前年比；－5.5点）
学校指定教科検査5.0点（15点満点、前年比；±０）
問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）
３＋（－５）
＝３－５＝－２

（２）
６²÷８
＝36/８＝９/２

（３）
－２ａ＋７－（１－５ａ）
＝－２ａ＋７－１＋５ａ
＝３ａ＋６

（４）
（９ａ－ｂ）×（－４ａ）
＝－36ａ²＋４ａｂ

（５）
ｘ³＋２ｘｙ
＝（－１）³＋２×（－１）×７/２
＝－１－７＝－８

大問２（小問集合）

（１）
ｙ＝ａｘにｘ＝６、ｙ＝－９を代入。
－９＝６ａ
ａ＝－３/２
ｙ＝－３/２ｘ

（２）
√45＝３√５
ｎ＝５をいれると３√５×√５＝15でルートが外れる。
ｎ＝５

（３）

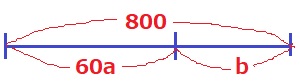
全体が800ｍで、歩いた距離は60ａｍ。
ｂ＝800－60ａ

（４）
回転体は底面の半径が３ｃｍ、高さ８ｃｍの円柱。
３×３×π×８＝72πｃｍ³

大問３（データの活用）

（１）
ア：階級の幅は20。範囲（レンジ；最大値－最小値）が120。×
イ：最頻値（モード）は最もあらわれている値。階級値でいえば30。×
ウ：（８＋４＋０＋２）÷30＝14/30。15/30未満だから半数以下。〇
エ：度数が２人以下の階級は、80～100と100～120の２つ。×
ウ

（２）
各階級値×度数の合計を30人で割る。
（10×６＋30×10＋50×８＋70×４＋90×０＋110×２）÷30
＝1260÷30＝42分

大問４（関数）

（１）
ｙ＝１/４ｘ²にｙ＝５を代入。
５＝１/４ｘ²
ｘ²＝20
ｘ＝±２√５
（２√５、５）、（－２√５、５）

（２）

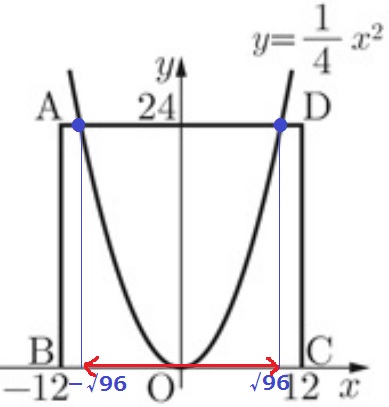
グラフとＡＤの交点の座標を求める。
ｙ＝１/４ｘ²にｙ＝24を代入。
24＝１/４ｘ²
ｘ＝±√96

√81＜√96＜√100だから、９＜√96＜10
－√96≦ｘ≦√96の変域のなかで、自然数は－９～９の範囲。
このなかでｙ＝１/４ｘ²のｙが整数となるのは、
ｘ＝０、±２、±４、±６、±８
よって、９個。

大問５（方程式・確率）

（１）
ａ＝２、ｂ＝５を代入して展開する。
（ｘ＋２）（ｘ＋５）
＝ｘ²＋７ｘ＋10
ｍ＝７、ｎ＝10

（２）
答案では求めるまでの過程も記述する。
出目は全部で、６×６＝36通り

ｘ²＋ｍｘ＋ｎ＝（ｘ＋ａ）（ｘ＋ｂ）or（ｘ＋ｃ）²
サボはｎでまとめてみました。
◆ｎ＝１
積が１→１×１＝１
和は１＋１＝２しかない。ｍ＝２
◆ｎ＝２
積は１×２＝２、和は１＋２＝３。ｍ＝３
◆ｎ＝３
１×３＝３、ｍ＝１＋３＝４
◆ｎ＝４
２×２＝４→ｍ＝２＋２＝４
１×４＝４→ｍ＝１＋４＝５
◆ｎ＝５
１×５→ｍ＝１＋５＝６
◆ｎ＝６
１×６＝６だが、１＋６＝７は６を超えるので×！
２×３＝６、ｍ＝２＋３＝５
計７通り。
確率は７/36

大問６（作図）

25°の作成。
変則的な作図問題で応用力が試される。

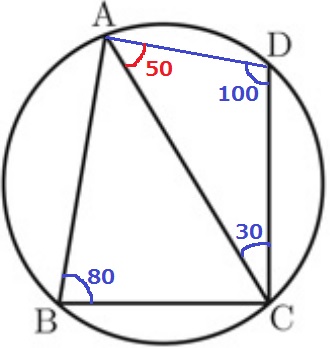
ひとまず、角度の調査をする。
ＡＤに補助線。四角形ＡＢＣＤは円に内接する四角形。
内接四角形の対角の和は180°だから、∠ＡＤＣ＝180－80＝100°
∠ＤＡＣ＝180－（100＋30）＝50°
50°の半分が25°！

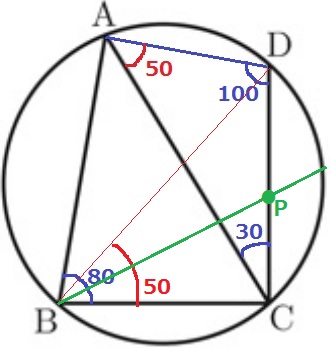
円周角定理で、∠ＤＢＣ＝50°
∠ＤＢＣの二等分線を描き、線分ＣＤとの交点がＰとなる。

大問７（規則・整数）

（１）

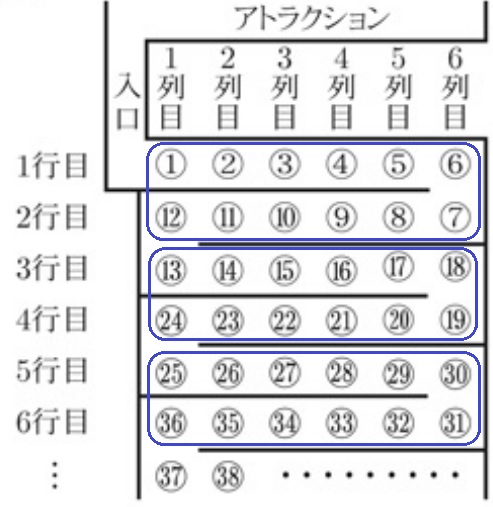
２行ずつ、12個単位で見ていく。
75÷12＝６…３
６つのカタマリ＋３だから、２×６＝12行と３列目。
13行目の３列目

＠別解＠
１行６個単位でもいい。
奇数行目は左→右、偶数行目は右→左に変わることに注意する。
75÷６＝12…３
13行目は左→右だから、13行目の３列目。

（２）

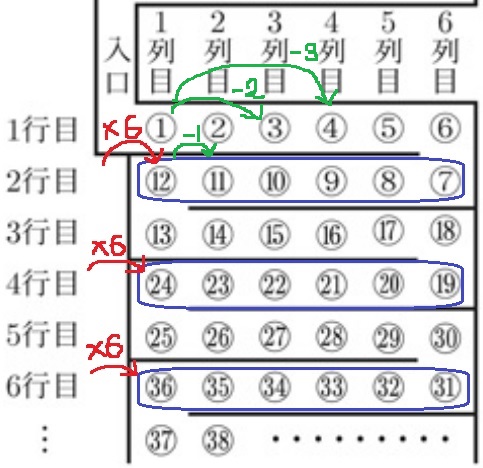
偶数行目と１列目の番号の関連性を調べると、
〇行目の６倍の値が１列目の番号。
２ｍ行目の１列目は、２ｍ×６＝12ｍ

２列目の数は１列目の－１、３列目は－２、４列目は－３…
ということは、１列目の数からｎ－１を引く。
よって、12ｍ－（ｎ－１）＝12ｍ－ｎ＋１

＠＠
後半は、偶数行目の５列目が４の倍数であることを証明する。
ｎ＝５なので、12ｍ－５＋１＝12ｍ－４＝４（３ｍ－１）
３ｍ－１は整数だから、４（３ｍ－１）は４の倍数であり、
Ｂさんの整理券の番号は４の倍数である。

大問８（平面図形）

（１）

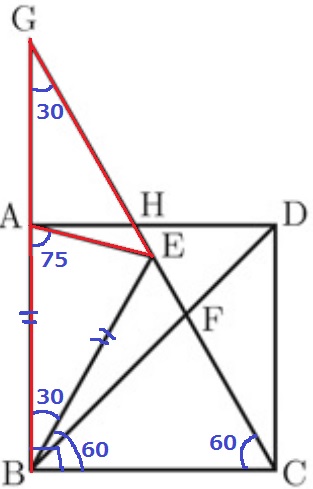
↑問題文の角度を示すとこのような感じ。
最後に△ＡＥＧで外角定理を用いる。
外角定理…三角形の外角は、それと隣り合わない２つの内角の和に等しい。
エ

（２）
△ＡＥＧ≡△ＦＤＣの証明。

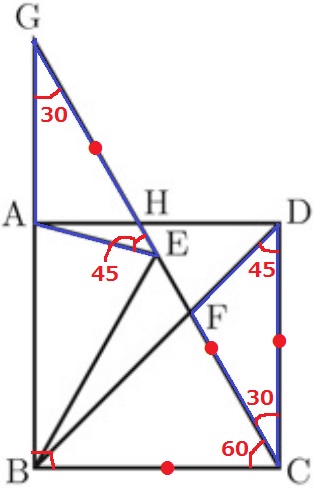
先ほどのＡＥＧ＝∠45°と、正方形の対角線から∠ＦＤＣ＝45°
ＧＢ//ＤＣ→錯角で∠ＡＧＨ＝∠ＦＣＤ（＝30°）

２角がわかったので、辺の情報が欲しい。
ＣＤは正方形の１辺●。ＣＢとＣＥも正三角形の１辺で●。
△ＢＣＧの内角は30°－60°－90°であるから、辺の比は１：２：√３。
ということは、ＧＣ＝●●となり、ＧＥ＝●●－●＝●＝ＣＤ
以上、１辺と両端角が等しいので合同。

（３）
大問が９つもあるので、そんなに時間はかけられない。

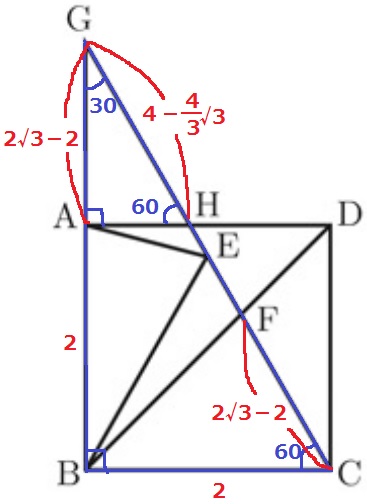
△ＧＢＣ∽△ＧＡＨ。
１：２：√３より、ＧＢ＝２√３ｃｍ
ＧＡ＝２√３－２ｃｍ
先ほどの合同より、ＣＦ＝ＧＡ＝２√３－２ｃｍ
△ＧＡＨも１：２：√３なので、ＧＨ＝（２√３－２）×２/√３＝４－４√３/３

ＡＣ＝２×２＝４ｃｍだから、
ＦＨ＝４－（４－４√３/３＋２√３－２）
＝２－２√３/３ｃｍ

大問９（総合問題）

（１）ア
携帯をｘ台、ノートパソコンをｙ台として連立を組む。
（金）…0.05ｘ＋0.30ｙ＝190
（銀）…0.26ｘ＋0.84ｙ＝700

100倍して整理。
５ｘ＋30ｙ＝19000　…①
26ｘ＋84ｙ＝70000　…②
①×26－②×５
130ｘ＋780ｙ＝494000
－)130ｘ＋420ｙ＝350000
360ｙ＝144000
ｙ＝400
①に代入。５ｘ＋30×400＝19000
ｘ＝1400
携帯電話…1400台、ノートパソコン…400台

＠都市鉱山＠

エコジンより。仮想の話ではなく環境省が取り組んでいます。
社会科でもレアメタルに関連して都市鉱山を習いますよね。
都市をレアメタルや貴金属の鉱山にみたて、その回収とリサイクルで循環を促す。

イ
推論問題。
ａ以外の金メダルの個数を昇順になおすと、【10・11・12・13・16】
６個の中央値は３番目と４番目の平均。
中央値が12.5ということは12と13の平均なので、ａは13～16の範囲。
同様に、ｂ以外の銅メダルの個数を昇順になおすと、【７・８・12・14・21】
中央値10は８と12の平均なので、ｂは７～８の範囲。

④のメダルの総数は、ａ＋５＋ｂ＝29
ａ＋ｂ＝24

まとめると、
13≦ａ≦16、７≦ｂ≦８、ａ＋ｂ＝24
ａ＝16、ｂ＝８の組み合わせしかない。
ａ…16、ｂ…８

（２）ア

横⑯＝２ｍ
縦⑨＝２×９/16＝９/８ｍ
大型スクリーンは、この長方形と相似で面積が８倍。
面積比は辺の比の２乗→辺の比は面積比の正の平方根。
つまり、辺の長さを√８倍する。
９/８×√８＝９√２/４ｍ

イ
Ｐ社は一律125円だから、30000÷125＝240枚
Ｑ社で最も安いの値段は100円だが、これは301枚からスタートである。
100円×300枚＝３万だから、お金が足りない。×
次点の120円で計算する。
30000÷120＝250枚
Ｑ社、最大250枚

学校指定教科検査問題

（１）ア

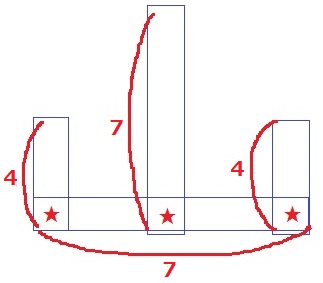
留意点は両サイドに１人ずつ立つので、各辺ごとに辺の長さ＋１。
ａ＝３は４人。２ａ＝６は７人。
また、交差する場所が３つあるので、最後に３をひくこと！
４＋７＋４＋７－３＝19人

イ

ａは先ほどと同じ。
{（ａ＋１）＋（２ａ+１）}×２－３
＝６ａ＋１人
ｂの１辺はｂ＋１人だが、うえのように魔方陣の考えで４ｂ人。

（２）

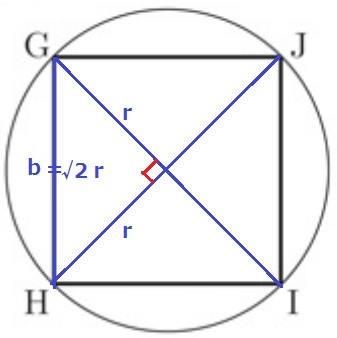
直角二等辺の辺の比は１：１：√２。
ｂ＝√２ｒ
ｒ＝√２/２ｂ

＠＠
後半はグラフの選択。
ｂ＝√２ｒで考えるのがわかりやすい。
ｒの係数に根号がついているが、形はｙ＝ａｘで比例→ウかエ
√２＝1.41421356…（一夜一夜に人見頃）
ｒ＝１のとき、ｂ＝1.41…のグラフはウ。
*ｂが横軸でｒが縦軸である点に注意！

（イ）

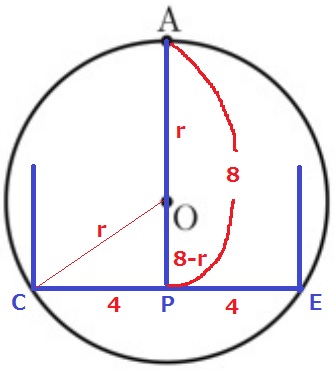
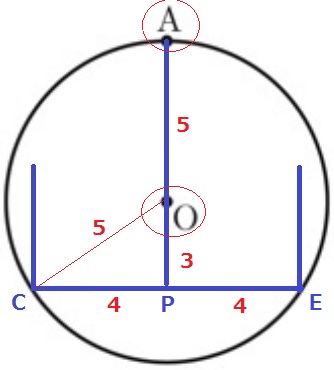
ＣＥの中点をＰとする。ＣＰ＝８÷２＝４ｍ
半径ＯＣが知りたい。これを斜辺とする△ＯＰＣに狙いを定める。
半径ＯＣ＝ＯＡ＝ｒをすると、ＡＰ＝ＣＥ＝８ｍだから、ＯＰ＝８－ｒｍ
△ＯＰＣで三平方。
ｒ²＝（８－ｒ）²＋４²
ｒ²＝64－16ｒ＋ｒ²＋16
ｒ＝５
５ｍ

＠＠
後半はＣの作図。

ＡとＯと円しか与えられてない状態でＣの位置を特定したい。
数値がちりばめられている作図問題では、数字をうまく使う。

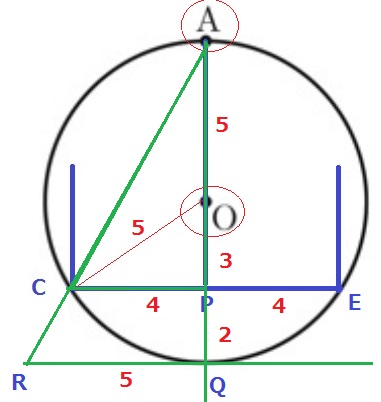
ポイントは、ＡＰ：ＣＰ＝８：４＝２：１。
そして、円外に注意を向けること！
Ａの反対側の円周上の点をＱとすると、直径ＡＱは10ｍ。
△ＡＣＰと相似にある△ＡＲＱをつくれば、斜辺ＡＲと円との交点がＣである。
ＡＱ：ＲＱ＝２：１だから、ＲＱ＝５ｍ。これは円の半径に相当する。

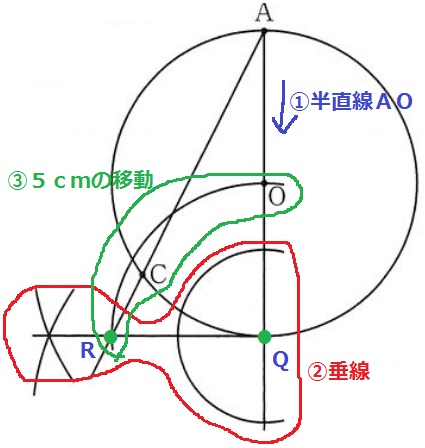
①半直線ＡＯをひく。
②Ｑを通る、半直線ＡＯの垂線。
③ＯＱ＝５ｍを垂線方向に移動。交点がＲ。
あとは、ＡＲを結び、円との交点がＣとなる。