2024年度　三重県公立高校入試問題・後期過去問【数学】解説

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
７×（－６）
＝－42

（２）
３/２ｘ－２/３ｘ
＝５/６ｘ

（３）
（－21ｘ²ｙ）÷３ｘｙ
＝－７ｘ

（４）
４ｘ－５ｙ＝７　…①
２ｘ＋３ｙ＝－２　…②
①－②×２をすると、－11ｙ＝11
ｙ＝－１
②に代入、ｘ＝１/２
ｘ＝１/２、ｙ＝－１

（５）
ｘ²＋５ｘ－36
＝（ｘ＋９）（ｘ－４）

（６）
２ｘ²＋５ｘ－１＝０
解の公式を適用して、ｘ＝（－５±√33）/４

（７）
120を素因数分解すると、120＝２³×３×５
各素因数が偶数個になれば平方数になる。
ｎ＝２×３×５＝30
*120×30＝２⁴×３²×５²＝（２²×３×５）²＝60²

（８）
ｘ＝２のとき、ｙ＝10
ｘ＝４のとき、ｙ＝５
５≦ｙ≦10

（９）

四分位範囲＝第３四分位数（Q3）－第１四分位数（Q1）
＝22－14＝８点

（10）
多角形の外角の和は360°
正十角形の１つの外角は、360÷10＝36°
１つの内角は、180－36＝144°

＠別解＠
ｎ角形の内角の和は180（ｎ－２）
正十角形の内角の和÷10
＝180×（10－２）÷10＝144°

（11）
側面の扇形の中心角は〔×半径/母線〕で出る。
360×５/８＝225°

（12）

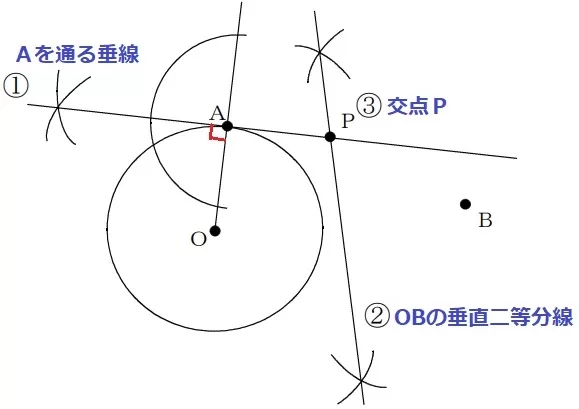
①『点Ａを接点とする接線上にある』
→半径と接線は直交する→半直線ＯＡをひき、Ａを通る垂線をひく。
②『ＯＰ＝ＢＰ』→ＰはＯとＢから等距離にある→ＯＢの垂直二等分線。
③これらの交点がＰ。

大問２（データの活用）

（１）
累積度数…その階級までの度数の和。
３＋４＋３＝10人

（２）

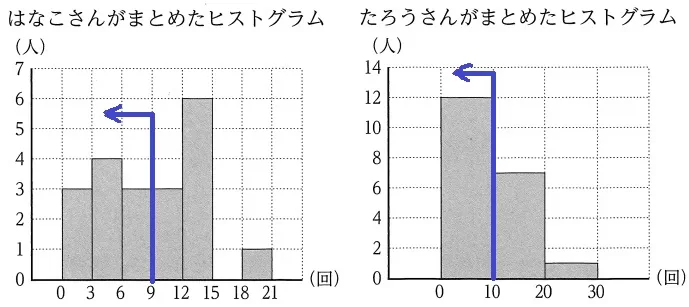
階級の幅が異なる２つのグラフから９回だけを抜き出す。
前問を手がかりにすると見つけやすい。
（０回以上10回未満）－（０回以上９回未満）＝９回
12－10＝２人

大問３（確率）

（１）
玉が少ないよしこが勝つ場合を調べる。
●１→勝てない。
●３→３未満の２
●６→６未満の２・４・５
●８→８未満の２・４・５・７
計８通り。
全体は５×４＝20通りなので、かずきが勝つ場合は20－８＝12通り
確率は12/20＝３/５

（２）
よしこの勝ちが８通り、かずきの勝ちが12通りであった。
それぞれが10通りずつになれば、勝率が等しくなる。

よしこの勝ちを＋２にする→なるべく大きい数をもらう。
９をもらうと＋４になってしまう。×
７をもらうと２・４・５で勝って９で負ける→＋３－１＝＋２
したがって、７。

大問４（方程式）

（１）
〈けいた〉
一次方程式。Ａ組の生徒をｘ人とする。
りんごは３個ずつ配って７個余る→３ｘ＋７個
みかんは５個ずつ配って３個不足→５ｘ－３個
りんごとみかんの合計が140個だから、
（３ｘ＋７）＋（５ｘ－３）＝140

〈のぞみ〉
連立方程式。りんごをｘ個、みかんをｙ個とする。
合計で等式、ｘ＋ｙ＝140
もう１つは生徒の人数で等式を立てる。
配るべきりんごの合計はｘ－７個。
１人に３個ずつ配るので、人数は（ｘ－７）/３人。
配るべきみかんの合計はｙ＋３個。
１人に５個ずる配るので、（ｙ＋３）/５人。
（ｘ－７）/３＝（ｙ＋３）/５
①…３ｘ＋７、②…５ｘ－３、③…（ｘ－７）/３、④…（ｙ＋３）/５

（２）
けいたがわかりやすいかな？
（３ｘ＋７）＋（５ｘ－３）＝140
８ｘ＝136
ｘ＝17（Ａ組の人数）
りんご…３ｘ＋７＝58個
みかん…５ｘ－３＝82個
Ａ組の生徒…17人、りんご…58個、みかん…82個

大問５（関数）

（１）
ｙ＝１/３ｘ²にｘ＝－６を代入する。
ｙ＝１/３×（－６）²＝12
Ａ（－６、12）

（２）

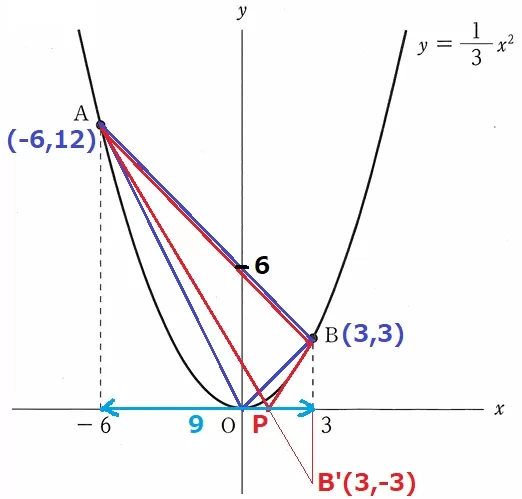
Ａ（－６、12）→Ｂ（３、３）
右に９、下に９だから、傾きは－９/９＝－１
Ｂから左に３、上に３移動して、切片は３＋３＝６
９×６÷２＝27ｃｍ²

（３）
ＡＰ＋ＢＰが最小となる。
ｘ軸についてＢを対称移動させたＢ’（３、－３）とＡを結び、ｘ軸との交点がＰとなる。
（線対称からＰＢ’＝ＰＢ）
ｘ軸上でＰはＯの右側にある→Ｐの方が底辺ＡＢに近い＝高さが短い→△ＯＡＢ＞△ＰＡＢ
イ

（４）

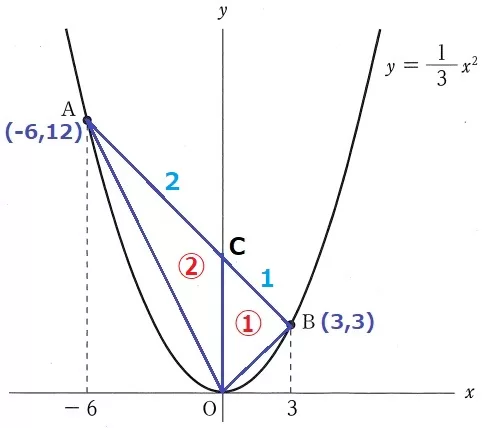
ＡＢの切片をＣとする。
ＣＯで△ＯＡＢを分けると、ＡＣ：ＣＢ＝△ＯＡＣ：△ＯＢＣ＝②：①

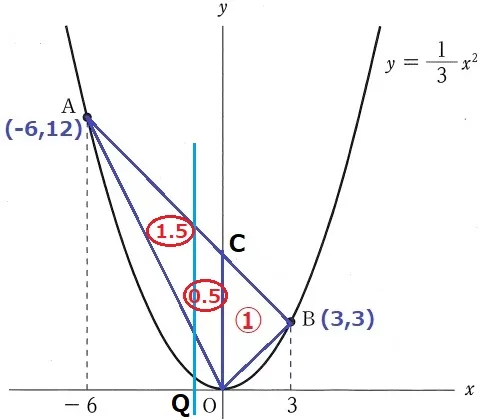
△ＯＡＢ＝③だから、左右で〇1.5ずつに分ければいい。
△ＯＡＣ（②）を〇1.5：〇0.5＝３：１に分ける。

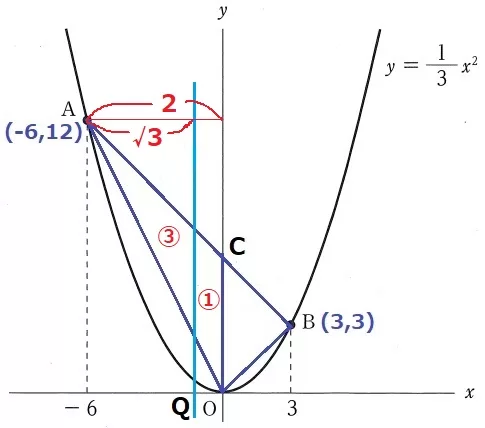
三角形の面積比が３：４→相似比は√３：２
Ａからｙ軸までの距離を２とすると、２等分線までの距離は√３。
２等分線までの距離は、６×√３/２＝３√３
Ａのｘ座標が－６だから、Ｑのｘ座標は－６＋３√３。

大問６（平面図形）

（１）
△ＡＢＦ∽△ＡＤＧの証明。

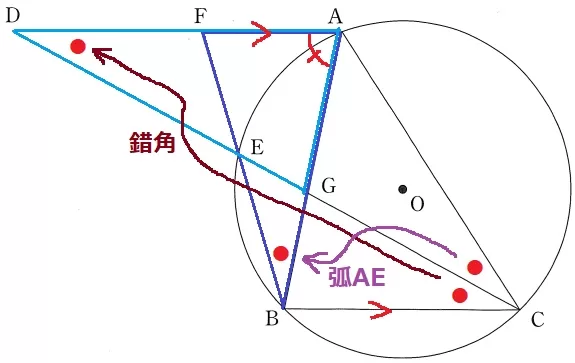
共通角より、∠ＢＡＦ＝∠ＤＡＧ
仮定より、∠ＡＣＥ＝∠ＢＣＥ（●）
これを弧ＡＥに対する円周角とＤＡ//ＢＣの錯角で移動させて、
∠ＡＢＦ＝∠ＡＤＧ
２角が等しいから∽

（２）①

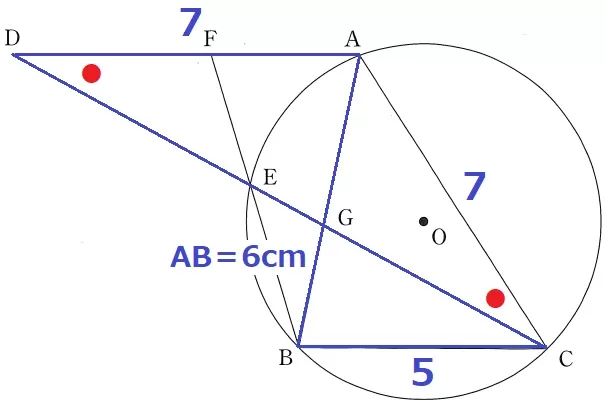
前問の等角に注目すると、△ＡＤＣは２つの底角が等しい二等辺三角形。
ＡＤ＝７ｃｍ
△ＡＤＧ∽△ＢＣＧよりＡＧ：ＧＢ＝⑦：⑤だから、
ＡＧ＝６×⑦/⑫＝７/２ｃｍ

②
ＡＧから新たに長さがわかる線分はどこか。

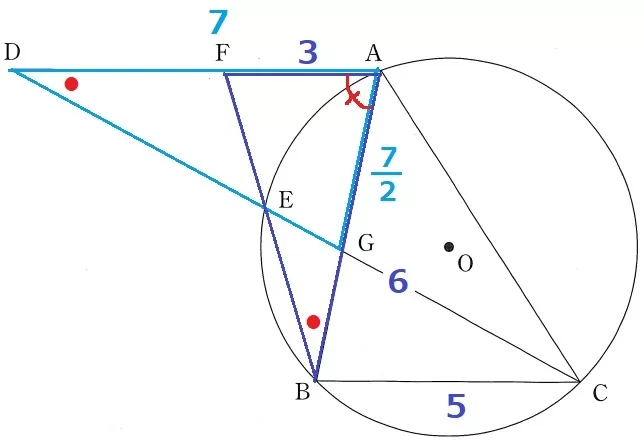
（１）△ＡＢＦ∽△ＡＤＧより、ＡＢ：ＡＦ＝ＡＤ：ＡＧ＝７：７/２＝２：１
ＡＦ＝６÷２＝３ｃｍ

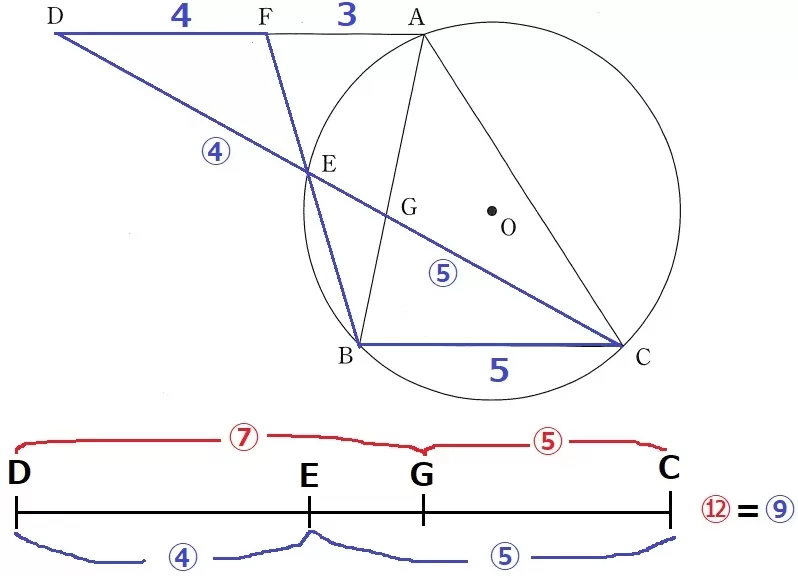
ＤＦ＝７－３＝４ｃｍ
△ＤＥＦ∽△ＣＥＢより、ＤＥ：ＥＣ＝④：⑤
前問より、ＤＧ：ＧＣ＝⑦：⑤
連比。⑫＝⑨だから赤を３倍、青を４倍して比を合成する。

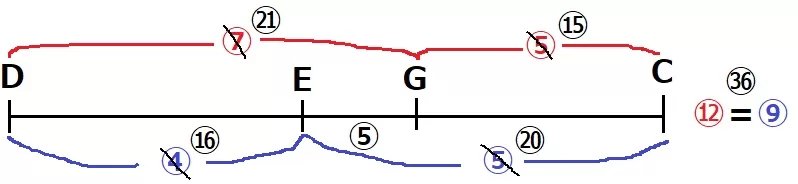
ＤＥ：ＥＧ：ＧＣ＝16：５：15

大問７（空間図形）

（１）
△ＥＡＭは正三角形の半分→辺の比は１：２：√３
ＡＭ＝２ｃｍ、ＥＭ＝２√３ｃｍだから、面積は２×２√３÷２＝２√３ｃｍ²

（２）

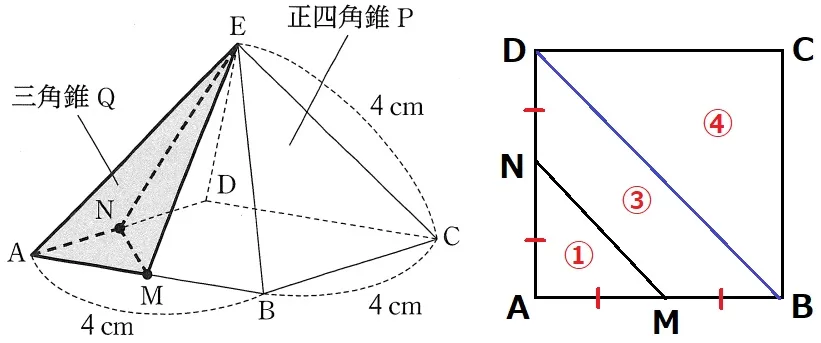
ＰとＱは高さが共通なので、面積比が体積比に値する。
ＭとＮは中点→△ＡＭＮ：△ＡＢＤ＝①：④、△ＣＢＤ＝△ＡＢＤ＝④
体積比は、Ｐ：Ｑ＝正方形ＡＢＣＤ：△ＡＭＮ＝８：１

（３）

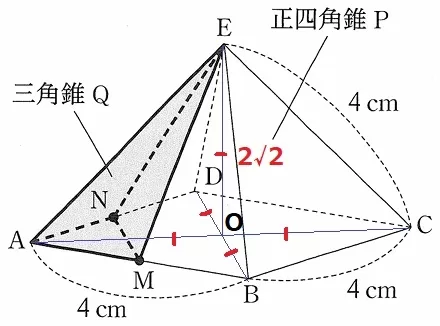
ＡＣとＢＤの交点をＯとする。
△ＡＢＣは直角二等辺→辺の比は１：１：√２だからＡＣ＝４√２ｃｍ
△ＡＢＯと△ＡＥＯは斜辺が４ｃｍである合同の直角二等辺。
→ＥＯ＝ＡＯ＝４√２÷２＝２√２ｃｍ（正四角錘の高さ）

【方針；Ｐの体積→Ｑの体積→底面△ＥＡＭで割って高さを求める】
（２）よりＰ：Ｑ＝８：１だから、Ｑの体積は４×４×２√２÷３÷８＝４√２/３ｃｍ³
（１）より△ＥＡＭ＝２√３ｃｍ²だから、高さは４√２/３×３÷２√３＝２√６/３ｃｍ
公立高校入試解説ページに戻る