2023年度　青山学院高等部過去問【数学】大問７解説

問題ＰＤＦ

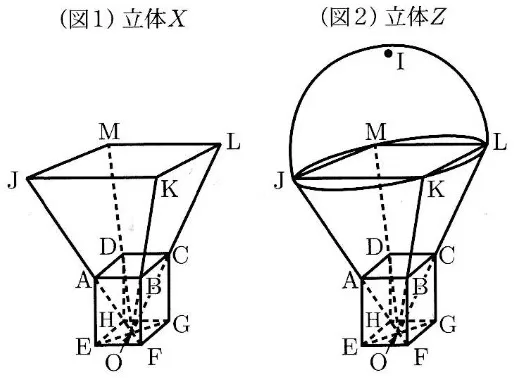
　図１のように、ＡＢ＝ＡＤ＝２ｃｍ、ＡＥ＝２√２ｃｍであるふたのない直方体形の容器ＡＢＣＤ―ＥＦＧＨに正四角すいＯ―ＪＫＬＭを逆さに入れた立体Ｘがある。ただし、直方体の辺ＡＢ、ＢＣ、ＣＤ、ＤＡはそれぞれ正四角すいの側面上にあり、頂点Ｏは底面ＥＦＧＨの対角線の交点と一致している。
　次に、図２のように、正方形ＪＫＬＭのすべての頂点が円周上にあるような円を底面とする半球Ｓを立体Ｘの上にのせ、この立体をＺとする。点Ｏから球面までの距離が最大となる球面上の点をＩとするとき、ＯＩ＝９√２ｃｍであった。

（１）
半球Ｓの半径ｒを求めよ。

（２）
線分ＪＫの長さを求めよ。

（３）
線分ＪＫ、ＬＭの中点をそれぞれＰ、Ｑとするとき、
この立体を３点Ｐ、Ｑ、Ｏを通る平面で切った切り口の形は下図のうちどれか、番号で答えよ。

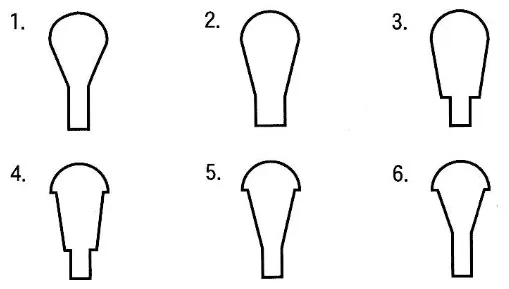
（４）
（３）の切り口の面積を求めよ。

（１）

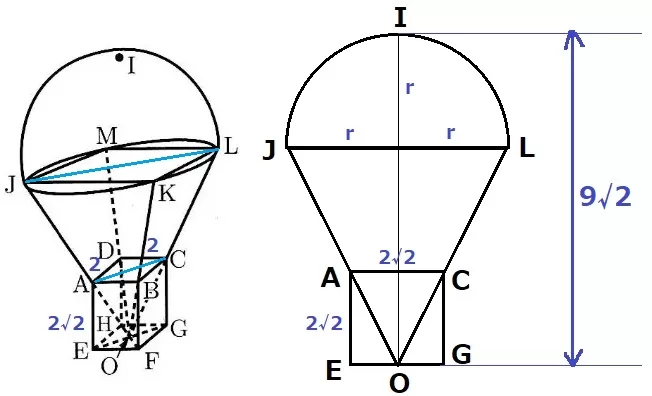
半球の半径ｒを求めたいので、ｒが断面にくる面で切り取る。
△ＡＢＣは直角二等辺→ＡＣ＝２√２ｃｍ

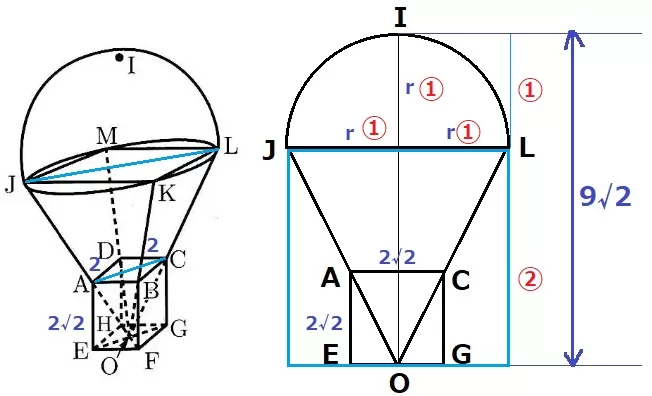
四角形ＡＥＧＣは正方形。１辺をＡＣ→ＪＬに拡大した水色の四角形も正方形。
ｒ＝①とすると、水色の正方形の１辺は②→９√２ｃｍ＝③

（２）
ＪＬ＝３√２×２＝６√２ｃｍ
△ＪＫＬは直角二等辺→ＪＫ＝６√２×１/√２＝６ｃｍ

（３）

問題文はＪＫとＬＭの中点だが、90°回転で一致する立体なので、
ＪＭとＫＬの中点を通る断面図でも同じである。
５

（４）

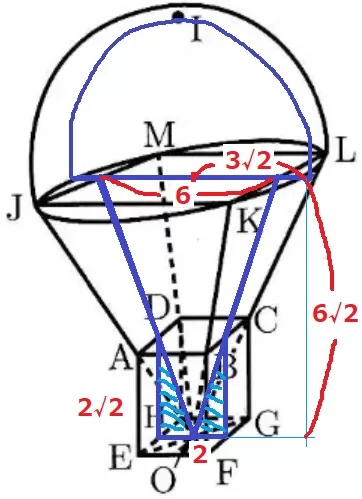
上図のように分割する。
半径３√２ｃｍの半円＋高さ６√２ｃｍの三角形＋斜線２つの三角形は四角形ＡＥＦＢの半分。
３√２×３√２×π÷２＋６×６√２÷２＋２×２√２÷２
＝９π＋20√２ｃｍ²
国私立高校入試解説ページに戻る