2024年度　都立高校入試問題・分割後期過去問【数学】解説

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
９＋６÷（－１/２）
＝９－12
＝－３

（２）
（３ａ－ｂ）/４－（５ａ＋７ｂ）/８
＝｛２（３ａ－ｂ）－（５ａ＋７ｂ）｝/８
＝（６ａ－２ｂ－５ａ－７ｂ）/８
＝（ａ－９ｂ）/８

（３）
（√６－１）²
＝６－２√６＋１
＝７－２√６

（４）
７（ｘ－２）＝５ｘ－４
７ｘ－14＝５ｘ－４
２ｘ＝10
ｘ＝５

（５）
ｙ＝ｘ＋１　…①
ｘ－２ｙ＝－９　…②
①を②に代入、ｘ－２（ｘ＋１）＝－９
ｘ＝７
①に代入、ｙ＝７＋１＝８
ｘ＝７、ｙ＝８

（６）
ｘ²＋３ｘ－８＝０
解の公式を適用して、ｘ＝（－３±√41）/２

（７）
ｙ＝１/２ｘ²は下に凸のグラフ。
原点を通過するので、ｘ＝０のとき、最小値ｙ＝０
ｘ＝６のとき、最大値ｙ＝１/２×６²＝18
０≦ｙ≦18（ウ）

（８）
『ｂがａの約数になる』→ａで場合分け。
ａ＝１→ｂ＝１
ａ＝２→ｂ＝１・２
ａ＝３→ｂ＝１・３
ａ＝４→ｂ＝１・２・４
ａ＝５→ｂ＝１・５
ａ＝６→ｂ＝１・２・３・６
計14通り。全体は６×６＝36通りだから、確率は14/36＝７/18
あ…７、い…１、う…８

（９）

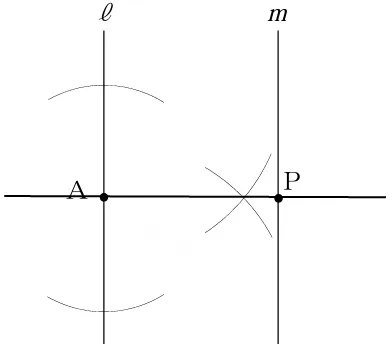
Ａを通る直線ℓに対する垂線をひき、直線ｍとの交点がＰ。

大問２（文字式）

（１）

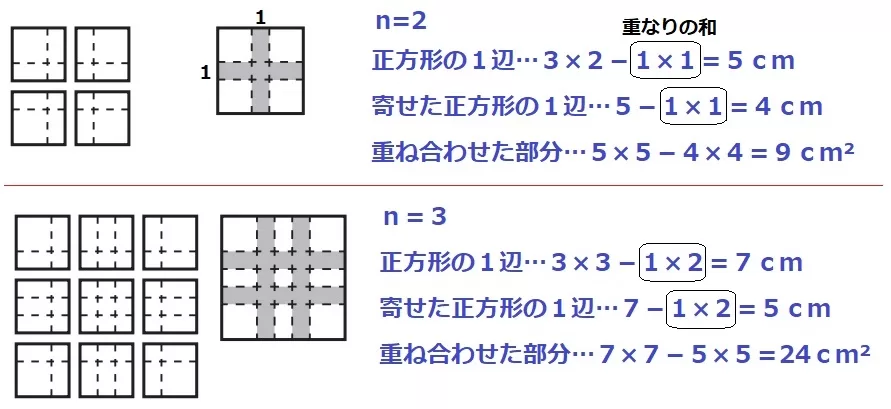
正方形の１辺は、３ｃｍ×枚数分の長さから重なり部分の和（１ｃｍ×間の数）をひく。
白い部分を四隅に寄せた正方形の１辺は、さらに重なり部分の和をひく。
２つの正方形の差が重なり部分の面積になる。

ｎ＝５
正方形の１辺…３×５－１×４＝11ｃｍ
寄せた正方形の１辺…11－１×４＝７ｃｍ
重ね合わせた部分の面積…11×11－７×７＝72ｃｍ²
ウ

（２）
説明問題。
３の倍数であることを証明する→３でくくる形を意識する。

正方形の１辺…３ｎ－１（ｎ－１）＝２ｎ＋１ｃｍ
寄せた正方形の１辺…（２ｎ＋１）－（ｎ－１）＝ｎ＋２ｃｍ
Ｐの面積…（２ｎ＋１）²－（ｎ＋２）²
＝４ｎ²＋４ｎ＋１－ｎ²－４ｎ－４
＝３ｎ²－３
＝３（ｎ²－１）
ｎは２以上の自然数なのでｎ²－１は整数だから、３（ｎ²－１）は３の倍数。
したがって、Ｐは３の倍数になる。

大問３（関数）

（１）
ｙ＝－１/２ｘ＋７にｙ＝10を代入する。
10＝－１/２ｘ＋７
ｘ＝－６
ア

（２）
ｙ＝－１/２ｘ＋７にｘ＝８を代入。
ｙ＝－１/２×８＋７＝３
Ｃ（－４、－３）→Ｐ（８、３）
右に12、上に６だから、傾きは６/12＝１/２
Ｃから右に４、上に２移動して、切片は－３＋２＝－１
ｍ：ｙ＝１/２ｘ－１
①…ウ、②…イ

（３）

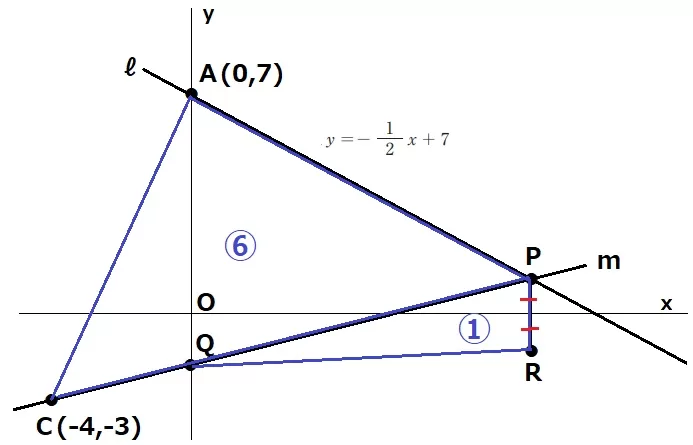
Ｃの位置は変わらない。ℓとｍの交点であるＰの位置が変わる。
△ＡＣＰ：△ＰＲＱ＝⑥：①

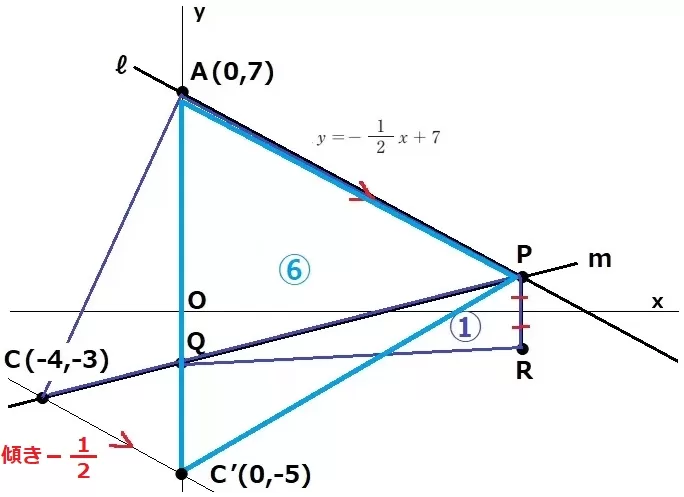
Ｃを通るℓに平行な線をひき、ｙ軸との交点をＣ’とする。
傾きは－１/２だから、Ｃから右に４、下に２移動して、Ｃ’（０、－５）
等積変形で△ＡＣ’Ｐ＝⑥、ＡＣ’//ＰＲ
△ＡＣ’Ｐと△ＰＱＲは高さ一定なので、底辺の比が面積比あたる。
すなわち、ＡＣ’：ＰＲ＝６：１

ＡＣ’＝７－（－５）＝12
ＰＲ＝12×１/６＝２
ＲはＰとｘ軸について対称だから、Ｐのｙ座標は１。
これをｙ＝－１/２ｘ＋７に代入すると、ｘ＝12

大問４（平面図形）

（１）

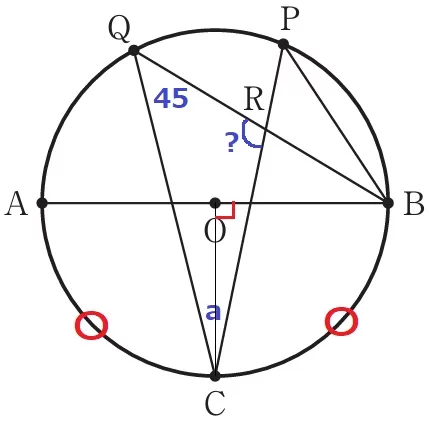
直径ＡＢ→弧ＡＢは半円の弧。
弧ＡＣ＝弧ＢＣということは、弧ＢＣは４分の１円の弧である。
∠ＢＯＣ＝90°、その円周角である∠ＢＱＣ＝45°
△ＣＲＱの内角から、∠ＣＲＱ＝180－（45＋ａ）＝135－ａ°
イ

（２）①
△ＢＳＱが二等辺三角形である証明。
平行と円しかないので、角度（２つの底角）を狙う。

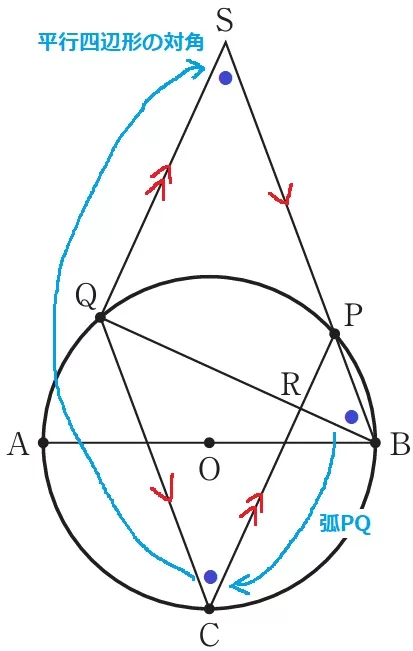
弧ＰＱの円周角で∠ＰＢＱ＝∠ＰＣＱ
ＰＳ//ＣＱとＣＰ//ＱＳから四角形ＣＰＳＱは２組の対辺が平行→平行四辺形。
対角は等しいので、∠ＰＣＱ＝∠ＰＳＱ
∠ＢＳＱ＝∠ＳＢＱで２つの底角が等しいから、△ＢＳＱは二等辺三角形。

②

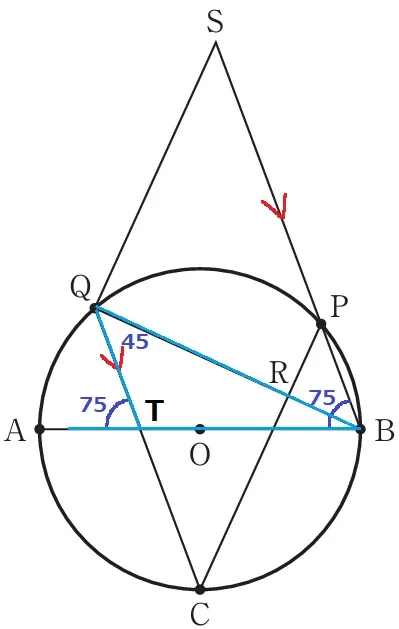
ＡＢとＣＱの交点をＴとする。
ＢＰ//ＣＱの同位角で、∠ＡＴＱ＝75°
（１）より、∠ＢＱＣ＝45°であった。
△ＱＢＴで外角定理→∠ＱＢＴ＝75－45＝30°

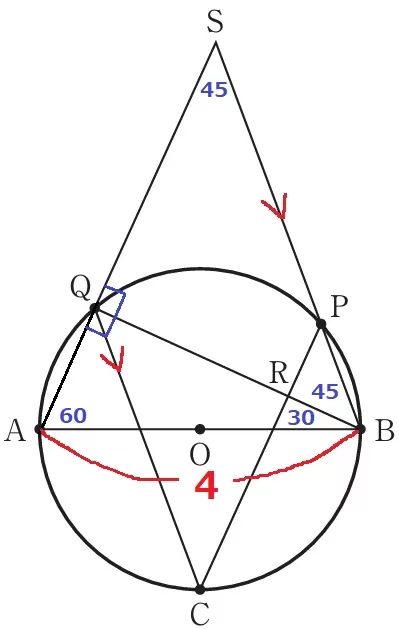
∠ＳＢＱ＝75－30＝45°
（２）①から△ＢＳＱは二等辺→内角は45°―45°―90°だから直角二等辺。
ＡＱに補助線。直径ＡＢに対する円周角から∠ＡＱＢ＝90°
△ＡＢＱは30°―60°―90°→辺の比が１：２：√３の有名三角形である。
【ＡＢ→ＱＢ→ＳＢ】
ＳＢ＝４×√３/２×√２＝２√６ｃｍ
え…２、お…６

大問５（空間図形）

（１）

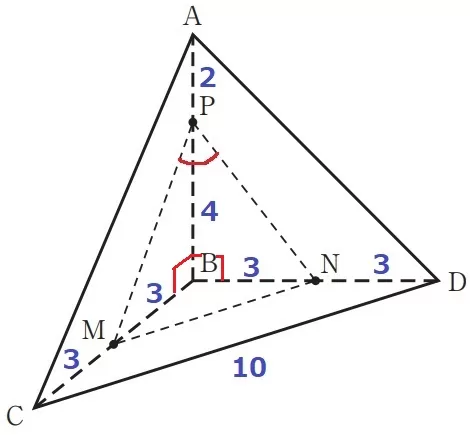
∠ＭＰＮを調べるには△ＰＭＮの特徴をつかむ。
∠ＣＢＤ≠90°に注意！

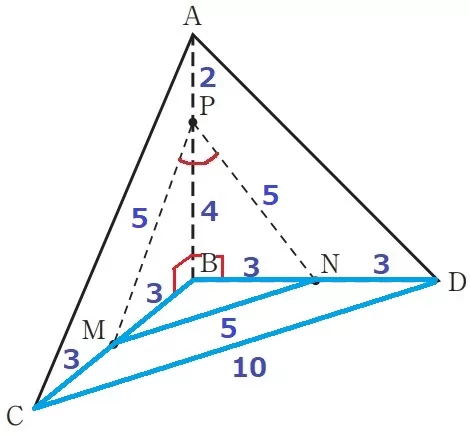
△ＰＭＢと△ＰＮＢは３：４：５の直角三角形→ＰＭ＝ＰＮ＝５ｃｍ
△ＢＭＮ∽△ＢＣＤより、ＭＮ＝10÷２＝５ｃｍ
△ＰＭＮは３辺が５ｃｍの正三角形→∠ＭＰＮ＝60°
か…６、き…０

（２）

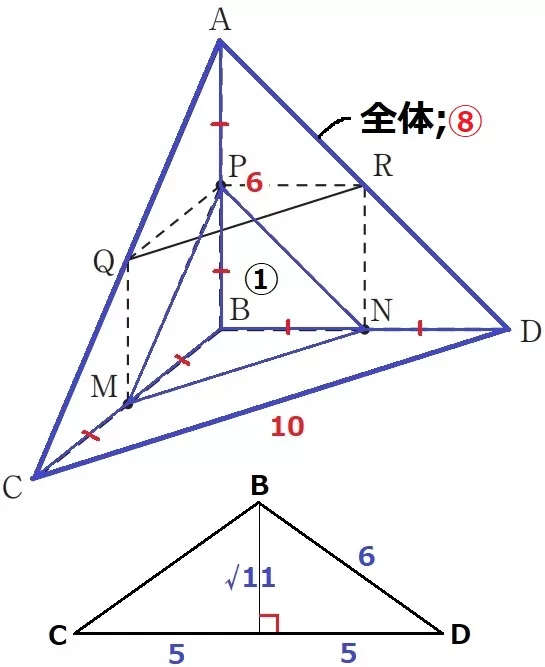
体積を求めるので、まず全体の三角錐Ａ―ＢＣＤを出せるようにしておく。
底面の△ＢＣＤは等辺が６ｃｍ、底辺が10ｃｍの二等辺三角形。
→半分に割って三平方を使うと高さは√11ｃｍ。

また、Ｐ・Ｍ・Ｎはそれぞれの辺の中点なので、
三角錐の体積比は、Ｂ―ＰＭＮ：Ｂ―ＡＣＤ＝①：⑧

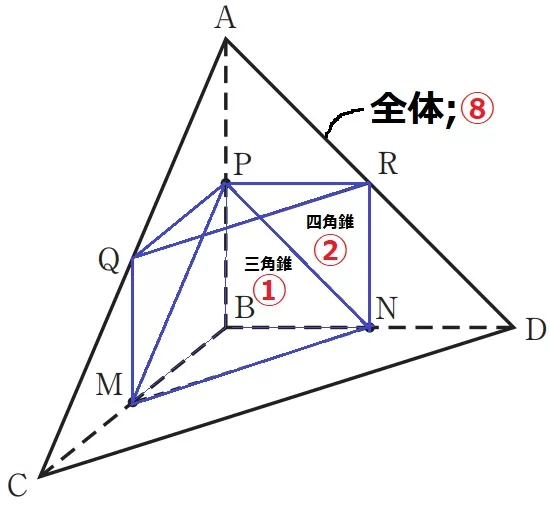
ここで、三角柱ＰＱＲ―ＢＭＮに着目する。
【柱÷３＝錘】
三角柱の体積を③とすると、三角錐Ｐ―ＢＭＮは①。
ということは、求積すべき四角錘Ｐ―ＭＮＲＱの体積は②にあたる。
したがって、10×√11÷２×６÷３×②/⑧＝５√11/２ｃｍ³
く…５、け…１、こ…１、さ…２
公立高校入試解説ページに戻る