問題ＰＤＦ
【図１】のように、正十二角形ＡＢＣＤＥＦＧＨＩＪＫＬがあり、
対角線ＡＧの中点をＯとするとき、ＯＡ＝１ｃｍである。このとき、次の問いに答えなさい。
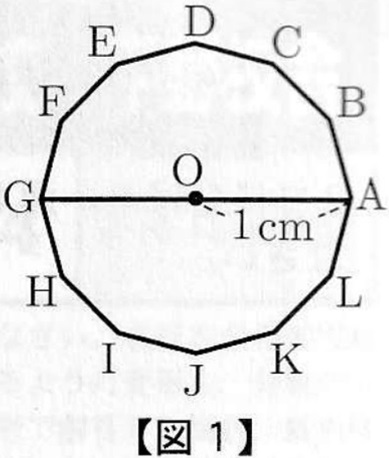
（１）
△ＯＡＢの面積を求めなさい。
（２）
【図２】は、【図１】の正十二角形に点Ａを中心として線分ＡＤの長さを半径とする円を
かき加えたものである。影をつけた部分の面積を求めなさい。
（３）
【図３】は、【図１】の正十二角形に点Ａを中心として、線分ＡＣ、ＡＤ、ＡＥの長さを半径とする３つの円を
かき加えたものである。影をつけた部分の面積の和を求めなさい。
＠解説＠
（１）
∠ＢＯＡ＝360÷12＝30°
Ｂから垂線をひくと、辺の比が１：２：√３の直角三角形があらわれる。
△ＯＡＢの底辺をＯＡとしたときの高さは、１÷２＝１/２ｃｍ
△ＯＡＢの面積は、１×１/２÷２＝１/４ｃｍ2
（２）
曲線ＤＪを弧とする扇形をつくる。
Ａ・Ｄ・Ｇ・Ｊは正十二角形の頂点２個飛ばし。
回転対称から四角形ＡＤＧＪは正方形→∠ＤＡＪ＝90°
Ｏを復元すると、直角三角形ＯＡＤの辺の比１：１：√２から半径ＡＤ＝√２ｃｍ
扇形ＡＤＪの面積は、√２×√２×π×１/４＝π/２ｃｍ2
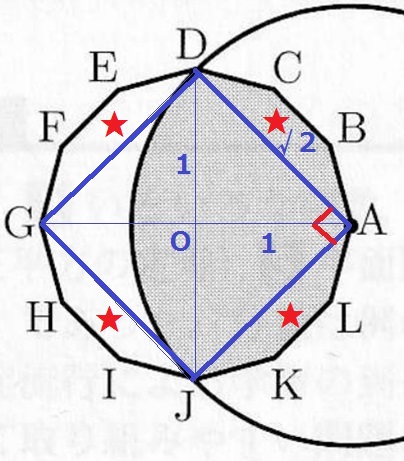
残りの部分は正十二角形から正方形ＡＤＧＪをひいて★×４、これを÷２をすると★×２になる。
正十二角形の面積は、（１）の△ＯＡＢ12個分で１/４×12＝３ｃｍ2
★×２＝｛３－（√２）2｝÷２＝１/２ｃｍ2
したがって、求積すべき図形の面積は、π/２＋１/２＝（π＋１）/２ｃｍ2
（３）
なんかもうヤバイし、ずっと見てると気分悪くなってくる(´Д`||)
正解者はほとんどいないと思うので本番では捨てましょう。
曲線は扇形の弧にしないと求まらないので、扇形ＡＥＩを作図する。
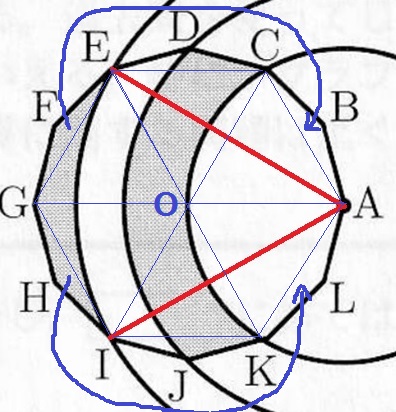
正六角形ＡＣＥＧＩＫを６分割した正三角形を描いてみた。
左が曲者なので、△ＥＦＧと△ＧＨＩを△ＡＢＣと△ＫＬＡへお引越し。
それぞれ正十二角形の１辺を等辺とする合同な二等辺三角形である。
★２つに狙いを定める。
小さい正三角形の１辺は１ｃｍ。その高さは√３/２ｃｍで、ＡＥ＝√３/２×２＝√３ｃｍ
△ＡＥＩは正十二角形の頂点３個飛ばしだから正三角形。∠ＥＡＩ＝60°、ＥＩ＝√３ｃｍ
ＡＧ＝２ｃｍで、ＡＧとＥＩは直交する。
★×２＝四角形ＡＥＧＩ－扇形ＡＥＩ
＝２×√３÷２－√３×√３×π×１/６
＝√３－π/２ｃｍ2
★は先ほど求めたところ。
残りの部分は（２）で求めた図形から扇形ＡＣＫを引けばいい。
（π＋１）/２－１×１×π×１/３
＝（π＋３）/６
したがって、求積すべき図形の面積は、
√３－π/２＋（π＋３）/６
＝１/２＋√３－π/３ｃｍ2
国私立高校入試解説ページに戻る
コメント