2020年度　慶應義塾高校過去問【数学】大問６解説

問題ＰＤＦ
下の図は、１辺の長さ６ａの正多角形の面のみでできた立体の展開図である。

完成した立体の表面に沿って点Ｐと点Ｑを最短経路でつないだとき、
最短距離の長さを求めよ。

＠解説＠
難問です。
幾何に卓抜している人以外はスルー推奨…。

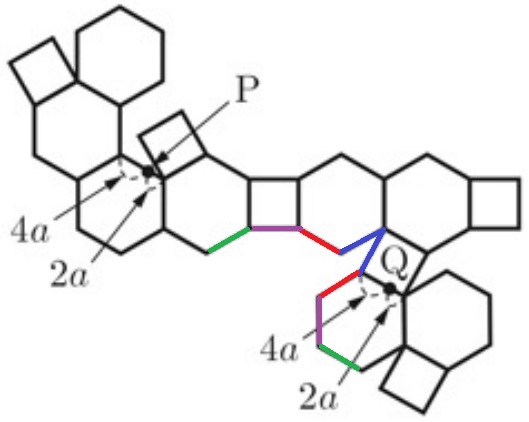
ＰＱが最短となる位置関係を探るが…ＰとＱが離れていて辛い(-_-;)
接する辺に注意してＰをＱ側へ寄せてみる。

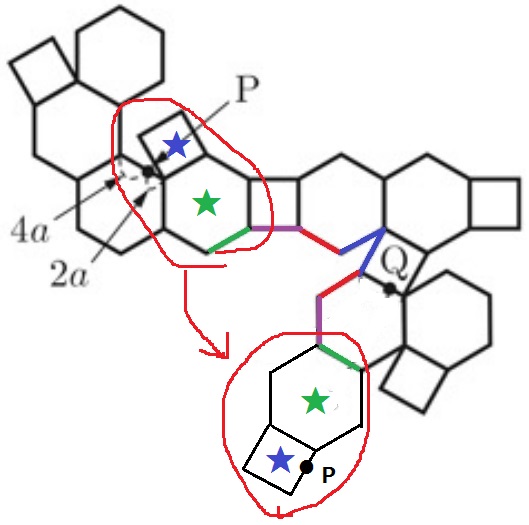
Ｐは正方形★の辺上の点でもある。
正方形★と正六角形★の２つだけを右下へ移動してみた。

しかし、これで満足してはならぬ( ‘д’⊂彡☆))Д´) ﾊﾟｰﾝ
まだＰを近くに寄せられるか検証する。

展開図に目を凝らすと、正方形の４辺それぞれに別々の正六角形がくっつく構図になっている。
そこで、正方形の右側に正六角形を新調し、こちらに点Ｐを移動してみる。
すると右図のようになる。さっきよりＰＱが短くなったような気がする…。

さらに、Ｐがある正六角形を左上に傾け、３つの正六角形でＰＱをとらえることも出来る。
これ以外はないはず。マジで面倒くさい。

整理。
どれが一番短いでしょうか？⊂(^ω^)⊃

いちいち全部の長さを求める時間はないので感覚も必要。
【１】はＱＲ＝２ａ、ＰＲは２ａ＋正六角形の高さ２つ分。
【３】のＰＲにも正六角形の高さ２つ分が含まれるが、
細かく分析すると剰余の長さが２ａ未満（青線が２ａ）。
ＱＲは２ａを超えるが、ＱＲよりＰＲを短くとった方がＰＱが短くなる。
【３】の方が短い（はず）。

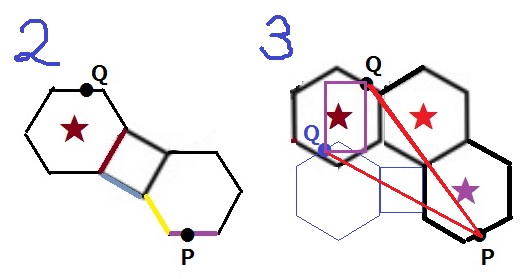
【２】と【３】を比較。
【３】の図に【２】を写すと視覚的に【２】の方が短い。
２つのＱを通る長方形を描くと縦長になり、【２】のＱがＰに近いと思う。

■追記■

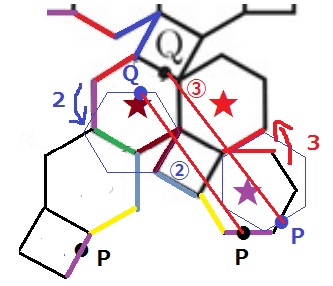
こっちの比較のほうがわかりやすいかな？
③より②が短い。
ということで、【２】を選択します(*´ｪ`*)

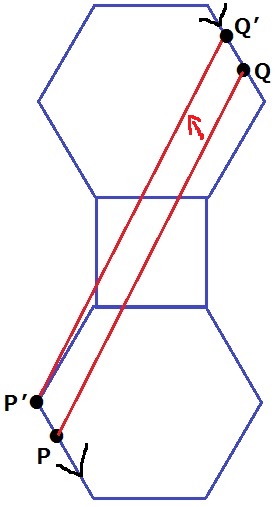
ここまでたどりつけても難所はつづく。。
２つの正六角形の辺が平行であることを利用して、Ｐを正六角形の頂点に移動。
ＰＱの移動先をＰ’Ｑ’とおく。

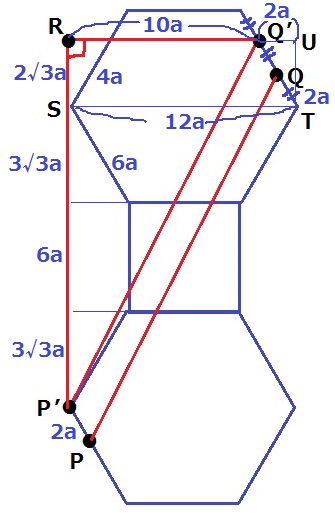
ＳＴは正六角形の対角線で12ａ。
Ｑ’Ｔ＝４ａ
直角三角形Ｑ’ＵＴは内角が30°－60°－90°→辺の比が１：２：√３でＱ’Ｕ＝２ａ
ＲＱ’＝ＳＴ－Ｑ’Ｕ＝12ａ－２ａ＝10ａ
ＲＰ’は１：２：√３の直角三角形３つと正方形の１辺を合計して（６＋８√３）ａ。

最後に計算だが、この三平方もシビア・ﾟ・(ﾟ｀Д´ﾟ)・ﾟ・

解答は二重根号の形になります。
最後のａはルートに含みません。328と96はともに４の倍数なのでルートの右側は２。
ＰＱ＝２√（82＋24√３）ａ
ところで何名正解できたワケ？(#^ω^)????

＠余談＠

パラメトロン計算機より。
本問の図形は切頂八面体といって、正八面体の頂点を切り落としてできる図形です。

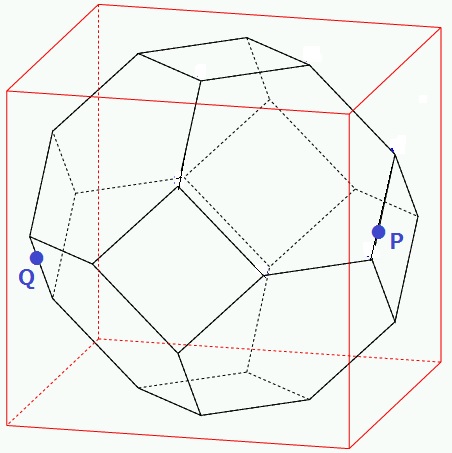
↑Ｐ・Ｑを空間で示すとこんな位置関係。
国私立高校入試解説ページに戻る