問題PDF
(1)
2次方程式x2-5x-3=0の正の解の小数部分をaとするとき、
a(a+5)の値を求めなさい。
(2)
2m-1≦√m≦2mを満たす自然数nが2020個あるとき、
自然数mの値を求めなさい。
(3)
大小2つのさいころを振り、出た目をそれぞれa、bとします。
このとき、11a+8bの値が7の倍数となる確率を求めなさい。
(4)

上の図のように、平行四辺形ABCDの辺AB、BC、CD、DAを2:3に分ける点をそれぞれE、F、G、Hとします。線分AFと線分ED、BGの交点をそれぞれP、Qとし、線分HCと線分BG、EDの交点をそれぞれR、Sとします。このとき、四角形PQRSの面積は平行四辺形ABCDの面積の何倍ですか。
@解説@
(1)
x2-5x-3=0に解の公式を適用。
x=(5±√37)/2
まず、√37の整数部分を考える。
√36<√37<√49だから、√37の整数部分は6。
5より√37の方が大きいので、『正の解』は(5+√37)/2
(5+√37)/2の整数部分は、(5+6…)÷2=11…÷2=5…
小数部分a=正の解-整数部分=(5+√37)/2-5
a(a+5)
={(5+√37)/2-5}{(5+√37)/2-5+5}
={(√37-5)/2}{(√37+5)/2}
={(√37)2-52}/4=12/4=3
(2)
2m-1≦√n≦2m ←2乗
(2m-1)2≦n≦(2m)2
2m-1と2mは連続する整数。
連続する2つの整数の平方数のあいだにある数を考えればいい。
留意すべきは、不等号≦にイコールがあること。
つまり、(2m-1)2もnに含まれる。
(たとえば、4と9の差は9-4=5個だが、4を含めると5+1=6個となる)
n=2020は(2m-1)2を含む個数なので、(2m)2と(2m-1)2の差は2019。
(2m)2-(2m-1)2=2019
4m2-4m2+4m-1=2019
4m=2020
m=505
(3)
7の倍数の判定法は使えにくい。
地道に代入して調べていくが、余りに注目しよう。
11=7+4(余り4)
8=7+1(余り1)
余りの合計が7の倍数であれば全体で7の倍数。
たとえば、a=1のとき、余り4×1+余り1×3=7だからb=3となる。
a=2のとき、4×2+1×6=14→b=6
a=3のとき、4×3+1×2=14→b=2
a=4のとき、4×4+1×5=21→b=5
a=5のとき、4×5+1×1=21→b=1
a=6のとき、4×6+1×4=28→b=4
以上、6通り→6/36=1/6
(4)
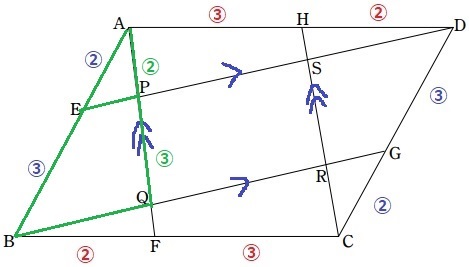
平行四辺形は対辺の長さが等しく、辺を内分する比が同じ。
AF//HC、ED//BG
△AEP∽△ABQより、AP:PQ=AE:EB=2:3

△ADP∽△HDSに注目。
HS=②×2/5=〇4/5
図形全体が点対称なので、対称的に考えてQF=〇4/5
分数がでてきたので、いったん比を整数に変換する。
AP:PQ:QF=②:③:〇4/5=⑩:⑮:④
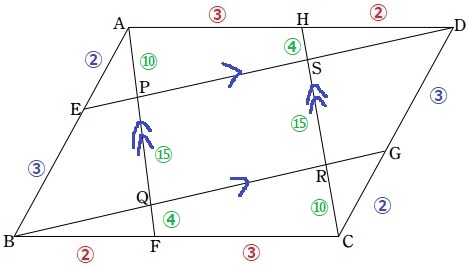
平行四辺形ABCDの面積を1として、上底+下底の和から面積比を計算する。
【平行四辺形ABCD→平行四辺形AFCH→四角形PQRS】
1×6/10×30/58=9/29
9/29倍



コメント