問題ＰＤＦ
（１）
を計算せよ。
（２）
２次方程式
を解け。
（３）
１から６までの目の出る大小１つずつのさいころを同時に１回投げる。
大きいさいころの出た目の数をａ、小さいさいころの出た目の数をｂとするとき、
ａ√ｂ＜４となる確率を求めよ。ただし、大小２つのさいころはともに、
１から６までのどの目が出ることも同様に確からしいものとする。
（４）
下の表は、ある中学校の生徒40人が行ったゲームの得点をまとめたものである。
得点の中央値が12.5点であるとき、ｘ、ｙの値を求めよ。
（５）
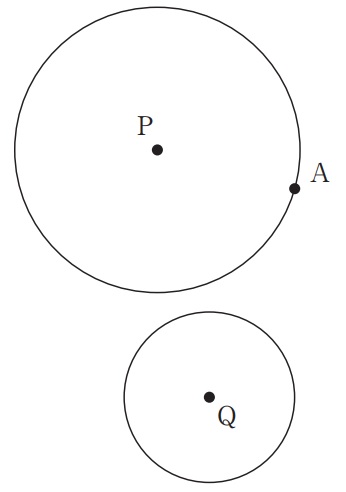
下の図のように、円Ｐと円Ｑは互いに交点をもたず、円Ｐの周上に点Ａがある。
点Ａにおいて円Ｐに接し、かつ円Ｑにも接するような円の中心のうち、
円Ｐおよび円Ｑの外部にある円の中心Ｏを、定規とコンパスを用いて作図によって求め、
中心Ｏの位置を示す文字Ｏを書け。ただし、作図に用いた線は消さないでおくこと。
＠解説＠
（１）
分母の（６－２√５）を２でくくると（３－√５）が現れて約分ができる。
３√２/４
（２）
初手は両辺を６倍。
＋２（３－２ｘ）の符号をいじると、－２（２ｘ－３）に変わる。
（カッコ外の２にマイナスをかけると、カッコ内の項が入れ替わる）
Ｘ＝２ｘ－３に置き換えて因数分解。最後は共通因数２でくくる。
ｘ＝４/３、２
（３）
√ｂの最小値√１＝１
ａ√ｂ＜４が成り立つａは４未満に限られる。（４×１＝４は×）
●ａ＝１
√ｂの最大値√６、２＜√６＜３
√６の整数部分は２なので、ｂ＝６でも１×√６＜４が成り立つ。
ｂ＝１～６の６通り。
●ａ＝２
√ｂ＜２＝√４であればいい。
ｂ＝１～３の３通り。
●ａ＝３
ｂ＝１→３×１＝３ ＯＫ！
ｂ＝２→√２＝1.41421356…（一夜一夜に人見ごろ）
３×1.41＝4.23でＮＧ！
１通り
計10通り。
全体は６×６＝36通りだから、確率は10/36＝５/18
（４）
40人の中央値は20番目と21番目の平均。
得点が５点刻みで平均が12.5点ということは、
上から20番目は15点、21番目は10点である。
（５と20の平均も12.5だが、10点がいるのであり得ない）
15点以上が20人なので、ｙ＝20－11＝９
ｘ＝40－（２＋３＋９＋11）＝15
ｘ＝15、ｙ＝９
（５）
西の作図は難しい(;´･ω･)
『点Ａにおいて円Ｐと接する』
半径と接線は直交する。
ＰＡとＡＯは一直線になる→円の中心Ｏは半直線ＰＡ上にある。
大問題は『円Ｑに接する』をどう対処すべきか…。
結果から方針を立ててみる。
仮に円QがＢで接すると、半径からＡＯ＝ＢＯ
Ｂは所在不明ゆえ頼れないが、ＢはＱＯ上にある。
ＱＯの距離を半直線ＰＡ上に移した交点をＱ’とする。
同様に半径からＱ’Ｏ＝ＱＯ
ＡＯ、ＢＯの長さはわからないが、円Ｑの半径をＡからとればＱ’の位置がわかる。
あとは２点Ｑ、Ｑ’を通る円の作図の問題で、ＱＱ’の垂直二等分線上にＯがある。
①半直線ＰＡをひく。
②Ａから円Ｑの半径をとる。
③上の交点とＱの垂直二等分線をひく。
①と③の交点がＯとなる。
国私立高校入試解説ページに戻る
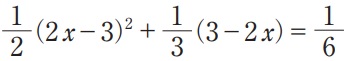
コメント