問題PDF
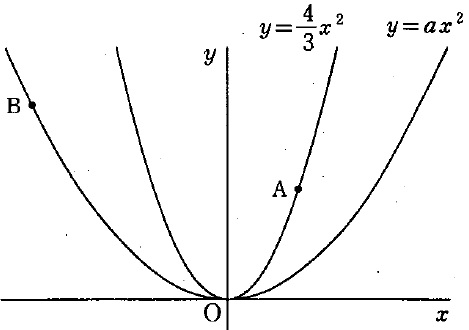
下の図のように、原点Oと、関数y=4/3x2のグラフ上に点Aが、関数y=ax2のグラフ上に点Bがあり、点Aのx座標は5/4、点Bのx座標は-3である。また、y=ax2について、xの値が-3から0まで増加するときの変化の割合は-1である。
①
点Aのy座標とaの値を求めよ。
②
関数y=ax2のグラフ上に点Cを、x座標とy座標の和が10/3となるようにとる。
このとき、点Cの座標を求めなさい。ただし、点Cのx座標は正とする。
③(1)
②のとき、△OACを点Aを回転の中心として180°だけ回転移動した図形を△O’AC’とする。
ここで、点Oに対応する点がO’、点Cに対応する点がC’である。
直線O’C’と直線OBとの交点をDとするとき、点Dのx座標を求めよ。
(2)y軸上に点Eを、△BDC’と△O’C’Eの面積が等しくなるようにとるとき、
点Eのy座標を求めよ。ただし、点Eのy座標は正とする。
@解説@
①
うしろの設問の前提となるので必答です。
y=4/3x2にx=5/4を代入。
y=4/3×(5/4)2=25/12
y=ax2にグラフでxの値がp→qに増加したときに変化の割合はa(p+q)
a(-3+0)=-1
a=1/3
点Aのy座標…25/12、a=1/3
②
解答では途中式も記述する。
Cのx座標をtとする。C(t、1/3t2)
t+1/3t2=10/3
t2+3t-10
=(t+5)(t-2)=0
t>0だから、t=2
y=1/3×22=4/3
C(2、4/3)
③(1)
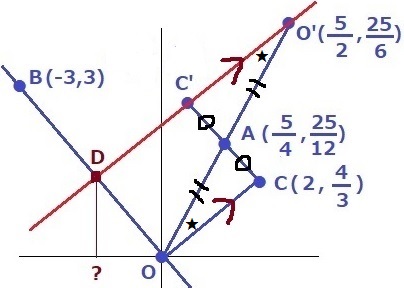
△OAC=△O’AC’、対応する角より∠AOC=∠AO’C’
錯角が等しく、OC//C’O’
OCの傾きは、4/3÷2=2/3
→C’O’の傾きも2/3
対応する辺よりOA=AO’だから、
O’の座標はA座標を2倍した(5/2、25/6)
C’O’は傾き2/3でO’(5/2、25/6)を通る直線なので、
25/6=2/3×5/2+b
b=5/2
C’O’;y=2/3x+5/2
B(-3、3)→BO;y=-x
Dはy=2/3x+5/2とy=-xの交点。
2/3x+5/2=-x
x=-3/2
(2)
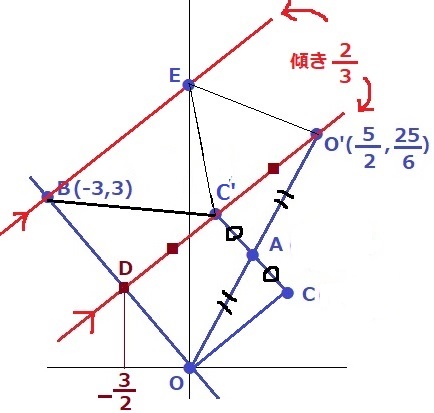
DC’とC’Oのx座標の差はともに2
C’はDO’の中点である。
これさえわかれば、△BDC’と△O’C’Eにおいて底辺はDC’=C’O’だから、
高さが等しい→平行線
Bを通るDO’に平行な線を描き、y軸との交点がEとなる。
BEの傾きは2/3。
Bから右に3、上に2移動してE(0、5)
Eのy座標は5。



コメント